Lý Thuyết Hàm Số Bậc Hai | SGK Toán Lớp 10
Có thể bạn quan tâm
1. Hàm số bậc hai
Định nghĩa
Hàm số bậc hai được cho bởi công thức:
\[y = ax^2 + bx + c (a ≠ 0)\]
có tập xác định \(D =\mathbb R\) và biệt thức \(\Delta = {b^2} - 4ac\)
Chiều biến thiên:
Nếu \(a > 0\) thì hàm số \(y = a{x^2} + bx + c\):
+) Nghịch biến trên khoảng \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\)
+) Đồng biến trên khoảng \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\)
Hàm số đạt có điểm cực tiểu là \(\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Nếu \(a < 0\) thì hàm số \(y = a{x^2} + bx + c\):
+) Đồng biến trên khoảng \(\left( { - \infty ; - \dfrac{b}{{2a}}} \right)\)
+) Nghịch biến trên khoảng \(\left( { - \dfrac{b}{{2a}}; + \infty } \right)\)
Hàm số đạt có điểm cực đại là \(\left( {\frac{{ - b}}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
Bảng biến thiên:
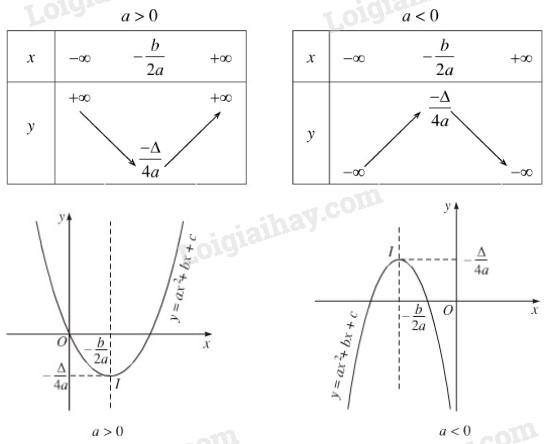
2. Đồ thị hàm số bậc hai
Đồ thị hàm số \(y = ax^2+ bx + c (a ≠ 0)\) là đường parabol có:
+) đỉnh là điểm \(I\left( { - \dfrac{b}{2a}; - \dfrac{\Delta }{4a}} \right)\)
+) trục đối xứng là đường thẳng \(x = - \dfrac{b}{2a}\).
+) Bề lõm của Parabol quay lên trên nếu \(a > 0\) và xuống dưới nếu \(a < 0\).
+) Giao điểm với trục tung: \(A(0; c)\).
+) Hoành độ giao điểm với trục hoành (nếu có) là nghiệm của phương trình \(ax^2 + bx + c = 0\).
* Cách vẽ
Cách 1: (Dùng cho mọi trường hợp)
Bước 1: Xác định tọa độ đỉnh I
Bước 2: Vẽ trục đối xứng
Bước 3: Xác định tọa độ các giao điểm của Parabol cới trục tung và trục hoành (nếu có)
Bước 4: Vẽ parabol (lưu ý dấu của hệ số a - liên quan đến bề lõm của Parabol)
Cách 2: (sử dụng khi đã có đồ thị hàm số \(y = ax^2\))
Đồ thị hàm số \(y = ax^2 + bx + c (a ≠ 0)\) suy ra từ đồ thị hàm số \(y = ax^2\) bằng cách:
+ Tịnh tiến song song với trục hoành \(\left| \dfrac{b}{2a} \right|\) đơn vị về bên trái nếu \(\dfrac{b}{2a}\) > 0, về bên phải nếu \(\dfrac{b}{2a}\) < 0.
+ Tịnh tiến song song với trục tung \(\left| - \dfrac{\Delta }{4a} \right|\) đơn vị lên trên nếu \( - \dfrac{\Delta }{4a}\) > 0, và xuống dưới nếu \( - \dfrac{\Delta }{4a}\) < 0.
Loigiaihay.com
Từ khóa » đỉnh Parabol Bậc 2
-
Hàm Số Bậc 2 Và Ứng Dụng Trong Giải Toán. - Kiến Guru
-
Toán 10 - Khảo Sát Hàm Số Bậc 2, Bài Tập áp Dụng - HayHocHoi
-
Bài 3. Hàm Số Bậc Hai - Củng Cố Kiến Thức
-
Cách Vẽ đồ Thị Hàm Số Bậc 2 ở Lớp 10 - Toán Thầy Định
-
Bài 3. Hàm Số Bậc Hai
-
Hàm Số Bậc 2 Là Gì? Cách Vẽ đồ Thị Và Một Số Bài Toán Thường Gặp
-
Xác định Hàm Số Bậc Hai
-
Hàm Số Bậc Hai Là Gì? Cách Vẽ đồ Thị Hàm Số Bậc Hai Lớp 9, Lớp 10
-
Lý Thuyết Hàm Số Bậc 2: Tính Biến Thiên Và đồ Thị Hàm Số
-
Hàm Số Bậc Hai - Lý Thuyết Và Các Bài Tập Liên Quan
-
Lý Thuyết Hàm Số Bậc Hai Môn Toán Lớp 10
-
Dạng 1: Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Hàm Số Bậc Hai - 7scv
-
Phương Trình Parabol Có Dạng Gì, Hàm Số Bậc 2 Và Ứng Dụng ...