Toán 10 - Khảo Sát Hàm Số Bậc 2, Bài Tập áp Dụng - HayHocHoi
Có thể bạn quan tâm
Tuy nhiên cũng còn khá nhiều em chưa hiểu rõ và nhớ được các bước khảo sát hàm số bậc 2, trong bài viết này sẽ hướng dẫn chi tiết các bước khảo sát hàm bậc 2, vận dụng vào bài tập để các em hiểu rõ hơn.
I. Khảo sát hàm số bậc hai y = ax2 + bx + c (a ≠ 0):
• TXĐ : D = R.
• Tọa độ đỉnh I (-b/2a; f(-b/2a)). f(-b/2a) = -Δ/4a
• Trục đối xứng : x = -b/2a
• Tính biến thiên :
a > 0 hàm số nghịch biến trên (-∞; -b/2a). và đồng biến trên khoảng (-b/2a; +∞)
a < 0 hàm số đồng biến trên (-∞; -b/2a). và nghịch biến trên khoảng (-b/2a; +∞)
- Bảng biến thiên :
* a > 0
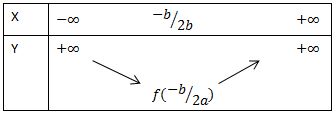
* a < 0

• Đồ thị:
- Đồ thị hàm số ax 2 + bx + c là một đường parabol (P) có: Đỉnh I (-b/2a; f(-b/2a)).
- Trục đối xứng : x = -b/2a. Parabol (P) quay bề lõm lên trên nếu a > 0, parabol (P) quay bề lõm xuống dưới nếu a < 0.

II. Bài tập áp dụng Khảo sát hàm số bậc 2
* Ví dụ 1 (Bài 2 trang 49 SGK Toán 10 CB): Lập bảng biến thiên và vẽ đồ thị hàm số:
a) y = 3x2 – 4x + 1
d) y = -x2 + 4x – 4
* Lời giải:
a) y = 3x2 – 4x + 1 ( a = 3; b =-4; c = 1)
TXĐ : D = R.
Tọa độ đỉnh I (2/3; -1/3).
Trục đối xứng : x = 2/3
Tính biến thiên :
a = 3 > 0 hàm số nghịch biến trên (-∞; 2/3). và đồng biến trên khoảng 2/3 ; +∞)
bảng biến thiên :
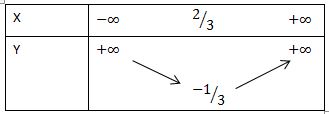 (P) giao trục hoành y = 0 : 3x2 – 4x + 1 = 0 <=> x = 1 v x = ½ Các điểm đặc biệt :
(P) giao trục hoành y = 0 : 3x2 – 4x + 1 = 0 <=> x = 1 v x = ½ Các điểm đặc biệt :
(P) giao trục tung : x = 0 => y = 1
Đồ thị :
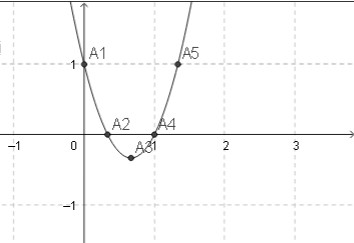
Đồ thị hàm số y = 3x2 – 4x + 1 là một đường parabol (P) có:
- Đỉnh I(2/3; -1/3).
- Trục đối xứng : x = 2/3.
- parabol (P) quay bề lõm lên trên .
d) y = -x2 + 4x – 4
TXĐ : D = R.
Tọa độ đỉnh I (2; 0).
Trục đối xứng : x = 2
Tính biến thiên :
a = -1 < 0 hàm số đồng biến trên (-∞; 2). và nghịch biến trên khoảng 2 ; +∞)
bảng biến thiên :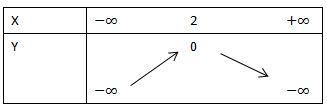 Các điểm đặc biệt :
Các điểm đặc biệt :
(P) giao trục hoành y = 0 : -x2 + 4x – 4 = 0 <=> x = 2
(P) giao trục tung : x = 0 => y = -4
Đồ thị :
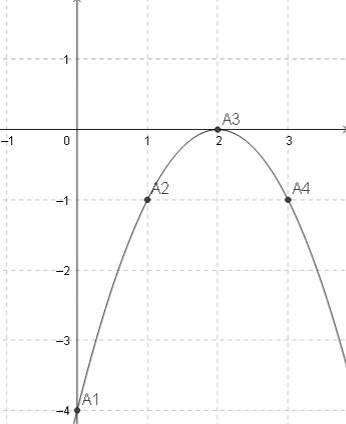
Đồ thị hàm số y = -x2 + 4x – 4 là một đường parabol (P) có:
- Đỉnh I(2; 0).
- Trục đối xứng : x = 2.
parabol (P) quay bề lõm xuống dưới .
* Ví dụ 2: Cho hàm số :y = f(x) = ax2 + 2x – 7 (P).
Tìm a để đồ thị (P) đi qua A(1, -2)
* Lời giải:
Ta có : A(1, -2) ∈(P), nên : -2 = a.12 + 2.1 – 7 ⇔ a = 3
Vậy : y = f(x) = 3x2 + 2x – 7 (P)
* Ví dụ 3: Cho hàm số :y = f(x) = ax2 + bx + c (P).
Tìm a, b, c để đồ thị (P) đi qua A(-1, 4) và có đỉnh S(-2, -1).
* Lời giải:
Ta có : A(-1, 4) ∈ (P), nên : 4 = a – b + c (1)
Ta có : S(-2, -1) ∈ (P), nên : -1 = 4a – 2b + c (2)
(P) có đỉnh S(-2, -1), nên : xS = -b/2a ⇔ 4a – b = 0 (3)
Từ (1), (2) và (3), ta có hệ : a-b+c=4 và 4a-2b+c=-1 và 4a-b=0
Giải hệ này được: a=5; b=20; c=19
Vậy : y = f(x) = 5x2 + 20x + 19 (P)
III. Bài tập khảo sát hàm số bậc 2 tự giải
* BÀI 1 : cho hàm số bậc hai : y = f(x) = x2 + 2mx + 2m – 1 (Pm). đường thẳng (d) : y = 2x – 3
a) Khảo sát và vẽ đồ thị của hàm số khi m = 2.
b) Tìm m để (Pm) tiếp xúc (d).
c) Tìm m để (d) cắt (Pm) tại hai điểm A, B phân biệt sao cho tam giác OAB vuông tại O.
* BÀI 2 : Cho hàm số :y = f(x) = ax2 + bx + 3 (P). tìm phương trình (P) :
a) (P) đi qua hai điểm A(1, 0) và B(2, 5).
b) (P) tiếp xúc trục hoành tại x = -1.
c) (P) đi qua điểm M(-1, 9) và có trục đối xứng là x = -2.
* BÀI 3 : Cho hàm số y = f(x) = x2 – 4|x|, (P)
a) Khảo sát và vẽ đồ thị của hàm số (P).
b) Tìm m để phương trình sau có 4 nghiệm : x2 – 4|x| + 2m – 3 = 0.
* Bài 4 : Cho hàm số: y = f(x) = -2x2 +4x – 2 (P) và (D) : y = x + m.
a) Khảo sát và vẽ đồ thị của hàm số (P).
b) Xác định m để (d) cắt (P) tại hai điểm phân biệt A và B thỏa AB = 2.
Từ khóa » đỉnh Parabol Bậc 2
-
Hàm Số Bậc 2 Và Ứng Dụng Trong Giải Toán. - Kiến Guru
-
Bài 3. Hàm Số Bậc Hai - Củng Cố Kiến Thức
-
Cách Vẽ đồ Thị Hàm Số Bậc 2 ở Lớp 10 - Toán Thầy Định
-
Bài 3. Hàm Số Bậc Hai
-
Hàm Số Bậc 2 Là Gì? Cách Vẽ đồ Thị Và Một Số Bài Toán Thường Gặp
-
Xác định Hàm Số Bậc Hai
-
Hàm Số Bậc Hai Là Gì? Cách Vẽ đồ Thị Hàm Số Bậc Hai Lớp 9, Lớp 10
-
Lý Thuyết Hàm Số Bậc 2: Tính Biến Thiên Và đồ Thị Hàm Số
-
Hàm Số Bậc Hai - Lý Thuyết Và Các Bài Tập Liên Quan
-
Lý Thuyết Hàm Số Bậc Hai Môn Toán Lớp 10
-
Lý Thuyết Hàm Số Bậc Hai | SGK Toán Lớp 10
-
Dạng 1: Khảo Sát Sự Biến Thiên Và Vẽ đồ Thị Hàm Số Bậc Hai - 7scv
-
Phương Trình Parabol Có Dạng Gì, Hàm Số Bậc 2 Và Ứng Dụng ...