Lý Thuyết Hàm Số Bậc Nhất Cần Nhớ - Abcdonline
Có thể bạn quan tâm
Công thức hàm số bậc nhất, tính chất hàm số bậc nhất, đồ thị hàm số bậc nhất, điều kiện để 2 đường thẳng song song, vuông góc.
Kiến thức cần nhớ:
1. Định nghĩa
+ Hàm số bậc nhất là hàm số được cho bởi công thức: ![]() trong đó
trong đó ![]()
![]()
![]()
![]()
![]()
![]() .
.
+ Khi ![]() thì hàm số bậc nhất trở thành hàm số
thì hàm số bậc nhất trở thành hàm số ![]() , biểu thị tương quan tỉ lệ thuận giữa
, biểu thị tương quan tỉ lệ thuận giữa ![]() và
và ![]() .
.
2. Tính chất
Hàm số bậc nhất, xác định với mọi giá trị ![]() .
.
Trên tập số thực, hàm số ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() và nghịch biến khi
và nghịch biến khi ![]() .
.
3. Đồ thị hàm số 






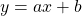
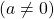
+ Đồ thị hàm số ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
+ ![]() gọi là hệ số góc của đường thẳng
gọi là hệ số góc của đường thẳng ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
4. Cách vẽ đồ thị hàm số 






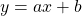
+ Vẽ hai điểm phân biệt của đồ thị rồi vẽ đường thẳng đi qua 2 điểm.
+ Thường vẽ đường thẳng đi qua 2 giao điểm của đồ thị với các trục tọa độ là ![]() .
.
+ Chú ý: Đường thẳng đi qua ![]() song song với trục tung có phương trình:
song song với trục tung có phương trình: ![]() , đường thẳng đi qua
, đường thẳng đi qua ![]() song song với trục hoành có phương trình:
song song với trục hoành có phương trình: ![]()
5. Kiến thức bổ sung
Trong mặt phẳng tọa độ cho hai điểm ![]() thì:
thì:
![]() .
.
Điểm ![]() là trung điểm của
là trung điểm của ![]() thì:
thì:
![]() .
.
6. Điều kiện để hai đường thẳng song song, hai đường thẳng vuông góc
Cho hai đường thẳng ![]() và đường thẳng
và đường thẳng ![]() với
với ![]() .
.
– Hai đường thẳng song song: ![]() và
và ![]() .
.
– Hai đường thẳng trùng nhau: ![]() và
và ![]() .
.
– Hai đường thẳng cắt nhau: ![]() cắt
cắt ![]() .
.
– Hai đường thẳng vuông góc: ![]()
*Chú ý: Gọi ![]() là góc tạo bởi đường thẳng
là góc tạo bởi đường thẳng ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , nếu
, nếu ![]() thì
thì ![]() .
.
Căn bậc hai, căn bậc ba, căn bậc n – Đại số 9
Sử dụng biểu thức phụ để tìm cực trị của biểu thức
Các dạng bài tập giải bài toán bằng cách lập phương trình, hệ phương trình
Biện luận nghiệm của phương trình bậc 2 bằng đồ thị
Cách chứng minh bất đẳng thức trong đề thi vào 10 môn Toán
Ví dụ giải hệ phương trình quy về bậc nhất
Hệ phương trình bậc nhất chứa tham số
Từ khóa » đặc điểm Của đồ Thị Hàm Số Bậc Nhất
-
Đồ Thị Của Hàm Số Bậc Nhất
-
HÀM SỐ BẬC NHẤT
-
Tổng Hợp Tất Cả Các Kiến Thức Về Hàm Số Bậc Nhất Và Dạng Bài Tập ...
-
Hàm Số Bậc Nhất – Wikipedia Tiếng Việt
-
Lý Thuyết đầy đủ Nhất Về Hàm Số Bậc Nhất - CungHocVui
-
Lý Thuyết đồ Thị Của Hàm Số Y = Ax + B (a ≠ 0). | SGK Toán Lớp 9
-
Phương Pháp Giải Các Dạng Toán Hàm Số Bậc Nhất Cơ Bản
-
Đồ Thị Của Hàm Số Bậc Nhất
-
Chuyên đề Hàm Số Và đồ Thị Bậc Nhất - Bậc Hai (khuyết)
-
Hàm Số Bậc Nhất - Lý Thuyết Và Phương Pháp Giải Bài Tập
-
Hàm Số Bậc Nhất - Lý Thuyết Toán 9
-
Định Nghĩa, Tính Chất Hàm Số Bậc Nhất - Đại Số 9 - Toán Lớp 9
-
Bài 3. Đồ Thị Hàm Số Y=ax+b