Lý Thuyết Nhân đơn Thức Với đa Thức (năm 2022 + Bài Tập) – Toán 8

Lý thuyết Toán 8 Bài 1: Nhân đơn thức với đa thức

Bài giảng Toán 8 Bài 1: Nhân đơn thức với đa thức

A. Lý thuyết.

Quy tắc: Muốn nhân một đơn thức với một đa thức, ta nhân đơn thức với từng hạng tử của đa thức rồi cộng các tích với nhau.

Tổng quát: Với A, B, C là các đơn thức, ta có: A.(B + C) = A.B + A.C.

Ví dụ:

3x.(x3 + 2x – 5) = 3x.x3 + 3x.2x – 3x.5 = 3x4 + 6x2 – 15x.

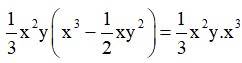
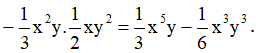
Chú ý: Ta thường sử dụng các phép toán liên quan đến lũy thừa sau khi thực hiện phép nhân:

Với m, n là các số tự nhiên, a ≠ 0, ta có:

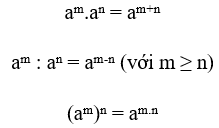
B. Bài tập tự luyện.

Bài 1: Rút gọn các biểu thức sau:

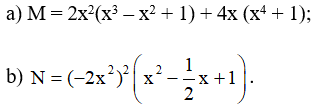
Lời giải:

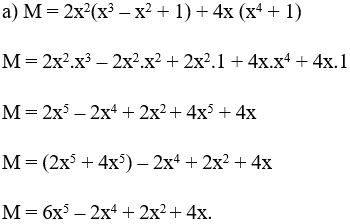
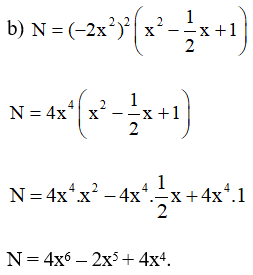
Bài 2: Thực hiện phép nhân, rút gọn rồi tính giá trị của biểu thức:

M = a (a – b) + b (a + b) – 5 tại a = 2; b = 1.

Lời giải:

M = a (a – b) + b (a + b) – 5

M = a.a – a.b + b.a + b.b – 5

M = a2 – a.b + b.a + b2 – 5

M = a2 + b2 – 5

Thay a = 2; b = 1 vào biểu thức M đã rút gọn ta được: M = 22 + 12 – 5 = 0.

Vậy giá trị của biểu thức M tại a = 2; b = 1 là 0.

Bài 3: Tìm x biết:

4x(8x + 5) – 16x(2x + 1) – 8 = 0.

Lời giải:

Ta có:

4x(8x + 5) – 16x(2x + 1) – 8 = 0

4x.8x + 4x.5 – 16x.2x – 16x. 1 – 8 = 0

32x2 + 20x – 32x2 – 16x – 8 = 0

(32x2 – 32x2) + (20x – 16x) – 8 = 0

4x – 8 = 0

4x = 8

x = 2

Vậy x = 2.

Trắc nghiệm Toán 8 Bài 1: Nhân đơn thức với đa thức

Bài 1: Rút gọn và tính giá trị của biểu thức

P = 5x2−[4x2−3x(x−2)] với x = −32

A. P = 4x2 – 6x. Với x = −32 thì P = 18

B. P = 4x2 + 6x. Với x = −32 thì P = 0

C. P = 4x2 – 6x. Với x = −32 thì P = -18

D. P = 4x2 + 6x. Với x = −32 thì P = 18

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có P = 5x2−[4x2−3x(x−2)]

= 5x2 – (4x2 – 3x2 + 6x)

= 5x2 – (x2 + 6x)

= 5x2 – x2 – 6x

= 4x2 – 6x

Thay x = vào biểu thức P = 4x2 – 6x ta được

P =4.(−32)2−6.(−32)=4.94+182=18

Vậy P = 4x2 – 6x. Với x = -32 thì P = 18

Bài 2: Kết quả của phép tính

(ax2 + bx – c).(– 4a2x) bằng

A. – 4a3x3 + 4a2bx2 + 4a2cx

B. 4a3x3 – 4a2bx2 – 4a2cx

C. 4a3x3 + 4a2bx2 – 4a2cx

D. – 4a3x3 – 4a2bx2 + 4a2cx

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

(ax2 + bx – c).(– 4a2x) = (– 4a2x).(ax2 + bx – c)

= (– 4a2x).ax2 + (– 4a2x).bx – (– 4a2x).c

= – 4a3x3 – 4a2bx2 + 4a2cx

Bài 3: Chọn câu sai.

A. Giá trị của biểu thức ax(ax + y) tại x = 1; y = 0 là a2.

B. Giá trị của biểu thức ay2(ax + y) tại x = 0; y = 1 là (1 + a)2.

C. Giá trị của biểu thức -xy(x - y) tại x = -5; y = -5 là 0.

D. Giá trị của biểu thức xy(-x - y) tại x = 5; y = -5 là 0.

Hiển thị đáp án

Đáp án: B

Giải thích:

+) Thay x = 1; y = 0 vào biểu thức ax(ax + y) ta được

a.1(a.1 + 0) = a.a = a2 nên phương án A đúng

+) Thay x = 0, y = 1 vào biểu thức ay2(ax + y) ta được

a.12(a.0 + 1) = a.1 = a nên phương án B sai.

+) Thay x = −5, y = −5 vào biểu thức −xy(x − y) ta được

−(−5)(−5)[−5 − (−5)] = −25.0 = 0 nên phương án C đúng

+) Thay x = 5, y = −5 vào biểu thức xy(−x − y) ta được

5.(−5)[−5 − (−5)] = −25.0 = 0 nên phương án D đúng.

Bài 4: Cho biểu thức C = x(y + z) – y(z + x) – z(x – y). Chọn khẳng định đúng.

A. Biểu thức C không phụ thuộc vào x; y; z

B. Biểu thức C phụ thuộc vào cả x; y; z

C. Biểu thức C chỉ phụ thuộc vào y

D. Biểu thức C chỉ phụ thuộc vào z

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có

C = x(y + z) – y(z + x) – z(x – y)

= xy + xz – yz – xy – zx + zy

= (xy – xy) + (zy – zy) + (xz – zx)

= 0

Nên C không phụ thuộc vào x; y; z

Bài 5: Cho biểu thức M = x2(3x – 2) + x(-3x2 + 1). Hãy chọn câu đúng

A. Giá trị của biểu thức M tại x = 0 là 1

B. Giá trị của biểu thức M tại x = 1 là 1

C. Giá trị của biểu thức M tại x = -2 là -6

D. Giá trị của biểu thức M tại x = 3 là -15

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có

M = x2(3x – 2) + x(-3x2 + 1)

= x2.3x + x2.(-2) + x.(-3x2) + x.1

= 3x3 – 2x2 – 3x3 + x

= -2x2 + x

Thay x = 0 vào M = -2x2 + x ta được

M = -2.02 + 0 = 0 nên A sai.

Thay x = 1 vào M = -2x2 + x ta được

M = -2.12 + 1 = -1 nên B sai

Thay x = -2 vào M = -2x2 + x ta được

M = -2.(-2)2 + (-2) = -10 nên C sai.

Thay x = 3 vào M = -2x2 + x ta được

M = -2.32 + 3 = -15 nên D đúng

Bài 6: Với mọi giá trị của x thì giá trị của biểu thức

−2x(3x − 1) + 6x(x + 1) + (3 −8x) là

A. 2

B. 3

C. 4

D. Một đáp số khác

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

−2x(3x − 1) + 6x(x + 1) + (3 −8x)

= − 6x2 + 2x + 6x2 + 6x + 3 − 8x

= (− 6x2 + 6x2) + (2x + 6x − 8x) + 3

= 0 + 0 + 3 = 0

Bài 7: Giá trị của biểu thức

5x(x − 4y) − 4y(y − 5x)

với x =−15, y =−12là:

A.−23

B.−34

C. −45

D.−56

Hiển thị đáp án

Đáp án: C

Giải thích:

Ta có: 5x(x − 4y) − 4y(y − 5x)

= 5x2−20xy−4y2+20xy

= 5x2 - 4y2

Thay x = −15, y = −12 vào biểu thức trên

ta được: 5.−152−4.−122=−45

Bài 8: Biểu thức rút gọn của biểu thức

3x3 + 7x2 − 3x(2x2 + 7x −1) là:

A. −3x3 + 14x2 + 3x

B. −3x3 − 14x2 + 3x

C. −x3 −14x2 − 3x

D. Một đáp số khác

Hiển thị đáp án

Đáp án: B

Giải thích:

Ta có:

3x3 + 7x2 − 3x(2x2 + 7x −1)

= 3x3 + 7x2 - 6x3 - 21x2 + 3x

= -3x3 - 14x2 + 3x

Bài 9: Biết 5(2x − 1) − 3(8 − 4x) = 59. Giá trị của x là:

A. 4

B. 4,5

C. 5

D. 5,5

Hiển thị đáp án

Đáp án: A

Giải thích:

Ta có: 5(2x − 1) − 3(8 − 4x) = 59

Suy ra

10x - 5 - 24 + 12x = 59

⇔10x + 12x = 59 + 5 + 24

⇔22x = 88

⇔x = 4

Bài 10: Tích 4a3b.(3ab−b+14) có kết quả bằng

A. 12a4b2 – 4a3b + a3b

B. 12a4b2 – 4a3b2 + a3b

C. 12a3b2 + 4a3b2 + 4a3b

D. 12a4b2 – 4a3b2 + a3b

Hiển thị đáp án

Đáp án: D

Giải thích:

Ta có:

4a3b.(3ab−b+14)

= 4a3b.3ab – 4a3b.b + 4a3b. 14

= 12a4b2 – 4a3b2 + a3b

Xem thêm các bài tổng hợp lý thuyết Toán lớp 8 đầy đủ, chi tiết khác:

Lý thuyết Nhân đa thức với đa thức

Lý thuyết Những hằng đẳng thức đáng nhớ

Lý thuyết Những hằng đẳng thức đáng nhớ (tiếp theo)

Lý thuyết Những hằng đẳng thức đáng nhớ (tiếp theo)

Lý thuyết Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung