Mệnh đề Là Gì? Mệnh đề Phủ định, Mệnh đề Kéo Theo Và Mệnh đề đảo

Vậy Mệnh đề là gì? các loại mệnh đề như: Phủ định mệnh đề, Mệnh đề kéo theo và Mệnh đề đảo được phát biểu như thế nào? chúng ta cùng tìm hiểu qua nội dung bài viết Mệnh đề dưới đây.

A. Lý thuyết Mệnh đề

I. Mệnh đề, mệnh đề chứa biến

1. Mệnh đề là gì?

- Mệnh đề là câu khẳng định có thể xác định được tính đúng hay sai. Một mệnh đề không thể vừa đúng, vừa sai.

* Ví dụ: Câu "π2 > 10" là một mệnh đề sai

2. Mệnh đề chứa biến là gì?

- Mệnh đề chứa biến là câu khẳng định mà sự đúng hay sai của nó còn tùy thuộc vào một hay nhiều yếu tố biến đổi.

* Ví dụ: Câu "Số nguyên n chia hết cho 5" không phải là mệnh đề, vì không thể xác định được nó đúng hay sai. Nhưng:

- Nếu ta gán cho n giá trị n = 8 thì ta có thể có một mệnh đề sai (vì 8 không chia hết cho 5).

- Nếu gán cho n giá trị n = 25 thì ta có một mệnh đề đúng.

II. Phủ định một mệnh đề

• Phủ định của một mệnh đề 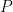, là một mệnh đề, kí hiệu là  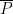. Hai mệnh đề  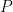và 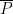 có những khẳng định trái ngược nhau, tức là:

 - Nếu 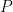 đúng th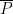ì  sai.

 - Nếu 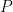 sai thì  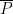đúng.

* Ví dụ: Cho mệnh đề 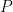: "6 là số nguyên tố".

→ Đây là mệnh đề SAI.

 Mệnh đề phủ định: "6 không là số nguyên tố"

→ Đây là mệnh đề ĐÚNG.

III. Mệnh đề kéo theo

• Mệnh đề kéo theo có dạng: "Nếu 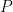 thì 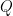 ", trong đó  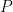và 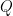 là hai mệnh đề. Mệnh đề "Nếu  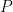thì 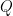" kí hiệu là P→Q. Tính đúng, sai của mệnh đề kéo theo như sau:

 - Mệnh đề P→Q chỉ sai khi 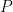 đúng và  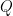sai.

* Ví dụ: Cho hai mệnh đề P :"5 chia hết cho 3" và Q:"6 là số chẵn"

- Khi đó P ⇒ Q phát biểu là: "Nếu 5 chia hết cho 3 thì 6 là số chẵn"

→ Đây là mệnh đề đúng vì P sai, Q đúng.

IV. Mệnh đề đảo - Mệnh đề tương đương

1. Mệnh đề đảo là gì?

 - Mệnh đề "Q ⇒ P" là mệnh đề đảo của mệnh đề "P ⇒ Q"

* Ví dụ: Trong ví dụ trên, mệnh đề Q ⇒ P phát biểu là: "Nếu 6 là số chẵn thì 5 chia hết cho 3"

→ Mệnh đề này sai vì Q đúng P sai.

2. Mệnh đề tương đương

- Nếu P ⇒ Q là một mệnh đề đúng và mệnh đề Q ⇒ P cũng là một mệnh đề đúng thì ta nói P tương đương với Q, kí hiệu: P ⇔ Q.

- Khi P ⇔ Q, ta cũng nói P là điều kiện cần và đủ để có Q hoặc P khi và chỉ khi Q hay Q nếu và chỉ nếu P.

* Ví dụ: Cho hai mệnh đề P:"6 chia hết cho 2" và Q:"4 là số chẵn"

- Khi đó mệnh đề P và Q đều đúng nên P ⇔ Q phát biểu là "6 chia hết cho 2 khi và chỉ khi 4 là số chẵn".

V. Ký hiệu ∀ và ký hiệu ∃

• Ký hiệu ∀ đọc là "với mọi"

• Ký hiệu ∃ đọc là "có một" (tồn tại một) hay "có ít nhất  một" (tồn tại ít nhất một).

• Cho mệnh đề chứa biến: P(x), trong đó x là biến nhận giá trị từ tập hợp X.

- Câu khẳng định: Với x bất kì thuộc X thì P(X) là mệnh đề đúng được kí hiệu là: ∀x ∈ X: P(x).

* Ví dụ: Câu " Bình phương của mọi số thực đều lớn hơn hoặc bằng 0" là một mệnh đề. Có thể viết mệnh đề này như sau: ∀x ∈ R: x2 ≥ 0 hay x2 ≥ 0, ∀x ∈ R

- Câu khẳng định: Có ít nhất một x thuộc X (hay tồn tại x thuộc X) để P(x) là mệnh đề đúng kí hiệu là: ∃x ∈ X: P(x).

* Ví dụ: Câu " Có mọt số nguyên nhỏ hơn 5" là một mệnh đề. Có thể viết mệnh đề này như sau: ∃n ∈ Z: n < 5.

B. Bài tập Mệnh đề

* Bài 1 trang 9 SGK Đại số 10: Trong các câu sau, câu nào là mệnh đề, câu nào là mệnh đề chứa biến?

a) 3 + 2 = 7 ;       b) 4 + x = 3;

c) x + y > 1 ;       d) 2 - √5 < 0

¤ Lời giải:

a) 3 + 2 = 7 là mệnh đề và là mệnh đề sai. Vì 3 + 2 = 5 ≠ 7

b) 4 + x = 3 là mệnh đề chứa biến. Vì với mỗi giá trị của x ta được một mệnh đề.

- Ví dụ : với x = 1 ta có mệnh đề " 4 + 1 = 3".

 với x = –1 ta có mệnh đề "4 + (–1) = 3".

 với x = 0 ta có mệnh đề "4 + 0 = 3".

c) x + y > 1 là mệnh đề chứa biến. Vì với mỗi cặp giá trị của x, y ta được một mệnh đề.

- Ví dụ : x = 0 ; y = 1 ta có mệnh đề « 0 + 1 > 1 »

 x = 1 ; y = 3 ta có mệnh đề « 1 + 3 > 1 ».

d) 2 – √5 < 0 là mệnh đề và là mệnh đề đúng. Vì 2 = √4 và √4 < √5.

* Bài 2 trang 9 SGK Đại số 10: Xét tính đúng sai của mỗi mệnh đề sau và phát biểu mệnh đề phủ định của nó:

a) 1794 chia hết cho 3 ;         b) √2 là một số hữu tỉ

c) π < 3, 15 ;         d) |-125| ≤ 0

¤ Lời giải:

a) Mệnh đề "1794 chia hết cho 3" đúng vì 1794 : 3 = 598

 Mệnh đề phủ định: "1794 không chia hết cho 3"

b) Mệnh đề "√2 là số hữu tỉ" sai vì √2 là số vô tỉ

 Mệnh đề phủ định: "√2 không phải là một số hữu tỉ"

c) Mệnh đề π < 3, 15 đúng vì π = 3,141592654…

 Mệnh đề phủ định: "π ≥ 3, 15"

d) Mệnh đề ‘’|–125| ≤ 0’’ sai vì |–125| = 125 > 0

 Mệnh đề phủ định: "|–125| > 0"