ÔN TẬP TOÁN HÌNH HỌC LỚP 8 HKI

Trang chủ » Chứng Minh Tứ Giác Bhck Là Hình Thoi » ÔN TẬP TOÁN HÌNH HỌC LỚP 8 HKI

Có thể bạn quan tâm

Gia sư toán - lý - hóa tp Hồ Chí Minh

Đào tạo + Gia sư TOÁN - Lý - HÓA tp Hồ Chí Minh

Thứ Bảy, 29 tháng 9, 2012

ÔN TẬP TOÁN HÌNH HỌC LỚP 8 HKI

ÔN TẬP TOÁN HÌNH HỌC LỚP 8 HKI

BÀI 1 : Cho tam giác ABC cân tại A.Gọi D, E, F theo thứ tự là trung điểm của AB, BC, AC. Vẽ điểm M là điểm đối xứng của điểm B qua điểm F và điểm N là điểm đối xứng của điểm E qua điểm D.1) Chứng minh: a/ Tứ giác BCFD là hình thang cân. b/ Tứ giác ADEF là hình thoi. c/ Tứ giác ABCM là hình bình hành. d/ Tứ giác ANBE là hình chữ nhật.

GIẢI.

a/ Tứ giác BCFD là hình thang cân. Xét 𝛥ABC, ta có : DA = DB (gt) FA = FC (gt) => DF là đường trung bình trong 𝛥ABC. => DF // BC => Tứ giác BCFD là hình thang Mà :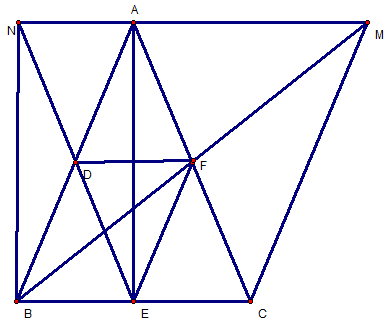 \widehat{ABC} =\widehat{ACB} (𝛥ABC cân tại A) => hình thang BCFD là hình thang cân. b / Tứ giác ADEF là hình thoi : Ta có : AB = AC (gt) AD = AB : 2 (gt) AF = AC : 2 (gt) => AD = AF = AC : 2 = AB : 2 (1) Xét ΔABC, ta có : DA = DB (gt) EB = EC (gt) => DE là đường trung bình => DE = AC : 2 (2) Cmtt, ta được : EF = BA : 2 (3) Từ (1), (2) và (3) ta được : AD = AF = DE = EF Vậy tứ giác ADEF là hình thoi. c/ Tứ giác ABCM là hình bình hành : Xét Tứ giác ABCM, ta có : FB = FM (M là điểm đối xứng của điểm B qua điểm F) FA = FC (gt) Mà hai đường chéo BM và AC cắt nhau tại F. =>Tứ giác ABCM là hình bình hành. d/ Tứ giác ANBE là hình chữ nhật : Xét ΔABC cân tại A, ta có : EB = EC (gt) =>AE là đường trung tuyến trong tam giác cân cũng là đường cao. => AE \bot BC hay \widehat{AEB} =90^0 Xét Tứ giác ANBE, ta có : Xét Tứ giác ABCM, ta có : DE = DN (N là điểm đối xứng của điểm E qua điểm D) DA = DB (gt) Mà hai đường chéo EN và AB cắt nhau tại D. =>Tứ giác ANBE là hình bình hành. Mà : \widehat{AEB} =90^0 (cmt) Nên : hình bình hành ANBE là hình chữ nhật. ———————————————————————————————— BÀI 2 : Cho hình thang cân ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. a/ Chứng minh: Tứ giác MNPQ làhình bình hành. b/ Chứng minh: Tứ giác MNPQ làhình thoi. c/ Nếu AC \bot BD thì tứ giác MNPQ là hình gì? Vì sao?

Giải

Tứ giác MNPQ làhình bình hành : Xét ABD, ta có : MA = MB (gt) QA = QD (gt) => MQ là đường trung bình. => MQ // BD và MQ = BD : 2 (1) Cmtt, ta được : NP // BD và NP = BD : 2 (2) NM // AC và NM = AC : 2 (3) Từ (1) và (2) : MQ // NP và MQ = PP => Tứ giác MNPQ làhình bình hành. b/Tứ giác MNPQ làhình thoi. ta có : AC = BD ( hai đường chéo hình thang cân ABCD) NM = AC : 2 (cmt) MQ = BD : 2 (cmt) => NM = MQ Xét hình bình hành MNPQ, ta có : NM = MQ (cmt) => hình bình hành MNPQ là hình thoi. c/Nếu AC \bot BD thì tứ giác MNPQ là hình gì? Nếu AC \bot BD NM // AC (cmt) NP // BD (cmt) => NM \bot NP tại N Hay \widehat{MNP} =90^0 Xét hình thoi MNPQ , ta có : \widehat{MNP} =90^0 (cmt) => hình thoi MNPQ là hình vuông. ——————————————————————————————————– BÀI 3 : Cho tam giác ABC vuông tại A (AB > AC), đường trung tuyến AO. Trên tia đối của tia OA lấy điểm D sao cho OD = OA.
  1. Chứng minh : ABDC là hình chữ nhật.
  2. Từ B kẻ BH vuông góc AD tại H, Từ C kẻ CK vuông góc AD tại K. chứng minh BH = CK và BK // CH.
  3. Tia BH cắt CD ở M, tia CK cắt AB ở K. chứng minh ba điểm M, O, N thẳng hàng.
  4. Trên tia đối của tia BH lấy điểm E sao cho BE = AD. Chứng minh \widehat{DCE}=45^0

GIẢI.

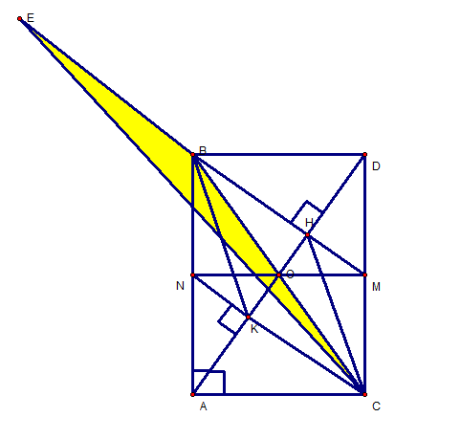1. ABDC là hình chữ nhật : Xét tứ giác ABDC, ta có : OB = OC (đường trung tuyến AO của ABC) OA = OD (gt) => tứ giác ABDC là hình bình hành Mà : \widehat{}=90^0 (gt) => hình bình hành ABDC là hình chữ nhật 2. BH = CK và BK // CH : Xét 𝛥HOB và 𝛥OC, ta có : \widehat{BHO}=\widehat{CKO}=90^0 (gt) OB = OC (cmt) \widehat{O_1}=\widehat{O_2} (đối đỉnh) => 𝛥HOB = 𝛥OC => OH = OK (cạnh tương ứng) Xét tứ giác BHCK, ta có : OH = OK (cmt) OB = OC (cmt) Mà hai đường chéo BC và HK cắt nhau tại O => tứ giác BHCK là hình bình hành => BH = CK và BK // CH 3. chứng minh ba điểm M, O, N thẳng hàng. Xét tứ giác BMCN, ta có : BM // CN (cùng vuông góc AD) BN // CM => tứ giác BMCN là hình bình hành => hai đường chéo BC và NM cắt nhau tại trung điểm mỗi đường Mà : OB = OC (cmt) => OM = ON Hay N, O, M thẳng hàng. 4. Chứng minh \widehat{DCE}=45^0 Ta có : BC = AD (hai đường chéo của hình chữ nhật ABDC ) BE = AD (gt) => BE = BC => tam giác EBC cân tại B => \widehat{BCE}=\widehat{BEC} Mà : \widehat{ECN}=\widehat{BEC} (so le trong) => \widehat{ECN}=\widehat{BCE} (1) Mặt khác : OD = OC (O là giao điểm hai đường chéo hình chữ nhật) => tam giác COD cân tại O => \widehat{DCB}=\widehat{ADC} Mà : \widehat{ADC}=\widehat{NCA} (cùng phụ với góc DAC) => \widehat{ NCA }=\widehat{DCB} (2) Cộng (1) và (2), ta được : \widehat{ NCA }+\widehat{ECN}=\widehat{DCB}+\widehat{BCE} => \widehat{ECA}=\widehat{DCE} => CE là tia phân giác góc ACD => \widehat{DCE}=\widehat{ACD} : 2= 45^0

======================================================================

BÀI TẬP RÈN LUYỆN :

BÀI 1 : Cho tam giác ABC vuông ở C . Gọi M , N lần lượt là trung điểm của BC , AB . Gọi P là điểm đối xứng của M qua N . a / Chứng minh :Tứ giác MBPA là hình bình hành. b / Chứng minh : Tứ giác PACM là hình chữ nhật . c / CN cắt PB ở Q . Chứng minh BQ = 2 PQ d / Tam giác ABC có thêm điều kiện gì thì hình chữ nhật PACM là hình vuông . BÀI 2 : Cho hình bình hành ABCD có M là trung điểm AB và N là trung điểm CD. a/ Chứng minh : tứ giác AMND là hình bình hành. b/ Chứng minh : tứ giác AMCN là hình bình hành. c/ Chứng minh : AC, BD, MN đồng quy. d/ Hình bình hành ABCD có điều kiện gì thì tứ giác AMND là hình chữ nhật, hình thoi, hình vuông. BÀI 3 : Cho tam giác ABC. Gọi D, E lần lượt là trung điểm của AB và BC. a.Chứng minh tứ giác ADEC là hình thang b.Trên tia đối của tia DE lấy điểm F sao cho DF = DE.Chứng minh tứ giác AEBF là hình bình hành. c.Với điều kiện nào của tam giác ABC để AEBF là hình vuông?. BÀI 4 : Cho hình thang cân ABCD (AB // CD). Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA.Biết AC vuông góc BD a/ Chứng minh: Tứ giác MNPQ làhình bình hành. b/ Chứng minh: Tứ giác MNPQ làhình thoi. c/ Nếu AC vuông góc BD thì tứ giác MNPQ là hình gì? Vì sao? BÀI 5 : Cho DABC vuông tại A, vẽ trung tuyến AM.
  1. Nếu cho AB = 6cm, AC = 8cm. Tính độ dài đoạn thẳng AM.
  2. Gọi D, E lần lượt là trung điểm của AB, AC. Chứng minh tứ giác AEMD.
  3. Gọi F là điểm đối xứng của điểm E qua D. Tứ giác EFBC làhình gì? Chứng minh.
  4. DABC cần có thêm điều điện gì thì AEMDlà hình vuông?
Người đăng: Unknown vào lúc 01:19 Nhãn: Hình Học 8, Tứ giác

Không có nhận xét nào:

Đăng nhận xét

Bài đăng Mới hơn Bài đăng Cũ hơn Trang chủ Đăng ký: Đăng Nhận xét (Atom)

Tìm kiếm Blog này

Chương trình toán phổ thông :

  • Hình Học 10 (8)
  • Hình Học 11 (1)
  • Hình Học 12 (1)
  • Hình Học 6 (1)
  • Hình Học 7 (8)
  • Hình Học 8 (9)
  • Hình Học 9 (9)
  • Đại Số 10 (5)
  • Đại Số 7 (9)
  • Đại Số 8 (9)
  • Đại Số 9 (7)
  • Đề thi TS lớp 6 Trần Đại Nghĩa (3)

Nhập công thức toán học

Bước 1 : Nhập công thức. Launch CodeCogs Equation Editor

Bước 2 : Copy đoạn code, sau đó paste vào phẩn hồi

Tổng số lượt xem

Từ khóa » Chứng Minh Tứ Giác Bhck Là Hình Thoi