Phát Biểu định Lí Ta – Lét Trong Không Gian.

Trang chủ » định Lí Ta Lét Trong Không Gian » Phát Biểu định Lí Ta – Lét Trong Không Gian.

Có thể bạn quan tâm

Đăng nhập Facebook GOOGLE Google IMG

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 11 Toán

Câu hỏi:

23/07/2024 531

Phát biểu định lí Ta – lét trong không gian.

Xem lời giải Câu hỏi trong đề: Giải SGK Toán 11 Hình học - Chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song Bắt Đầu Thi Thử

Trả lời:

verified Giải bởi Vietjack

Định lí Ta – lét trong không gian:

- Định lí thuận (Định lí Ta – lét)

Ba mặt phẳng đôi một song song chắn trên hai cát tuyến bất kì các đoạn thẳng tương ứng tỉ lệ, nghĩa là:

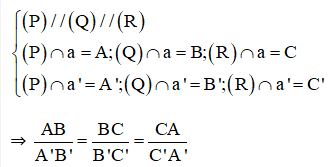
Phát biểu định lí Ta – lét trong không gian. Định lí Ta – lét trong không gian (ảnh 1)

- Định lí đảo (Định lí Ta – lét đảo)

Giả sử trên hai đường thẳng a và a' lần lượt lấy hai bộ ba điểm (A, B, C) và (A', B', C') sao cho AB/A'B'= BC/B'C' = CA/C'A'

Khi đó ba đường thẳng AA', BB', CC' cùng song song với một mặt phẳng, nghĩa là ba đường thẳng đó nằm trên ba mặt phẳng song song với nhau.

Câu trả lời này có hữu ích không?

0 1

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Nêu phương pháp chứng minh.

- Đường thẳng song song với đường thẳng;

- Đường thẳng song song với mặt phẳng;

- Mặt phẳng song song với mặt phẳng.

Xem đáp án » 07/12/2021 4,311

Câu 2:

Nêu cách xác định thiết diện được tạo bởi một mặt phẳng với một hình chóp, hình hộp, hình lăng trụ.

Xem đáp án » 07/12/2021 413

Câu 3:

Hãy nêu các cách xác định mặt phẳng, kí hiệu mặt phẳng.

Xem đáp án » 07/12/2021 314

Câu 4:

Thế nào là đường thẳng song song với đường thẳng, đường thẳng song song với mặt phẳng, mặt phẳng song song với mặt phẳng.

Xem đáp án » 07/12/2021 236

Câu 5:

Nêu phương pháp chứng minh ba đường thẳng đồng quy.

Xem đáp án » 07/12/2021 228

Câu 6:

Nêu phương pháp chứng minh ba điểm thẳng hàng.

Xem đáp án » 07/12/2021 226 Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »
  • Trắc nghiệm tổng hơp Toán 11 (có đáp án) 76 đề 24154 lượt thi Thi thử
  • Trắc nghiệm Đề thi Toán 11 (có đáp án) 17 đề 8612 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án) 12 đề 5091 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 4: Giới hạn (có đáp án) 7 đề 4389 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (có đáp án) 8 đề 4104 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án) 11 đề 3930 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Ôn tập chương 2: Tổ hợp - Xác suất (có đáp án) 15 đề 3367 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác (có đáp án) 6 đề 3295 lượt thi Thi thử
  • Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản (có đáp án) 6 đề 3210 lượt thi Thi thử
  • Trắc nghiệm Biến cố và xác suất của biến cố có đáp án 4 đề 3121 lượt thi Thi thử
Xem thêm » Hỏi bài

Câu hỏi mới nhất

Xem thêm »

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?

    Một vòng quay trò chơi có bán kính 57 m Khi quay một vòng lần thứ nhất tính từ (ảnh 1) 280 18/04/2024 Xem đáp án

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?

    Một vòng quay trò chơi có bán kính 57 m Khi t = 0 (phút) thì khoảng cách từ cabin (ảnh 1) 152 18/04/2024 Xem đáp án

  • Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

    \(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

    với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

    Tính chu kì của hàm số h(t)?

    Một vòng quay trò chơi có bán kính 57 m Tính chu kì của hàm số h(t) (ảnh 1) 133 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = sin x, tìm:

    Các khoảng giá trị của x để hàm số y = sin x nhận giá trị dương. 140 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = sin x, tìm:

    Các giá trị của x để sin x = \(\frac{1}{2}\);

    134 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = cos x, cho biết:

    Có bao nhiêu giá trị của x trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\) để cos x = 0.

    127 18/04/2024 Xem đáp án

  • Từ đồ thị hàm số y = cos x, cho biết:

    Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;

    132 18/04/2024 Xem đáp án

  • Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

    y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).

    132 18/04/2024 Xem đáp án

  • Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

    y = sin x trên khoảng \(\left( { - \frac{{19\pi }}{2};\, - \frac{{17\pi }}{2}} \right),\,\,\left( { - \frac{{13\pi }}{2};\, - \frac{{11\pi }}{2}} \right)\);

    134 18/04/2024 Xem đáp án

  • Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

    \(y = \frac{1}{{4 - \sin x}}\).

    142 18/04/2024 Xem đáp án
Xem thêm »

Từ khóa » định Lí Ta Lét Trong Không Gian