Phương Pháp đặt Nhân Tử Chung Và Bài Tập Vận Dụng - Toán Lớp 8

Bài viết dưới đây sẽ giúp các em hiểu rõ về phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử là như thế nào? Tại sao cần phân tích đa thức thành nhân tử?

I. Lý thuyết phân tích đa thức thành nhân tử bằng cách đặt nhân tử chung.

• Phân tích đa thức thành nhân tử là làm gì?

- Khái niệm: Phân tích đa thức thành nhân tử (hay thừa số) là biến đổi đa thức đó thành một tích của những đa thức.

• Ứng dụng của việc phân tích đa thức thành nhân tử

- Việc phân tích đa thức thành nhân tử giúp chúng ta rút gọn được biểu thức, tính nhanh, giải phương trình.

• Phương pháp đặt nhân tử chung để phân tích đa thức thành nhân tử

- Bằng cách phân tích (tách, ghép,... các hạng tử) để khi tất cả các số hạng của đa thức có một thừa số chung, ta đặt thừa số chung đó ra ngoài dấu ngoặc () để làm nhân tử chung.

- Các số hạng bên trong dấu () có được bằng cách lấy số hạng của đa thức chia cho nhân tử chung.

> Lưu ý: Nhiều khi để làm xuất hiện nhân tử chung ta cần đổi dấu các hạng tử bằng cách vận dụng tính chất A = -(-A).

II. Bài tập vận dụng phương pháp đặt nhân tử chung

* Bài 39 trang 19 SGK Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

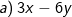
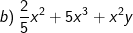
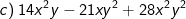
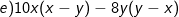
* Lời giải Bài 39 trang 19 SGK Toán 8 Tập 1:

a) 3x – 6y = 3.x – 3.2y

 (xuất hiện nhân tử chung là 3)

 = 3(x – 2y).

 

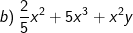
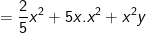
 (xuất hiện nhân tử chung x2)

 

 

 

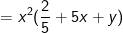
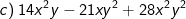
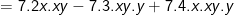
 (xuất hiện nhân tử chung 7xy)

 

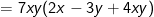
 (có nhân tủ chung là (2/5)(y-1))

 

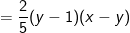
e) 10x(x – y) – 8y(y – x)

 (Vì x – y = –(y – x) nên ta đổi y – x về x – y)

 = 10x(x – y) – 8y[–(x – y)]

 = 10x(x – y) + 8y(x – y)

 = 2(x – y).5x + 2(x – y).4y

 (xuất hiện nhân tử chung 2(x – y))

 = 2(x – y)(5x + 4y)

* Bài 40 trang 19 SGK Toán 8 Tập 1: Tính giá trị của biểu thức:

a) 15.91,5 + 150.0,85

b) x(x – 1) – y(1 – x) tại x = 2001 và y = 1999

* Lời giải Bài 40 trang 19 SGK Toán 8 Tập 1: 

a) 15.91,5 + 150.0,85  = 15.91,5 + 15.10.0,85

 = 15.91,5 + 15.8,5  = 15(91,5 + 8,5)

 = 15.100 = 1500

b) x(x – 1) – y(1 – x) = x(x – 1) – y[–(x – 1)]

 = x(x – 1) + y(x – 1) = (x – 1)(x + y)

 Tại x = 2001, y = 1999, giá trị biểu thức bằng:

 (2001 – 1)(2001 + 1999) = 2000.4000 = 8000000

* Bài 41 trang 19 SGK Toán 8 Tập 1: Tìm x, biết:

a) 5x(x – 2000) – x + 2000 = 0

b) x3 – 13x = 0

* Lời giải Bài 41 trang 19 SGK Toán 8 Tập 1: 

a) 5x(x – 2000) – x + 2000 = 0

 ⇔ 5x(x – 2000) – (x – 2000) = 0

 (Có nhân tử chung là x - 2000)

 ⇔ (x – 2000).(5x – 1) = 0

 ⇔ x – 2000 = 0 hoặc 5x – 1 = 0

+TH1: x – 2000 = 0 ⇔ x = 2000

+TH2: 5x – 1 = 0 ⇔ 5x = 1 ⇔ x = 1/5.

 → Vậy có hai giá trị của x thỏa mãn là x = 2000 và x = 1/5.

b) x3 = 13x ⇔ x3 – 13x = 0

 ⇔ x.x2 – x.13 = 0. (Có nhân tử chung x)

 ⇔ x(x2 – 13) = 0

 ⇔ x = 0 hoặc x2 – 13 = 0

 Với  x2 – 13 = 0 ⇔ x2 = 13 ⇔ x = √13 hoặc x = –√13

→ Vậy có 3 giá trị của x thỏa mãn là: x = 0, x = √13 và x = –√13.

* Bài 42 trang 19 SGK Toán 8 Tập 1: Chứng minh rằng 55n + 1 – 55n chia hết cho 54 (với n là số tự nhiên).

* Lời giải Bài 42 trang 19 SGK Toán 8 Tập 1: 

- Ta có : 55n + 1 – 55n = 55n.55 – 55n

 = 55n(55 – 1) = 55n.54

- Vì 54 chia hết cho 54 nên 55n.54 luôn chia hết cho 54 với mọi số tự nhiên n.

→ Vậy 55n + 1 – 55n chia hết cho 54.