Phương Trình Tách Biến, Phương Trình đẳng Cấp Cấp 1
Có thể bạn quan tâm
Maths 4 Physics & more…
Blog Toán Cao Cấp (M4Ps)Tìm
Search for: Đi- Author
- Bài viết
- Bài giảng
- Giải tích 1
- Hàm số – Hàm lượng giác ngược – Hàm hyperbol
- Chia một đa thức cho tam thức bậc 2
- Giới hạn của hàm số (Limit of a function)
- Vô cùng bé (infinitesimal)
- Đạo hàm và vi phân của hàm số (derivative and differential of a function)
- Khai triển Taylor – Maclaurin (Taylor expansion)
- Khảo sát đường cong tham số
- Tích phân hữu tỷ (integration by partial fractions)
- Tích phân hàm vô tỉ (Integrals involving roots)
- Tích phân suy rộng (Improper Integrals)
- Chuỗi số. Tổng của chuỗi (Series. The total sum of series)
- Chuỗi số dương (Infinitive Series)
- Chuỗi Fourier
- Chuỗi Fourier Sine và Cosine
- Giải tích 2
- Khái niệm mở đầu về hàm nhiều biến
- Giới hạn của hàm hai biến số
- Đạo hàm riêng
- Hàm số khả vi và vi phân toàn phần
- Đạo hàm của hàm hợp
- Đạo hàm hàm số ẩn
- Cực trị (không điều kiện) của hàm 2 biến
- Cực trị có điều kiện (cực trị ràng buộc)
- Các khái niệm cơ bản của phương trình vi phân
- Phương trình tách biến, phương trình đẳng cấp cấp 1
- Phương trình vi phân tuyến tính cấp 1, Bernoulli, Ricatti
- Phương trình vi phân tuyến tính cấp 2 (linear second-order ordinary differential equation)
- Ứng dụng chuỗi số giải phương trình vi phân
- Tích phân hai lớp (Tích phân kép)
- Tích phân hai lớp trong tọa độ cực. Công thức đổi biến
- Tích phân đường theo tọa độ (Tp đường loại 2)
- Số phức (Complex Number)
- Đại số tuyến tính (Linear Algebra)
- Tập hợp
- Khái niệm về ma trận
- Ma trận bậc thang (Echelon matrix)
- Ma trận nghịch đảo (khả nghịch)
- Thuật toán tìm ma trận bậc thang
- Định thức (Determinants)
- Hệ phương trình tuyến tính (System of Linear Equations)
- Khái niệm về ánh xạ tuyến tính
- Không gian vectơ Euclide (Euclidean Vector Spaces)
- Trị riêng, vectơ riêng của ma trận (Eigenvalues and Eigenvectors)
- Dạng toàn phương
- Xác suất thống kê
- Bổ túc về Giải tích Tổ hợp
- Biến cố và quan hệ giữa các biến cố
- Các định nghĩa của xác suất
- Xác suất có điều kiện
- Đại lượng ngẫu nhiên 1 chiều
- Một số quy luật phân phối xác suất rời rạc
- Ước lượng tham số của tổng thể
- Kiểm định giả thiết
- Phương pháp Toán Lý (PT Đạo hàm riêng và PBĐ Laplace)
- Phép biến đổi Laplace – Các khái niệm mở đầu
- Giải tích 1
- Bài tập
- Trắc nghiệm
- Thảo luận
- Thảo luận (tiếp theo)
- Thảo luận chung (tt)
- Thảo luận về giải tích
- Thảo luận Giải tích – Trang 2
- Thảo luận ĐSTT
- Trang 2
- Trang 3
- Thảo luận XSTK
- Trang 2
- Thảo luận về tích phân bội
- Đề thi
- Ebooks
- Maths Ebooks
- Giải tích – Đại số
- XSTK – Phương pháp tính
- Hàm phức – PDEs
- Tài liệu khác
- Giáo dục – Khoa học
- Thư giãn
- Maths Ebooks
- Một thời để nhớ
- Softwares
- Links
- Sitemap
Shortlink: http://wp.me/P8gtr-MB
Phương trình cấp một tổng quát có dạng F(x,y,y’) = 0 (I)
Nếu giải ra được đối với y’ thì phương trình có thể viết dưới dạng:
hoặc:
hoặc:
Chú ý quan trọng:
– Thông thường, ta nên tìm cách biến đổi phương trình về dạng (1) và phân tích f(x,y) ở vế phải để biết dạng. Đa số, các phương trình đều có thể đưa được về 1 trong 6 dạng sau: phân ly biến số, đẳng cấp (thuần nhất), phương trình đưa về pt đẳng cấp được, pt tuyến tính, pt Bernoulli và pt vi phân toàn phần.
– Nếu từ (1) ta không đưa pt về 1 trong 6 dạng trên được thì thử nghịch đảo phương trình (2) đưa phương trình về dạng x là hàm số theo biến y. Nghĩa là: thì sẽ tìm được cách giải.
1. Bài toán cauchy (Bài toán điều kiện đầu):
Bài toán Cauchy là bài toán tìm nghiệm ptvp:
thỏa mãn điều kiện đầu:
Nghĩa là: tìm đường cong y = y(x) đi qua điểm (x0;y0) và thỏa mãn pt (1)
2. Định lý Peano – Cauchy – Picard (định lý tồn tại và duy nhất nghiệm):
Nếu hàm số f(x,y) liên tục trong miền mở
, thì với mọi điểm
, bài toán Cauchy (1), (2) có nghiệm xác định trong 1 lân cận của x0.
Ngoài ra, nếu đạo hàm riêng
cũng liên tục trong D thì nghiệm đó là duy nhất.
(ta công nhận định lý này, vì việc chứng minh vượt quá những kiến thức chúng ta được trang bị)
3. Nghiệm tổng quát:
Nghiệm tổng quát của pt (1) là hàm số , phụ thuộc biến x, và hằng số C, và thỏa mãn các điều kiện:
1. Nghiệm đúng ptvp với mọi giá trị cụ thể của C.
2. Với bất kỳ điều kiện đầu ta cũng có thể tìm được
sao cho hàm số
thỏa mãn điều kiện đầu
– Trong quá trình tìm nghiệm: nếu ta đi đến biểu thức (*) mà không giải được đối với y thì y là hàm ẩn theo x, C xác định bởi pt (*) và (*) được gọi là tích phân tổng quát.
– Các nghiệm của phương trình không suy ra được từ nghiệm tổng quát được gọi là nghiệm kỳ dị.
4. Phương trình phân ly biến số (tách biến)
Là phương trình có dạng:
(hoặc
)
Nghĩa là: ở vế phải ta gom được x đứng riêng và y đứng riêng (hoặc M(x) chỉ là hàm theo 1 biến số x và N(y) chỉ là hàm theo 1 biến số y)
4.1 Cách giải:
Ta biến đổi như sau:
Bằng cách lấy tích phân (vế trái theo y, vế phải theo x) ta được nghiệm tổng quát:
4.2 Ví dụ:
1. Giải phương trình:
Chuyển phương trình về dạng (1) ta có:
Vậy: x tách riêng, và y tách riêng nên đây là phương trình tách biến.
Khi đó ta có:
Ở đây do 2 vế đều có chứa ln nên thay vì ta chọn hằng số C thì ta chọn hằng số là lnC để dễ dàng rút gọn
Vậy nghiệm phương trình:
Hay:
2. Giải phương trình
Ta có: (phương trình tách biến)
Do đó:
Suy ra:
Bài này, ta cần xét thêm trường hợp tgy = 0.
3. Ví dụ tự giải:
4.3 Nhận xét:
Phương trình dạng
có thể đưa về phương trình tách biến bằng cách đổi qua ẩn hàm mới
Thật vậy, ta có:
Vậy vế phải là biểu thức chỉ phụ thuộc z. Nghĩa là z tách riêng và x tách riêng nên nó là phương trình tách biến.
5. Phương trình đẳng cấp:
– Hàm F(x,y) được gọi là hàm đẳng cấp bậc k nếu:
với mọi λ > 0, ta có:
– Ví dụ: Các hàm lần lượt là các hàm đẳng cấp bậc 0, bậc 1, bậc 3. Hàm
không là hàm đẳng cấp
5.1 Phương trình vi phân đẳng cấp: Phương trình được gọi là phương trình đẳng cấp nếu: f(x,y) là hàm đẳng cấp bậc 0, nghĩa là
– Lưu ý: một số giáo trình gọi tên dạng phương trình này là phương trình thuần nhất
– Nhận xét: Giả sử thì để (1) là phương trình đẳng cấp thì tất cả mọi số hạng có trong M(x,y) và N(x,y) phải cùng bậc.
– Ví dụ: phương trình: là phương trình đẳng cấp vì các số hạng đều là bậc 2. Phương trình:
là phương trình đẳng cấp vì
đều là các số hạng bậc 1.
5.2 Cách giải:
Theo định nghĩa pt đẳng cấp ta có: . Chọn
thì pt (1) có dạng:
(*)
Vế phải của pt (*) là 1 biểu thức luôn phụ thuộc y/x . Do vậy:
Đặt
Thế vào phương trình (5) ta có:
– Th1: Nếu
Khi đó:
Do đó pt (5) trở thành:
– Th2: Nếu
Khi đó: : pt tách biến.
5.3 Ví dụ: Giải phương trình vi phân:
Rõ ràng đây là phương trình đẳng cấp. Ta viết lại phương trình như sau:
Đặt: . Ta có:
, và thay vào phương trình ta có:
Lấy tích phân 2 vế ta được:
Hay:
Vậy nghiệm của phương trình có dạng:
Đánh giá:
Chia sẻ:
- In
Trang: 1 2
Thảo luận
31 bình luận về “Phương trình tách biến, phương trình đẳng cấp cấp 1”
Bình luận về bài viết này Hủy trả lời
Translators & RSS
![]()
![]()
![]()

Đăng ký nhận tin
Bạn hãy nhập địa chỉ email của mình để đăng ký theo dõi tin tức từ blog này và nhận những bài viết mới nhất qua địa chỉ email.
Địa chỉ email:
Sign me up!
Tham gia cùng 2 793 người đăng ký khácĐôi lời
Bạn có thể theo dõi các lời bình liên quan đến lời bình của mình qua email bằng cách chọn dòng thông báo Báo cho bạn khi có người bình luận tiếp theo đề tài này bằng điện thư mỗi khi viết 1 lời bình.
Rất mong các bạn viết lời nhắn bằng tiếng việt có dấu nhé.
Để viết tiếng việt có dấu bạn dùng font chữ Unicode và bảng mã là Unicode UTF-8.
Để biết cách gõ công thức Toán học trong các lời nhắn ở trang web này, mời bạn đọc bài hướng dẫn tại đây hoặc bạn có thể xem bài hướng dẫn dùng MathType tại đây và bài tạo công thức trực tuyến tại đây

Lời nhắn mới nhất
| Dương Khánh Uyên trong Trang 2 | |
| Trần Thái An trong Trang 2 | |
| Chúc Chúc trong Xác suất có điều kiện | |
| Hoang Anh trong Khai triển Taylor – Macl… | |
| Trần Trung Đức trong Mẹo phân tích nhanh 1 phân… | |
| Nhung Duong trong Trang 2 | |
| khoi trong Khai triển Taylor – Macl… | |
| Minh pham trong Chuỗi Fourier Sine và Cos… | |
| Minh Phạm trong Chuỗi Fourier | |
| Anh Tuấn trong Cực trị (không điều kiện) của… |
Bài “hot”
- Khai triển Taylor - Maclaurin (Taylor expansion)
- Phương trình vi phân tuyến tính cấp 1, Bernoulli, Ricatti
- Ma trận nghịch đảo (khả nghịch)
- Cực trị (không điều kiện) của hàm 2 biến
- Phương trình tách biến, phương trình đẳng cấp cấp 1
- Tích phân đường theo tọa độ (Tp đường loại 2)
- Tích phân hai lớp (Tích phân kép)
- Phương trình vi phân tuyến tính cấp 2 (linear second-order ordinary differential equation)
- Đạo hàm riêng
- Dạng toàn phương
Bài viết chuyên đề
- Bài giảng (20)
- Video bài giảng (4)
- Bài viết (192)
- Bài viết về ICT (59)
- Cảnh báo virus (1)
- giaovien.net (6)
- Mẹo Wordpress (13)
- Thủ thuật Gmail (7)
- Giáo dục (29)
- Khoa học (51)
- Thư giãn (45)
- Bài viết về ICT (59)
- Bí quyết học tập (20)
- Cuộc sống sinh viên (26)
- Hình ảnh và Tin tức (32)
- Làm theo lời Bác (9)
- Life's Art (61)
- nguyên tắc sáng tạo (27)
- Toán học (104)
- Lịch sử Toán học (13)
- Liên kết Toán học (6)
- Luyện thi Đại học (7)
- Đề thi thử (4)
- Vẻ đẹp Toán học (8)
- Đố vui (36)
Maths 4 Physics & more…
Blog tại WordPress.com.
Trang này sử dụng cookie. Tìm hiểu cách kiểm soát ở trong: Chính Sách Cookie- Theo dõi Đã theo dõi
-
 Maths 4 Physics & more... Đã có 938 người theo dõi Theo dõi ngay
Maths 4 Physics & more... Đã có 938 người theo dõi Theo dõi ngay - Đã có tài khoản WordPress.com? Đăng nhập.
-
-
-
 Maths 4 Physics & more...
Maths 4 Physics & more... - Theo dõi Đã theo dõi
- Đăng ký
- Đăng nhập
- URL rút gọn
- Báo cáo nội dung
- Xem toàn bộ bài viết
- Quản lý theo dõi
- Ẩn menu
-
Từ khóa » Giải Phương Trình Dx Dy
-
Toán - Hướng Dẫn Giải Bt Phương Trình Vi Phân Thường
-
[PDF] BÀI 5: PHƯƠNG TRÌNH VI PHÂN - Topica
-
Hướng Dẫn Giải Bt Phương Trình Vi Phân Thường_CBM_Uneti 2009 ...
-
[PDF] PHƯƠNG TRÌNH VI PHÂN
-
Giải Tích 2 - Chương 4 - Bài 1: Phương Trình Vi Phân Cấp 1 P1
-
Giải Và Biện Luận Hệ Hai Phương Trình Bậc Nhất Hai ẩn Có Chứa Tham ...
-
Phương Trình Vi Phân Tuyến Tính Cấp 1, Bernoulli, Ricatti
-
Tìm Dy/dx (dy)/(dx)=xy | Mathway
-
Chương 4 Phương Trình Vi Phân - Tài Liệu Text - 123doc
-
Chương 5: Phương Trình Vi Phân - 123doc
-
Giáo án Đại Số 10 NC Tiết 36: Hệ Phương Trình Bậc Nhất Nhiều ẩn (tiếp)
-
Bài Giảng Toán Cao Cấp - Chương 8. Phương Trình Vi Phân
-
Giải Phương Trình Vi Phân $(x-y+4)dy+(x+y-2)dx=0$ - Giải Tích
Ad giúp e bài này với.xy’=y-xe^y/x tks trc ạ.
ThíchThích
Được đăng bởi Huy | 12/10/2016, 21:24 Reply to this commentThay oi giai bai nay jum em 2ydx+(y^2-6x)dy=0
ThíchThích
Được đăng bởi ctkt chau | 23/06/2015, 22:21 Reply to this commentthầy ơi giải giúp em bài này xiu hen: giải pt: xsqrt(y^2+2xy+2x^2)dy =(2xy+3x^2)dy-(2y^2+3xy)dx điều kiện: y*(1+sqrt(2))=0 e cảm ơn thầy
ThíchThích
Được đăng bởi nguyễn thành hậu | 21/01/2015, 10:09 Reply to this commentthầy ơi giải giúp em bài này với ah (y+e^x)dx+xdy=0
ThíchThích
Được đăng bởi sue | 12/01/2015, 11:46 Reply to this commentthầy oi giup dùm e :phuong trinh tach biến :y’=x^2*y^2
ThíchThích
Được đăng bởi duyen doanthikim | 10/01/2015, 08:11 Reply to this commentthầy ơi giúp em bai nay ạ: xy’-2y=2. x^3
ThíchThích
Được đăng bởi Lục Bình | 15/07/2014, 09:56 Reply to this commentthầy ơi sao thầy không lấy thêm nhiều bài tập ví dụ nữa thầy? em thấy bài tập nó hơi ít ah!
ThíchThích
Được đăng bởi thanh lam | 26/11/2012, 20:40 Reply to this commentbên trên khi đặt x=u+h e nghĩ bên dưới la y=v+k chứ thầy
ThíchThích
Được đăng bởi Đỗ Khánh Duy | 10/06/2011, 03:06 Reply to this commentem thắc mắc tại sao ở vd 5.3 thầy không xét TH x=0 với x#0 ?????? Thầy có thể giải thích rõ tại sao không xét không
ThíchThích
Được đăng bởi Tuan Vu | 31/01/2011, 19:51 Reply to this commentthầy cho em hỏi bài giải phương trình vi phân :y’=x+y .cám ơn thầy ^^
ThíchThích
Được đăng bởi Lam Như | 23/10/2010, 22:06 Reply to this commentThầy ơi, em bị bí bài này thầy giải giúp em với ạ: Xét PTVP (y^2-2xy)dx+(x^2-5xy)dy=0. Khẳng định nào sau đây dúng: 1.PTVP dẳng cấp 2. PTVP Bernoulli 3.PTVP tách biến 4.PTVI tuyến tính
ThíchThích
Được đăng bởi Mộng Tuyền | 18/09/2010, 09:45 Reply to this commentĐể tìm dạng ptvp, em cứ biến đổi về dạng: . Sau đó, phân tích f(x,y) để tìm ra dạng của nó. Ở đây, em có
. Sau đó, phân tích f(x,y) để tìm ra dạng của nó. Ở đây, em có  Tất cả số hạng ở vế phải đều có bậc là 2 nên
Tất cả số hạng ở vế phải đều có bậc là 2 nên 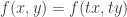 . Vậy nó là dạng pt gì chắc em đã nhận ra.
. Vậy nó là dạng pt gì chắc em đã nhận ra.
ThíchThích
Được đăng bởi 2Bo02B | 18/09/2010, 10:12 Reply to this comment