Thuật Toán Merge Sort – Sắp Xếp Trộn - Đào Tạo Tin Học Trực Tuyến

View: 152

Thuật toán sắp xếp merge sort là một trong những thuật toán có độ phức tạp ở mức trung bình và cùng sử dùng phương pháp chia để trị giống thuật toán sắp xếp nhanh quick sort. Thuật toán này không chỉ áp dụng trong sắp xếp mà còn ở nhiều bài toán khác.

NỘI DUNG

Toggle

• Ý tưởng của thuật toán merge sort
• Minh họa thuật toán sắp xếp Merge sort:

Ý tưởng của thuật toán merge sort

Giống như Quick sort, Merge sort là một thuật toán chia để trị. Thuật toán này chia mảng cần sắp xếp thành 2 nửa. Tiếp tục lặp lại việc này ở các nửa mảng đã chia. Sau cùng gộp các nửa đó thành mảng đã sắp xếp. Hàm merge() được sử dụng để gộp hai nửa mảng. Hàm merge(arr, l, m, r) là tiến trình quan trọng nhất sẽ gộp hai nửa mảng thành 1 mảng sắp xếp, các nửa mảng là arr[l…m] và arr[m+1…r] sau khi gộp sẽ thành một mảng duy nhất đã sắp xếp. Hãy xem ý tưởng triển khai code dưới đây để hiểu hơn:

mergeSort(arr[], l, r) If r > l 1. Tìm chỉ số nằm giữa mảng để chia mảng thành 2 nửa: middle m = (l+r)/2 2. Gọi đệ quy hàm mergeSort cho nửa đầu tiên: mergeSort(arr, l, m) 3. Gọi đệ quy hàm mergeSort cho nửa thứ hai: mergeSort(arr, m+1, r) 4. Gộp 2 nửa mảng đã sắp xếp ở (2) và (3): merge(arr, l, m, r)

Sơ đồ cụ thể của thuật toán Merge Sort:

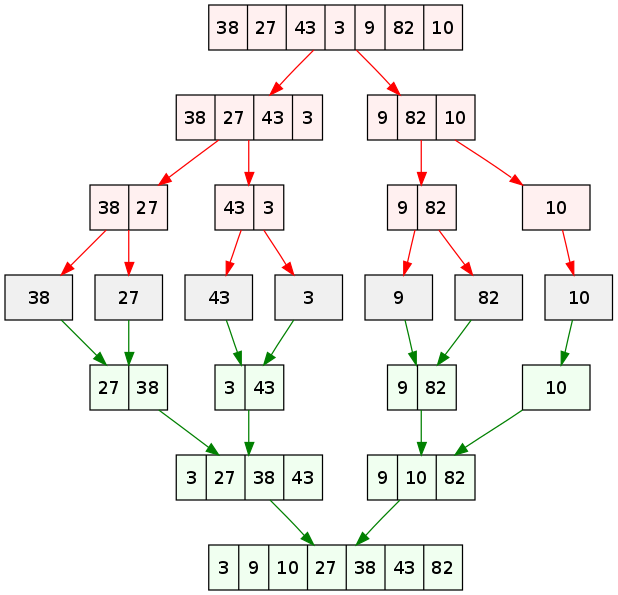
Minh họa thuật toán sắp xếp Merge sort:

#include <iostream> using namespace std; void merge(int array[], int const left, int const mid, int const right){ auto const subArrayOne = mid - left + 1; auto const subArrayTwo = right - mid; auto *leftArray = new int[subArrayOne], *rightArray = new int[subArrayTwo]; for (auto i = 0; i < subArrayOne; i++) leftArray[i] = array[left + i]; for (auto j = 0; j < subArrayTwo; j++) rightArray[j] = array[mid + 1 + j]; auto indexOfSubArrayOne = 0, indexOfSubArrayTwo = 0; int indexOfMergedArray = left; while (indexOfSubArrayOne < subArrayOne && indexOfSubArrayTwo < subArrayTwo) { if (leftArray[indexOfSubArrayOne] <= rightArray[indexOfSubArrayTwo]) { array[indexOfMergedArray] = leftArray[indexOfSubArrayOne]; indexOfSubArrayOne++; } else { array[indexOfMergedArray] = rightArray[indexOfSubArrayTwo]; indexOfSubArrayTwo++; } indexOfMergedArray++; } while (indexOfSubArrayOne < subArrayOne) { array[indexOfMergedArray] = leftArray[indexOfSubArrayOne]; indexOfSubArrayOne++; indexOfMergedArray++; } while (indexOfSubArrayTwo < subArrayTwo) { array[indexOfMergedArray] = rightArray[indexOfSubArrayTwo]; indexOfSubArrayTwo++; indexOfMergedArray++; } } void mergeSort(int array[], int const begin, int const end) { if (begin >= end) return; auto mid = begin + (end - begin) / 2; mergeSort(array, begin, mid); mergeSort(array, mid + 1, end); merge(array, begin, mid, end); } void printArray(int A[], int size) { for (auto i = 0; i < size; i++) cout << A[i] << " "; } int main() { int arr[] = { 12, 11, 13, 5, 6, 7 }; auto arr_size = sizeof(arr) / sizeof(arr[0]); cout << "Given array is \n"; printArray(arr, arr_size); mergeSort(arr, 0, arr_size - 1); cout << "\nSorted array is \n"; printArray(arr, arr_size); return 0; }