Thuật Toán Sắp Xếp Merge Sort - Viblo

Trang chủ » độ Phức Tạp Thuật Toán Merge Sort » Thuật Toán Sắp Xếp Merge Sort - Viblo

Có thể bạn quan tâm

  • Báo cáo
  • Thêm vào series của tôi

Bài đăng này đã không được cập nhật trong 5 năm

Merge Sort

Đây là một trong các thuật toán sắp xếp cơ bản mà sinh viên thường bị hỏi khi đi phỏng vấn, cùng với các thuật toán sắp xếp khác như: quick sort, heap sort, ...

Merge sort sử dụng kĩ thuật chia để trị cho việc sắp xếp. Merge sort gồm 2 công đoạn:

  • Đầu tiên nó chia dãy cần sắp xếp thành 2 nửa.
  • Sau đó gộp 2 dãy đã được sắp xếp lại thành một.

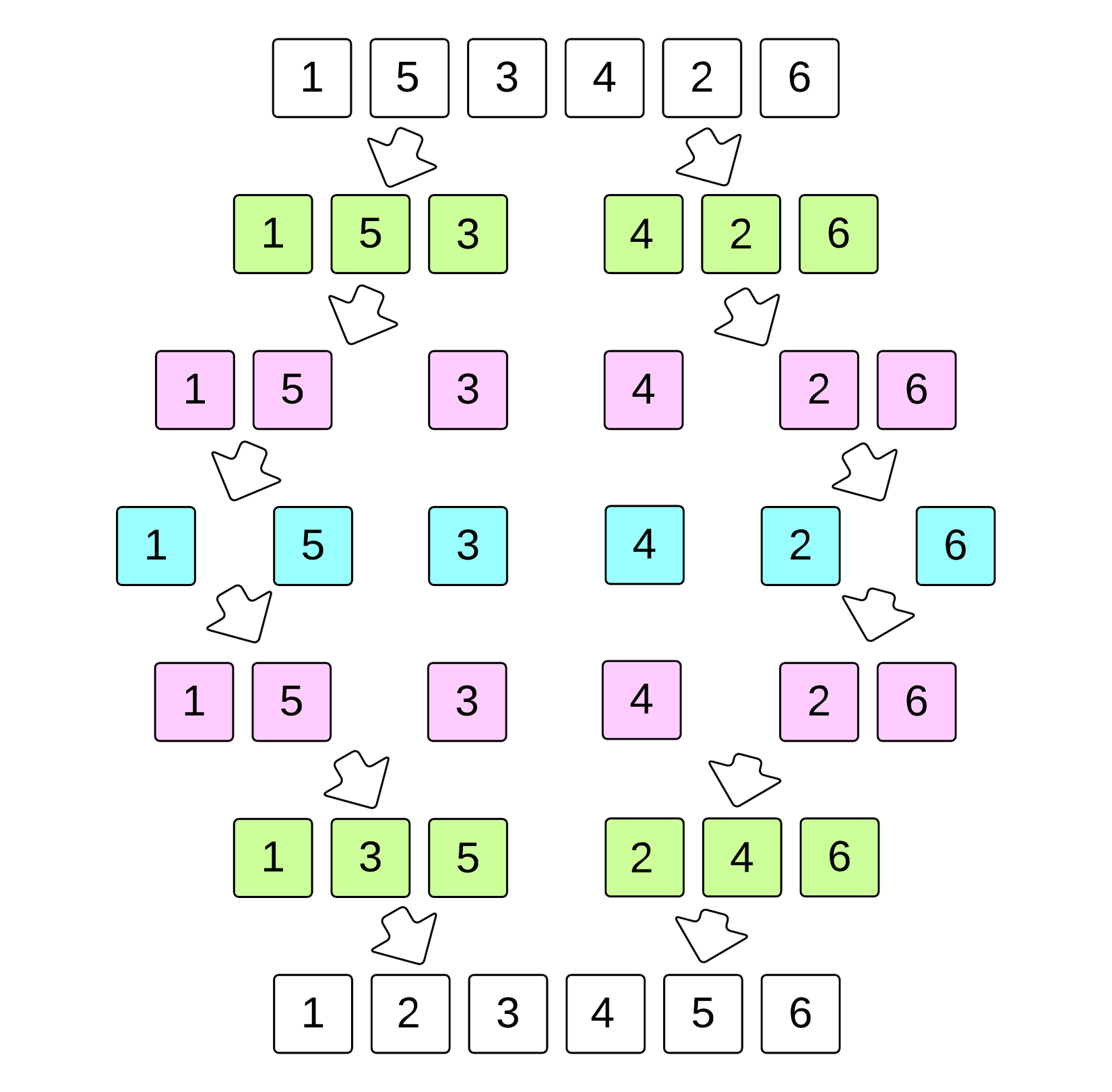
def merge arr, left, mid, right # create temp arrays tempL = [] tempR = [] # copy data to temp arrays for i in left..mid do tempL.push(arr[i]) end for i in mid+1..right do tempR.push(arr[i]) end # merge 2 temp arrays i = 0 j = 0 k = left while i < tempL.length && j < tempR.length if tempL[i] <= tempR[j] arr[k] = tempL[i] i += 1 else arr[k] = tempR[j] j += 1 end k += 1 end while i < tempL.length arr[k] = tempL[i] i += 1 k += 1 end while j < tempR.length arr[k] = tempR[j] j += 1 k += 1 end end def mergesort arr, left, right if left < right mid = (left + right) / 2 mergesort arr, left, mid mergesort arr, mid + 1, right merge arr, left, mid, right end end

Độ phức tạp thời gian trong trường hợp xấu nhất, tốt nhất, trung bình của Merge Sort đều là O(nlogn), điều này làm cho Merge Sort tỏ ra khá hiệu quả. Merge sort là một lựa chọn khi cần một thuật toán để sắp xếp có tính ổn định, khác với quick sort, không ổn định cho lắm. Nhược điểm của merge sort có thể kể đến như không hiệu quả lắm về mặt không gian, khi độ phức tạp không gian trong trường hợp xấu nhất là O(n), trong khi của quick sort là O(1)

Nguồn tham khảo : wikipedia.

Algorithm Programming sorting

All rights reserved

  • Báo cáo
  • Thêm vào series của tôi

Từ khóa » độ Phức Tạp Thuật Toán Merge Sort