Tìm Số Tự Nhiên N để Phân Số A = 8n + 1934n + 3: A) Có Giá Trị Là Số

Lời giải của Tự Học 365

Giải chi tiết:

a) \(A = \frac{{8n + 193}}{{4n + 3}} = \frac{{2.4n + 2.3 + 187}}{{4n + 3}}\)\( = \frac{{2.\left( {4n + 3} \right) + 187}}{{4n + 3}} = 2 + \frac{{187}}{{4n + 3}}\)

Để \(A \in \mathbb{N}\) thì  \(\frac{{187}}{{4n + 3}} \in \mathbb{N} \Rightarrow 4n + 3 \in U\left( {187} \right) = \left\{ {1;\,\,11;\,\,\,17;\,\,187} \right\}\) .

Vì \(n \in \mathbb{N} \Rightarrow 4n + 3 \in \left\{ {11;\,\,17;\,\,187} \right\}.\)  Ta có bảng sau:

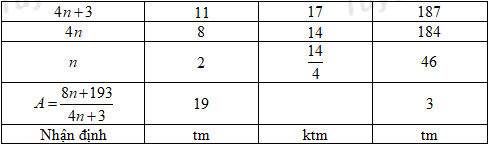
Vậy với \(n \in \left\{ {2;\,\,46} \right\}\) thì phân số \(A = \frac{{8n + 193}}{{4n + 3}}\) nhận giá trị là số tự nhiên.

b) Gọi \(d\) là ước nguyên tố của \(8n + 193\) và \(4n + 3\).

Ta có: \(\left\{ \begin{array}{l}8n + 193\,\, \vdots \,\,d\\4n + 3\,\, \vdots \,\,d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}8n + 193\,\, \vdots \,\,d\\2.\left( {4n + 3\,} \right)\, \vdots \,\,d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}8n + 193\,\, \vdots \,\,d\\8n + 6\,\, \vdots \,\,d\end{array} \right.\)\( \Rightarrow \left( {8n + 193} \right) - \left( {8n + 6} \right)\,\, \vdots \,\,d\)

\( \Rightarrow 8n + 193 - 8n - 6\,\, \vdots \,\,d\)

\( \Rightarrow 187\,\, \vdots \,\,d\) mà \(d\) là số nguyên tố nên \(d \in \left\{ {11;\,\,17} \right\}.\)

+) Với \(d = 11 \Rightarrow 4n + 3\,\, \vdots \,\,11 \Rightarrow 4n + 3 - 11\,\, \vdots \,\,11\)\( \Rightarrow 4n - 8\,\, \vdots \,\,11 \Rightarrow 4.\left( {n - 2} \right)\,\, \vdots \,\,11\)

\( \Rightarrow n - 2\,\, \vdots \,\,11 \Rightarrow n = 11k + 2\,\,\left( {k \in \mathbb{N}} \right)\)

+) Với \(d = 17 \Rightarrow 4n + 3\,\, \vdots \,\,17 \Rightarrow 4n + 3 + 17\,\, \vdots \,\,17\)\( \Rightarrow 4n + 20\,\, \vdots \,\,17 \Rightarrow 4.\left( {n + 5} \right)\,\, \vdots \,\,17\)

\( \Rightarrow n + 5\,\, \vdots \,\,17 \Rightarrow n + 5 = 17m \Rightarrow n = 17m - 5\,\,\left( {m \in {\mathbb{N}^*}} \right)\)

\( \Rightarrow \) Phân số \(A = \frac{{8n + 193}}{{4n + 3}}\) rút gọn được khi \(n = 11k + 2\,\,\left( {k \in \mathbb{N}} \right)\) và \(n = 17m - 5\,\,\left( {m \in {\mathbb{N}^*}} \right)\)

Vậy \(n \ne 11k + 2\,\,\left( {k \in \mathbb{N}} \right)\) và \(n \ne 17m - 5\,\,\left( {m \in {\mathbb{N}^*}} \right)\) thì \(A = \frac{{8n + 193}}{{4n + 3}}\) là phân số tối giản.

c) Để phân số \(A = \frac{{8n + 193}}{{4n + 3}}\) rút gọn được thì \(n = 11k + 2\,\,\left( {k \in \mathbb{N}} \right)\) và \(n = 17m - 5\,\,\left( {m \in {\mathbb{N}^*}} \right)\).

Vì \(n\) trong khoảng từ \(150\) đến \(170\) nên:

+) \(150 < n < 170 \Rightarrow 150 < 11k + 2 < 170\)\( \Rightarrow 148 < 11k < 168\,\,\left( {k \in \mathbb{N}} \right)\)\( \Rightarrow k \in \left\{ {14;15} \right\} \Rightarrow n \in \left\{ {156;\,\,167} \right\}\)

+) \(150 < n < 170 \Rightarrow 150 < 17m - 5 < 170\)\( \Rightarrow 155 < 17m < 175\,\,\left( {m \in \mathbb{N}} \right)\)\( \Rightarrow m = 10 \Rightarrow n = 165\)

Vậy \(n \in \left\{ {156;\,165;\,167} \right\}\).