Tìm Số Tự Nhiên \(n\) để Phân Số \(A = \frac{{8n + 193}}{{4n + 3}}\)

Câu hỏi số 384205: Vận dụng

Tìm số tự nhiên \(n\) để phân số \(A = \frac{{8n + 193}}{{4n + 3}}\):

a) Có giá trị là số tự nhiên.

b) Là phân số tối giản.

c) Với giá trị nào của \(n\) trong khoảng từ \(150\) đến \(170\) thì phân số \(A\) rút gọn được.

Quảng cáo

Xem lời giải Câu hỏi:384205 Phương pháp giải

a) Phân số có giá trị là số tự nhiên thì phân số đó có tử và mẫu cùng dấu, tử số chia hết cho mẫu số.

b) Phân số là phân số tối giản thì phân số đó có tử và mẫu có ước chung là \(1\) và \( - 1.\)

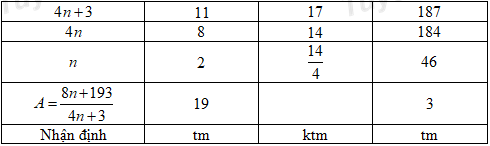
Giải chi tiết

a) \(A = \frac{{8n + 193}}{{4n + 3}} = \frac{{2.4n + 2.3 + 187}}{{4n + 3}}\)\( = \frac{{2.\left( {4n + 3} \right) + 187}}{{4n + 3}} = 2 + \frac{{187}}{{4n + 3}}\)

Để \(A \in \mathbb{N}\) thì  \(\frac{{187}}{{4n + 3}} \in \mathbb{N} \Rightarrow 4n + 3 \in U\left( {187} \right) = \left\{ {1;\,\,11;\,\,\,17;\,\,187} \right\}\) .

Vì \(n \in \mathbb{N} \Rightarrow 4n + 3 \in \left\{ {11;\,\,17;\,\,187} \right\}.\)  Ta có bảng sau:

Vậy với \(n \in \left\{ {2;\,\,46} \right\}\) thì phân số \(A = \frac{{8n + 193}}{{4n + 3}}\) nhận giá trị là số tự nhiên.

b) Gọi \(d\) là ước nguyên tố của \(8n + 193\) và \(4n + 3\).

Ta có: \(\left\{ \begin{array}{l}8n + 193\,\, \vdots \,\,d\\4n + 3\,\, \vdots \,\,d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}8n + 193\,\, \vdots \,\,d\\2.\left( {4n + 3\,} \right)\, \vdots \,\,d\end{array} \right. \Rightarrow \left\{ \begin{array}{l}8n + 193\,\, \vdots \,\,d\\8n + 6\,\, \vdots \,\,d\end{array} \right.\)\( \Rightarrow \left( {8n + 193} \right) - \left( {8n + 6} \right)\,\, \vdots \,\,d\)

\( \Rightarrow 8n + 193 - 8n - 6\,\, \vdots \,\,d\)

\( \Rightarrow 187\,\, \vdots \,\,d\) mà \(d\) là số nguyên tố nên \(d \in \left\{ {11;\,\,17} \right\}.\)

+) Với \(d = 11 \Rightarrow 4n + 3\,\, \vdots \,\,11 \Rightarrow 4n + 3 - 11\,\, \vdots \,\,11\)\( \Rightarrow 4n - 8\,\, \vdots \,\,11 \Rightarrow 4.\left( {n - 2} \right)\,\, \vdots \,\,11\)

\( \Rightarrow n - 2\,\, \vdots \,\,11 \Rightarrow n = 11k + 2\,\,\left( {k \in \mathbb{N}} \right)\)

+) Với \(d = 17 \Rightarrow 4n + 3\,\, \vdots \,\,17 \Rightarrow 4n + 3 + 17\,\, \vdots \,\,17\)\( \Rightarrow 4n + 20\,\, \vdots \,\,17 \Rightarrow 4.\left( {n + 5} \right)\,\, \vdots \,\,17\)

\( \Rightarrow n + 5\,\, \vdots \,\,17 \Rightarrow n + 5 = 17m \Rightarrow n = 17m - 5\,\,\left( {m \in {\mathbb{N}^*}} \right)\)

\( \Rightarrow \) Phân số \(A = \frac{{8n + 193}}{{4n + 3}}\) rút gọn được khi \(n = 11k + 2\,\,\left( {k \in \mathbb{N}} \right)\) và \(n = 17m - 5\,\,\left( {m \in {\mathbb{N}^*}} \right)\)

Vậy \(n \ne 11k + 2\,\,\left( {k \in \mathbb{N}} \right)\) và \(n \ne 17m - 5\,\,\left( {m \in {\mathbb{N}^*}} \right)\) thì \(A = \frac{{8n + 193}}{{4n + 3}}\) là phân số tối giản.

c) Để phân số \(A = \frac{{8n + 193}}{{4n + 3}}\) rút gọn được thì \(n = 11k + 2\,\,\left( {k \in \mathbb{N}} \right)\) và \(n = 17m - 5\,\,\left( {m \in {\mathbb{N}^*}} \right)\).

Vì \(n\) trong khoảng từ \(150\) đến \(170\) nên:

+) \(150 < n < 170 \Rightarrow 150 < 11k + 2 < 170\)\( \Rightarrow 148 < 11k < 168\,\,\left( {k \in \mathbb{N}} \right)\)\( \Rightarrow k \in \left\{ {14;15} \right\} \Rightarrow n \in \left\{ {156;\,\,167} \right\}\)

+) \(150 < n < 170 \Rightarrow 150 < 17m - 5 < 170\)\( \Rightarrow 155 < 17m < 175\,\,\left( {m \in \mathbb{N}} \right)\)\( \Rightarrow m = 10 \Rightarrow n = 165\)

Vậy \(n \in \left\{ {156;\,165;\,167} \right\}\).