Tìm X Thuộc Z để A=x+1/x-1 Là Số Nguyên

Trang chủ » để X » Tìm X Thuộc Z để A=x+1/x-1 Là Số Nguyên

Có thể bạn quan tâm

Tất cả Toán học Vật Lý Hóa học Văn học Lịch sử Địa lý Sinh học Giáo dục công dân Tin học Tiếng anh Công nghệ Khoa học Tự nhiên Lịch sử và Địa lý D Dung Nguyen Hỏi từ APP VIETJACK đã hỏi trong Lớp 7 Toán học · 16:13 22/06/2021 Báo cáo

Tìm x thuộc z để A=x+1x-1 là số nguyên

Trả Lời Hỏi chi tiết Trả lời trong APP VIETJACK ...Xem câu hỏi chi tiết

Quảng cáo

3 câu trả lời 5889

Len Nguyễn 3 năm trước

M

L

1 bình luận D Dung Nguyen · 3 năm trước Cj ơi em vt nhầm ạ đề bài là tìm x thuộc z để x-1/x+1 là số nguyên ạ Đăng nhập để hỏi chi tiết H Hằng 3 năm trước

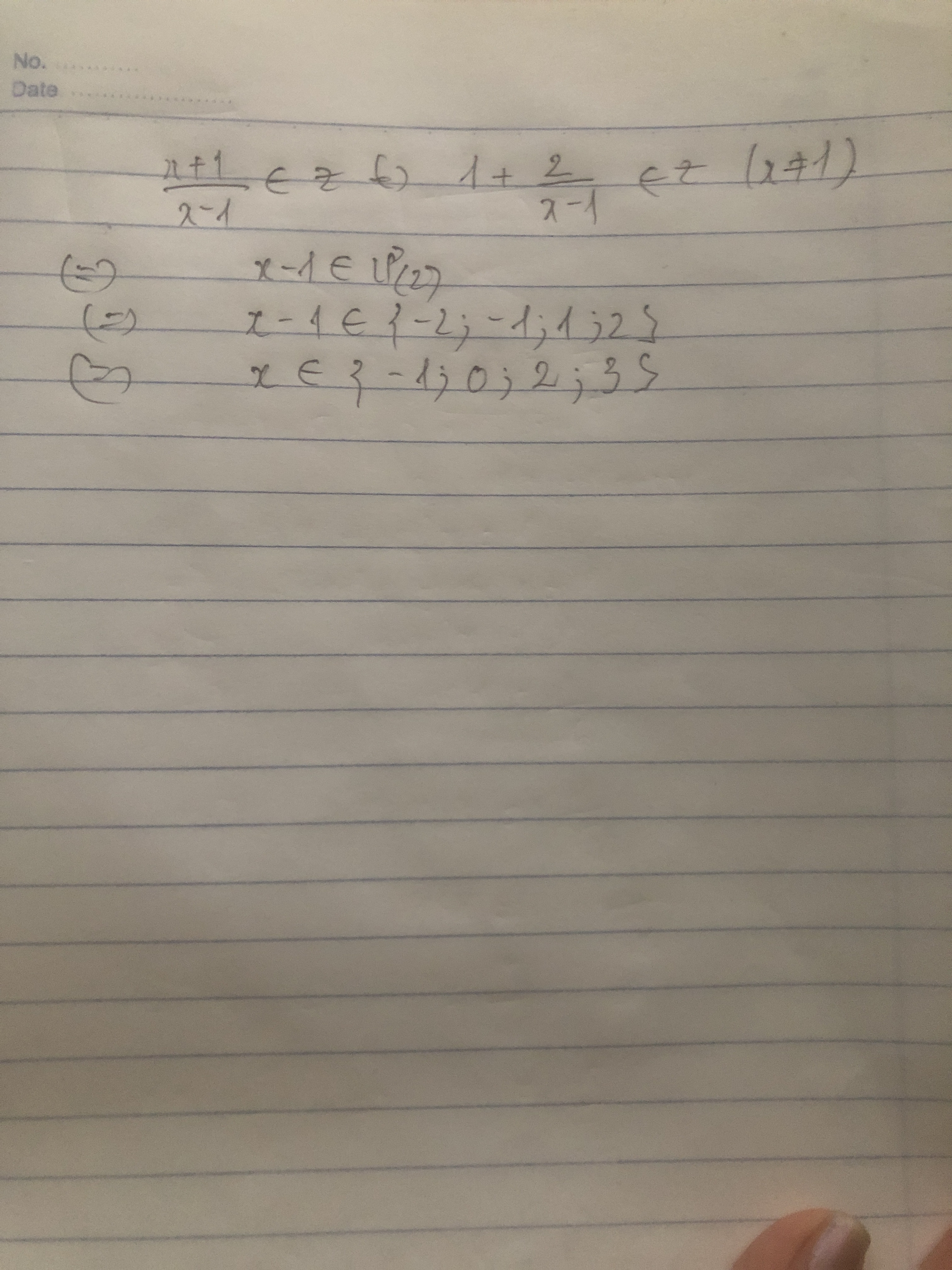
\[\begin{array}{l}A = \frac{{x + 1}}{{x - 1}}\\dk:x \ne 1\\A = \frac{{x - 1 + 2}}{{x - 1}}\\ = \frac{{x - 1}}{{x - 1}} + \frac{2}{{x - 1}}\\ = 1 + \frac{2}{{x - 1}}\\De:A \in Z =  > \frac{2}{{x - 1}} \in Z\\ \Leftrightarrow (x - 1) \in U(2) = \{  - 2; - 1;1;2\} \\ =  > x \in \{  - 1;0;2;3\} (tm)\end{array}\]

0 bình luận Đăng nhập để hỏi chi tiết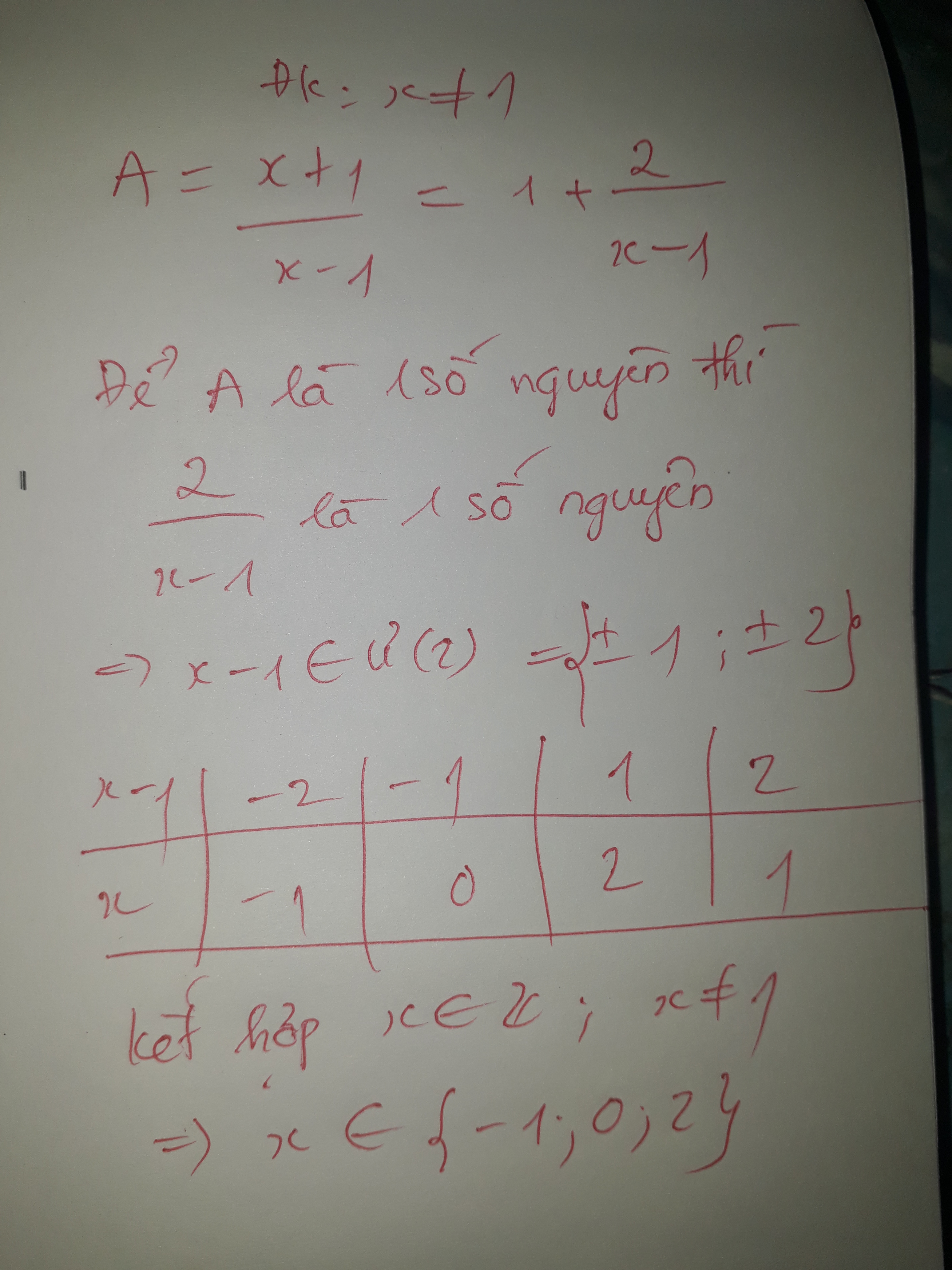 Đoàn Thị Xuân 3 năm trước

X

0 bình luận Đăng nhập để hỏi chi tiết

Quảng cáo

Câu hỏi hot cùng chủ đề

  • Cho ΔABC có AB < AC. Kẻ tia phân giác AD của BAC^ (D thuộc BC). Trên cạnh AC lấy điểm E sao cho AE = AB, trên tia AB lấy điểm F sao cho AF = AC. Chứng minh rằng:

    a)  ΔBDF=ΔEDC;

    b) F, D E thẳng hàng;

    c)  AD⊥FC

    Trả lời (22) Xem đáp án » 19 124311

  • Điểm cách đều ba cạnh của tam giác là:

    A. Giao điểm của ba đường cao

    B. Giao điểm của ba đường trung trực

    C. Giao điểm của ba đường trung tuyến

    D. Giao điểm của ba đường phân giác

    Trả lời (224) Xem đáp án » 9 72260

  • Cho ∆ABC, M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME=MA. Chứng minh rằng:a/ AC=EB   và  AC //  BEb/ Gọi I là một điểm trên AC, K là một điểm trên EB sao cho: AI=EK. Chứng minh: I, M, K  thẳng hàng.c/  Từ E kẻ EH ⊥ BC (H ∈ BC). Biết góc HBE^ bằng 50°; MEB^ bằng 25°, tính các góc HEM^  và BME^ ?

    Trả lời (12) Xem đáp án » 6 65237

  • Cho tam giác ABC vuông tại A, đường phân giác BE. Kẻ EH vuông góc với BC (H thuộc BC). Gọi K giao điểm của AB và HE. Chứng minh rằng:

    a, ∆ABE=∆HBE

    b, BE là đường trung trực của đoạn thẳng AH

    c, EK=EC

    d, AE<EC.

Từ khóa » để X