Trong Không Gian Với Hệ Tọa độ Oxyz, Cho Mặt Cầu (S ...

1. Hệ tọa độ trong không gian

1.1. Tọa độ của điểm và của vecto

1.1.1. Hệ tọa độ

Trong không gian, xét ba trục tọa độ x’Ox; y’Oy; z’Ozvuông góc với nhau từng

đôi một và chung một điểm gốc O. Gọi i→;j→;k→ lần lượt là các vectơ đơn vị, trên các trục x’Ox; y’Oy; z’Oz.

Hệ ba trục như vậy gọi là hệ trục tọa độ Đề- các vuông góc Oxyz trong không gian,

hay đơn giản gọi là hệ trục tọa độ Oxyz.

Điểm O được gọi là gốc tọa độ.

Các mặt phẳng (Oxy); (Oyz); (Ozx) đôi một vuong góc với nhau được gọi là các mặt phẳng tọa độ.

Không gian với hệ tọa độ Oxyz còn gọi là không gian Oxyz.

- Vì i→;j→;k→ là các vecto đơn vị đôi một vuông góc với nhau nên:

i→2=j→2=k→2=  1.

1.1.2. Tọa độ của một điểm

- Trong không gian Oxyz, cho một điểm M tùy ý. Vì ba vecto i→;j→;k→ không đồng

phẳng nên có một bộ ba số (x; y; z) duy nhất sao cho:

O⁢M→=x.i→⁢ +y.j→+z.k→

- Ngược lại, với bộ ba số (x; y; z) ta có một điểm M duy nhất trong không gian thỏa mãn hệ thức O⁢M→=x.i→+y.j→+z.k→.

- Ta gọi bộ ba số (x; y; z) là tọa độ của điểm M đối với hệ trục tọa độ Oxyz đã cho và viết: M = ( x; y; z) hoặc M (x; y; z).

1.1.3. Tọa độ của vecto

- Trong không gian Oxyz cho vecto a→, khi đó luôn tồn tại duy nhất bộ ba số (a1; a2 ; a3) sao cho a→=a1.i→+a2.j→+a3.k→.

Ta gọi bộ ba số (a1; a2 ; a3) là tọa độ của vecto đối với hệ tọa độ Oxyz cho trước a→ và viết a→ = (a1; a2 ; a3) hoặc a→(a1; a2 ; a3).

- Nhận xét : Trong hệ tọa độ Oxyz, tọa độ của điểm M chính là tọa độ của vecto O⁢M→.

Ta có: M(x; y; z) ⇔O⁢M→⁢(x;y;z)

1.2. Biểu thức tọa độ của các phép toán của vecto

- Định lí: Trong không gian Oxyz, cho hai vecto

a→⁢⁢ =(a1;a2;a3),b→⁢⁢ =(b1;b2;b3),k∈⁢R, ta có:

a) a→+b→=(a1+b1;a2+b2;a3+b3)

b) a→-b→=(a1-b1;a2-b2;a3-b3);

c) k⁢a→=(k⁢a1;k⁢a2;k⁢a3).

Ví dụ 1. Cho u→⁢(2;-3; 4);v→⁢(  4;-2;0)

a) Tính u→+v→;

b) 2⁢v→;

c) u→-2⁢v→.

Lời giải:

a) u→+v→=(2+  4;-3-2; 4+0)=(6;-5;  4) ;

b) Ta có: 2⁢v→ = ( 2.4; 2. (-2); 2.0) = ( 8; - 4; 0).

c) Ta có: u→-2⁢v→ = ( 2 – 8; -3 + 4; 4 - 0) = (- 6; 1; 4)

- Hệ quả:

a) Cho hai vecto a→⁢ =(a1;a2;a3),b→⁢ =(b1;b2;b3), ta có:

a→⁢=b→⇔{a1=b1a2=b2a3=b3.

b) Vecto 0→ có tọa độ ( 0; 0; 0).

c) Với b→≠0→ thì hai vecto a→;b→ cùng phương khi và chỉ khi tồn tại số k sao cho:

a→ =kb→(k∈R)

⇔{a1=kb1a2=kb2a3=kb3⇔a1b1=a2b2=a3b3,(b1,b2,b3≠0)

d) Cho A⁢(xA;yA;zA),B⁢(xB;yB;zB)

+ A⁢B→⁢ =(xB-xA;yB-yA;zB-zA)

+ Toạ độ trung điểm M của đoạn thẳng AB: M⁢(xA+xB2;yA+yB2;zA+zB2)

Ví dụ 2. Cho u→⁢(2⁢m; 3;-1);v→⁢(4;  3;n-2). Tìm m và n để u→=v→

Lời giải:

Để u→=v→

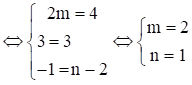
Vậy m = 2 và n = 1.

Ví dụ 3. Các cặp vecto sau có cùng phương không?

a) u→⁢(  2;3;7);v→⁢(-4;-6;  14);

b) a→⁢( 1; 0;  2);b→⁢(-3;0;-6).

Lời giải:

a) Ta thấy 2-4=3-6≠714

Do đó, hai vecto trên không cùng phương.

b) Ta thấy: b→=-3⁢a→ nên hai vecto trên cùng phương.

Ví dụ 4. Cho hai điểm A( - 3; 4; 0) và B( -1; 0; 8).

a) Tính A⁢B→;

b) Tìm tọa độ trung điểm M của AB.

Lời giải:

a) Ta có: A⁢B→ = ( -1 + 3; 0 - 4; 8 -0) = ( 2; -4; 8).

b)Tọa độ trung điểm M của AB là:

{xM=-3+(-1)2=-2yM=4+ 02=2zM=0+  82= 4⇒M⁢(-2;2;4)

1.3. Tích vô hướng.

1.3.1. Biểu thức tọa độ của tích vô hướng.

- Định lí:

Trong không gian Oxyz, tích vô hướng của hai vecto a→⁢⁢ =(a1;a2;a3),b→⁢⁢ =(b1;b2;b3) được xác định bởi công thức:

a→.b→=a1.b1+a2.b2+a3.b3

Ví dụ 5. Cho a→⁢(1;-3;4);b→⁢(1;2;1). Tính a→.b→?

Lời giải:

Ta có: a→.b→ =1.1 + ( -3). 2 + 4.1 = -1

1.3.2. Ứng dụng

a) Độ dài của một vecto.

Cho vecto a→⁢ =(a1;a2;a3).

Ta biết rằng: |a→|2=a→2 hay |a→|=a→2. Do đó, |a→|=a12+a22+a22

b) Khoảng cách giữa hai điểm.

Trong khong gian Oxyz, cho hai điểm A(xA ; yA ; zA)

và B(xB; yB ; zB). Khi đó, khoảng cách giữa hai điểm A và B chính là độ dài của

vecto A⁢B→. Do đó, ta có:

A⁢B=|A⁢B→|=(xB-xA)2+(yB-yA)2+(zB-zA)2.

c) Góc giữa hai vecto.

Nếu φ là góc góc giữa hai vecto a→=(a1;a2;a3) và b→=(b1;b2;b3) với a→;b→≠0→ thì cos⁡(a→,b→)=a→.b→|a→|.|b→|=a1⁢b1+a2⁢b2+a3⁢b3a12+a22+a32.b12+b22+b32

Từ đó, suy ra a→⁢⊥b→⇔a1⁢b1+a2⁢b2+a3⁢b3=0

Ví dụ 6. Cho tam giác ABC có A(2; 3; 1); B( 2; 1; 0); C( 0; -1; 2).

a) Tính AB; AC

b) Tính cosin của góc A.

Lời giải:

a) Ta có:

A⁢B=(2-2)2+(1-3)2+(0-1)2=5 AC=(0-2)2+(-1-3)2+(2-1)2=21

b) Ta có: A⁢B→⁢(0;-2;-1);A⁢C→⁢(-2;-4;1)

Cosin của góc A là:

cos⁡A=cos⁡(A⁢B→;A⁢C→)=0.(-2)+(-2).(-4)+(-1)⁢.15.21=7105

1.4. Phương trình mặt cầu

- Định lí.

Trong không gian Oxyz, mặt cầu (S) tâm I(a; b; c) bán kính r có phương trình là:

( x – a)2 + (y – b)2 + (z – c)2 = r2

- Nhận xét. Phương trình mặt cầu nói trên có thể viết dưới dạng:

x2 + y2 + z2 – 2ax – 2by – 2cz + d = 0 với d = a2 + b2 + c2 – r2

Từ đó, ta chứng minh được rằng phương trình dạng:

x2 + y2 + z2 + 2Ax + 2By + 2Cz + D = 0 với điều kiện A2 + B2 + C2 – D > 0 là phương trình mặt cầu có tâm I( -A; -B; - C) có bán kính r=A2+B2+C2-D.

Ví dụ 7. Tìm tâm và bán kính của mặt cầu có phương trình sau đây:

a) x2 + y2 + z2 – 4x + 2y - 1 = 0;

b) x2 + y2 + z2 – 8x – 2y + 2z + 2 = 0

Lời giải:

a) Ta có:a = 2; b = -1; c = 0; d = -1

Tâm mặt cầu là I(2; -1; 0) và bán kính R=22+(-1)2+ 02