Trong Không Gian Với Hệ Trục Tọa độ Oxyz, Cho điểm M(1;2;5). Số Mặt ...

Tất cả Toán học Vật Lý Hóa học Văn học Lịch sử Địa lý Sinh học Giáo dục công dân Tin học Tiếng anh Công nghệ Khoa học Tự nhiên Lịch sử và Địa lý Trâm Anh đã hỏi trong Lớp 12 Toán học · 09:30 29/08/2020 Chương 3: Phương pháp tọa độ trong không gian Theo dõi Báo cáo

Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;2;5). Số mặt phẳng đi qua M và cắt các trục Ox, Oy, Oz tại A, B, C sao cho OA = OB = OC (A, B, C không trùng với gốc tọa độ O) là:

A.8

B.3

C.4

D.1

Trả Lời Hỏi câu khác Hỏi chi tiết ...Xem thêm

Quảng cáo

1 câu trả lời 3173

Phương Anh 5 năm trước

Đáp án C

Phương pháp

+) Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0)viết phương trình mặt phẳng (P) đi qua A, B, C dạng đoạn chắn.M∈(P)=> Thay tọa độ điểm M vào phương trình mặt phẳng (P).

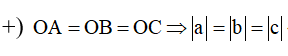
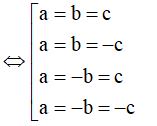
+) Ứng với mỗi trường hợp tìm các ẩn a, b, c tương ứng

Cách giải

Gọi A(a;0;0), B(0;b;0), C(0;0;c) (a, b, c ≠ 0) khi đó phương trình mặt phẳng đi qua A, B, C là

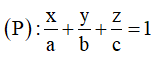
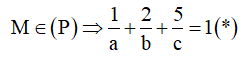
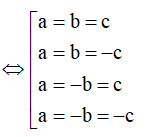
TH1: a=b=c thay vào (*) có

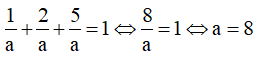
TH2: a=b=-c thay vào (*) có

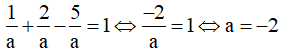
TH3: a=-b=c thay vào (*) có

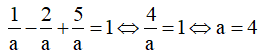
TH4: a=-b=-c thay vào (*) có

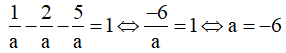
Vậy có 4 mặt phẳng thỏa mãn.

...Xem thêm 0 bình luận Đăng nhập để hỏi chi tiết

Quảng cáo

Bạn muốn hỏi bài tập?

Đặt câu hỏi

Câu hỏi hot cùng chủ đề

• Trong không gian với hệ tọa độ Oxyz, trục Oycó phương trình là

  

  

  

  

  Trả lời (2) Xem đáp án » 69193

• Phương trình mặt cầu đường kính AB với A(-1;2;5), B(3;-2;1) là

  A. (x+1)2+y2+(z+3)2=12

  B. (x+1)2+y2+(z+3)2=3

  C. (x-1)2+y2+(z-3)2=12

  D. (x-1)2+y2+(z-3)2=48

  Trả lời (2) Xem đáp án » 67754

• Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có AB⇀= (-3;0;4), AC⇀=(5;-2;4).

  Độ dài trung tuyến AM là:

  

  

  

  

  Trả lời (2) Xem đáp án » 30887

• Trong không gian Oxyz, cho đường thẳng d:x-11=y-1=z-21và mặt phẳng (P): 2x-y-2z+1=0. Đường thẳng nằm trong (P), cắt và vuông góc với d có phương trình là:

  

  

  

  

  Trả lời (1) Xem đáp án » 29163

• Trong không gian Oxyz, mặt cầu tâm I(-1;2;-3) và đi qua điểm A(2;0;0) có phương trình là:

  A. (x+1)2+(y-2)2+(z-3)2=22

  B. (x+1)2+(y-2)2+(z+3)2=11

  C. (x+1)2+(y-2)2+(z+3)2=22

  D. (x-1)2+(y+2)2+(z-3)2=22

  Trả lời (1) Xem đáp án » 28182

• Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(1;2;-1); B(2;-1;3); C(-3;5;1). Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.

  

  

  

  

  Trả lời (1) Xem đáp án » 21634

• Trong không gian Oxyz, cho điểm I(1;-2;3). Viết phương trình mặt cầu tâm I, cắt trục Ox tại 2 điểm A, B sao cho AB=23

  A. (x-1)2+(y+2)2+(z-3)2=16

  B. (x-1)2+(y+2)2+(z-3)2=20

  C. (x-1)2+(y+2)2+(z-3)2=25

  D. (x-1)2+(y+2)2+(z-3)2=9

  Trả lời (1) Xem đáp án » 20871

• Trong không gian Oxyz, cho mặt cầu (S) có tâm I(1;-2;-3) và đi qua điểm M(-1;0;-2). Phương trình của mặt cầu (S) là:

  A. (x - 1)2 + (y + 2)2 + (z + 3)2 = 3

  B. (x + 1)2 + (y - 2)2 + (z - 3)2 = 9

  C. (x + 1)2 + (y - 2)2 + (z - 3)2 = 3

  D. (x - 1)2 + (y + 2)2 + (z + 3)2 = 9

  Trả lời (1) Xem đáp án » 18366

• Trong không gian Oxyz, cho hai điểm A(-1;2;3)và B(3;-2;1). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là

  

  

  

  

  Trả lời (1) Xem đáp án » 16889

• Mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn khi ?

  A. Khoảng cách từ tâm đến mặt phẳng bằng bán kính

  B. Khoảng cách từ tâm đến mặt phẳng nhỏ hơn bán kính

  C. Khoảng cách từ tâm đến mặt phẳng lớn hơn bán kính

  D. Mặt phẳng là tiếp diện của mặt cầu

  Trả lời (1) Xem đáp án » 16257

Quảng cáo

Đặt câu hỏi ngay Thành viên hăng hái nhất trong tuần

• zytera 1325 điểm
• Dương Nguyễn 960 điểm
• 보고 싶어요 855 điểm
• 돈이없다 💸😭 815 điểm
• 우옌 ✨ 790 điểm
• `d.` 635 điểm
• ภ ภgứค ςả ๓ắt t 590 điểm
• `color{blue}text{HuyTùng.` 555 điểm
• ౨ৎ𝘉ắ𝘱ت𝘭𝘶ộ𝘤تđê⋅˚₊‧ ଳ⋆.࿔*:･🌽 540 điểm
• 주디 홉스닉주디🥵👍 520 điểm
• ‧₊˚✩ ₊˚🎧⊹♡≽☁˚˖ִ໋🌷͙֒✧˚.🎀༘⋆⋅♡👾đẹρ-†®åî⋆⭒💫 435 điểm
• Ngọc Linh hay nói linh tinh 385 điểm
• Kiều Anh 350 điểm
• 누가 고철을 팔고 싶어할까요🗑️🗑️ 345 điểm
• Bích Hồng 345 điểm

Xem thêm Rút gọn

Bài viết mới nhất Lớp 12

• Dao động điều hòa ( Lý thuyết + 50 bài tập có lời giải ) 3 năm trước 5939
• Trắc nghiệm Công nghệ 12 Bài 28 có đáp án năm 2021 – 2022 4 năm trước 4095
• Trắc nghiệm Công nghệ 12 Bài 26 có đáp án năm 2021 – 2022 4 năm trước 3998
• Trắc nghiệm Công nghệ 12 Bài 25 có đáp án năm 2021 – 2022 4 năm trước 4205
• Trắc nghiệm Công nghệ 12 Bài 23 có đáp án năm 2021 – 2022 4 năm trước 4893

Xem thêm » Gửi báo cáo thành công!

Thông báo

× × Trải nghiệm miễn phí Hỏi đáp với App VietJack ! Tiếp tục sử dụng web! Đăng nhập vào hệ thống × Tài khoản Google Lưu mật khẩu Bạn quên mật khẩu? Đăng nhập Bạn chưa có tài khoản? Đăng ký ngay Đăng ký vào hệ thống × Tài khoản Google Đăng ký Bạn đã có tài khoản? Đăng nhập ngay Khôi phục tài khoản × Khôi phục Bạn đã có tài khoản? Đăng nhập ngay Đặt câu hỏi