Trong Mặt Phẳng Tọa độ Oxy. Tìm Tọa độ Trực Tâm H Và Tọa ... - Hoc24
Có thể bạn quan tâm
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
 Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
- Lê Hà My
Trong mặt phẳng tọa độ Oxy. Tìm tọa độ trực tâm H và tọa độ chân đường cao A' vẽ từ A trong tam giác ABC với A(-5;6), B(-4; -1), C(4;3)
Xem chi tiết Lớp 10 Toán Ôn tập chương I 2 0 Gửi Hủy
Gửi Hủy  đề bài khó wá
đề bài khó wá  6 tháng 4 2020 lúc 0:04
6 tháng 4 2020 lúc 0:04 b/ Gọi A' có tọa độ là (x;y) ta có : \(\left\{{}\begin{matrix}\overrightarrow{AA'}=\left(x+5,y-6\right)\\\overrightarrow{BC}=\left(8,4\right)\\\overrightarrow{BA'}=\left(x+4;y+1\right)\end{matrix}\right.\)
Từ giả thiết có A' là hình chiếu của A trên BC nếu \(AA'\perp BC\) và B,A',C thẳng hàng
\(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AA'}.\overrightarrow{BC}=0\left(1\right)\\\overrightarrow{BA'}=k\overrightarrow{BC}\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow8\left(x+5\right)+4\left(y-6\right)=0\Leftrightarrow8x+4y+16=0\)
\(\left(2\right)\Leftrightarrow\frac{x+4}{8}=\frac{y+1}{4}\Leftrightarrow4x-8y+8=0\)
Giải hệ ta được x = -2 và y = 0
=> A'=(-2;0)
Đúng 0 Bình luận (0) Khách vãng lai đã xóa Gửi Hủy
Gửi Hủy  đề bài khó wá
đề bài khó wá  5 tháng 4 2020 lúc 23:50
5 tháng 4 2020 lúc 23:50 
 Gửi Hủy
Gửi Hủy 
- Đặng Thị Phương Anh
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có trực tâm H(-1;3), tâm đường tròn ngoại tiếp I(-3;3), chân đường cao kẻ từ đỉnh A là điểm K(-1;1). Tìm tọa độ các đỉnh A, B, C
Xem chi tiết Lớp 10 Toán Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG 1 0 Gửi Hủy
Gửi Hủy  Nguyễn Tiến Mạnh 7 tháng 4 2016 lúc 9:11
Nguyễn Tiến Mạnh 7 tháng 4 2016 lúc 9:11 B A D D C H K M I
Ta có \(HK\perp BC,K\in BC;\overrightarrow{HK}=\left(0;-2\right)\Rightarrow y-1=0\)
Gọi M là trung điểm của BC ta có phương trình \(x+3=0;M=IM\cap BC\Rightarrow M\left(-3;1\right)\)
Gọi D là điểm đối xứng của A qua I chỉ ra BHCD là hình bình hành. Khi đó M là trung điểm của HD, suy ra D(-5;-1).
I là trung điểm của AD, suy ra A(-1;7)
\(AI=\sqrt{20}\), phương trình đường tròn ngoại tiếp tam giác ABC là : \(\left(x+3\right)^2+\left(y-3\right)^2=20\)
Tọa độ điểm B, C là nghiệm của hệ phương trình :
\(\begin{cases}y-1=0\\\left(x+3\right)^2+\left(y-3\right)^2=20\end{cases}\)\(\Leftrightarrow\begin{cases}x=1\\y=1\end{cases}\) hoặc \(\begin{cases}x=-7\\y=1\end{cases}\)
Vậy ta có \(B\left(1;1\right),C\left(-7;1\right)\) hoặc \(B\left(-7;1\right),C\left(1;1\right)\)
Suy ra \(A\left(-1;7\right);B\left(1;1\right),C\left(-7;1\right)\)
hoặc\(A\left(-1;7\right);B\left(-7;1\right),C\left(1;1\right)\)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Nguyễn Đình Hữu
Trong mặt phẳng Oxy, cho 3 điểm A(1;3); B(-5;6); C(0;1)a) Chứng minh 3 điểm A, B, C tạo thành một tam giác. Tìm tọa độ trọng tâm G của tam giác ABCb) Tìm tọa độ điểm D sao cho ABCD là hình bình hànhc) Tìm tọa độ điểm H là chân đường cao kẻ từ A đến BC. Tính diện tích tam giác ABC
Xem chi tiết Lớp 10 Toán Chương 2: TÍCH VÔ HƯỚNG CỦA HAI VECTƠ VÀ ỨNG DỤNG 0 0 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A( 4;3); B (2;7) và C(– 3; -8). Tìm toạ độ chân đường cao A’ kẻ từ đỉnh A xuống cạnh BC
A. ( 1; -4)
B. (- 1; 4)
C. ( 1; 4)
D. (4; 1)
Xem chi tiết Lớp 10 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  9 tháng 7 2018 lúc 7:06
9 tháng 7 2018 lúc 7:06 
 Gửi Hủy
Gửi Hủy 
- Thu Hà Lê
-
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(-2;4), B(4;1), C(-2;-1). Tìm tọa độ trực tâm H tam giác.
Xem chi tiết Lớp 10 Toán Chương 3: PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG 1 0 Gửi Hủy
Gửi Hủy  Nguyễn Lê Phước Thịnh CTV
Nguyễn Lê Phước Thịnh CTV  16 tháng 2 2023 lúc 10:16
16 tháng 2 2023 lúc 10:16 vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1
Đúng 1 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Hoàng Tiến Thành
bài 1
câu 1.1: Cho 3 điểm A(4;3) B(2;7) C(-3;-8)
a. Viết phương trình đường cao từ đỉnh A của tam giác ABC. Tìm tọa độ trực tâm H của tam giác ABC
b. Viết phương trình đường tròn ngoại tiếp tam giác ABC
Câu 1.2: Trong mặt phẳng Oxy, cho điểm A(-1;4) B(3;2)
a. Viết phương trình tổng quát của đường thẳng AB
b. Viết phương trình đường tròn đường kính AB
Câu 2: Trong mặt phẳng Oxy, cho đường tròn (C): (x-3)2 + (y+2)2 = 16
a. Tìm tâm và bán kính của đường tròn (C)
b. Viết phương trình đường thẳng (d) tiếp xúc với đường tròn (C) biết d || △: 3x-4y+2= 0
mong mn giúp ạ
Xem chi tiết Lớp 10 Toán 4 0 Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  30 tháng 7 2021 lúc 0:22
30 tháng 7 2021 lúc 0:22 1.2
a.
\(\overrightarrow{AB}=\left(4;-2\right)=2\left(2;-1\right)\Rightarrow\) đường thẳng AB nhận (1;2) là 1 vtpt
Phương trình đường thẳng AB:
\(1\left(x+1\right)+2\left(y-4\right)=0\Leftrightarrow x+2y-7=0\)
b.
Gọi M là trung điểm AB \(\Rightarrow M\left(1;3\right)\)
\(AB=\sqrt{4^2+\left(-2\right)^2}=2\sqrt{5}\) \(\Rightarrow AM=\dfrac{1}{2}AB=\sqrt{5}\)
Đường tròn đường kính AB có tâm M và bán kính \(R=AM=\sqrt{5}\) nên có pt:
\(\left(x-1\right)^2+\left(y-3\right)^2=5\)
Đúng 1 Bình luận (0) Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  30 tháng 7 2021 lúc 0:12
30 tháng 7 2021 lúc 0:12 1.1
a. \(\overrightarrow{CB}=\left(5;15\right)=5\left(1;3\right)\) ; \(\overrightarrow{CA}=\left(7;11\right)\)
Đường cao qua A vuông góc BC nên nhận (1;3) là 1 vtpt
Phương trình đường cao đi qua A có dạng:
\(1\left(x-4\right)+3\left(y-3\right)=0\Leftrightarrow x+3y-13=0\)
Đường cao qua B vuông góc AC nhận (7;11) là 1 vtpt có dạng
\(7\left(x-2\right)+11\left(y-7\right)=0\Leftrightarrow7x+11y-91=0\)
Trực tâm H là giao điểm 2 đường cao nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+3y-13=0\\7x+11y-91=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=13\\y=0\end{matrix}\right.\)
\(\Rightarrow H\left(13;0\right)\)
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy  Nguyễn Việt Lâm CTV
Nguyễn Việt Lâm CTV  30 tháng 7 2021 lúc 0:19
30 tháng 7 2021 lúc 0:19 1.1
b.
Gọi tâm đường tròn ngoại tiếp là \(I\left(a;b\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AI}=\left(a-4;b-3\right)\\\overrightarrow{BI}=\left(a-2;b-7\right)\\\overrightarrow{CI}=\left(a+3;b+8\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}AI^2=\left(a-4\right)^2+\left(b-3\right)^2\\BI^2=\left(a-2\right)^2+\left(b-7\right)^2\\CI^2=\left(a+3\right)^2+\left(b+8\right)^2\end{matrix}\right.\)
Do I là tâm đường tròn nên: \(\left\{{}\begin{matrix}AI=BI\\AI=CI\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}AI^2=BI^2\\AI^2=CI^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(a-4\right)^2+\left(b-3\right)^2=\left(a-2\right)^2+\left(b-7\right)^2\\\left(a-4\right)^2+\left(b-3\right)^2=\left(a+3\right)^2+\left(b+8\right)^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-2b+7=0\\7a+11b+24=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-5\\b=1\end{matrix}\right.\)
\(\Rightarrow I\left(-5;1\right)\Rightarrow\overrightarrow{CI}=\left(-2;9\right)\Rightarrow R^2=CI^2=\left(-2\right)^2+9^2=85\)
Phương trình đường tròn:
\(\left(x+5\right)^2+\left(y-1\right)^2=85\)
Đúng 0 Bình luận (0) Gửi Hủy Xem thêm câu trả lời
Gửi Hủy Xem thêm câu trả lời 
- Tấn Đạt
Trong mặt phẳng tọa độ Oxy cho tam giác ABC có A(1;5) B(-4;-5) C(4;-1)
a) Tìm tọa độ chân đường phân giác trong và ngoài cho góc A
b) Tìm tọa độ tâm đường tròn nối tiếp tam giác ABC
Xem chi tiết Lớp 10 Toán §2. Phương trình đường tròn 0 0 Gửi Hủy
Gửi Hủy 
- Nguyễn Cường
Trong mặt phẳng tọa độ Oxy cho A(-2;2),B(6;6),C(2;-2). a) Tìm tọa độ trực tâm H của tam giác ABC; tọa độ tâm đường tròn ngoại tiếp I tam giác ABC; tọa độ trọng tâm G của tam giác ABC. b) Chứng minh : IH=-3IG. c) Gọi AD là đường kính của đường tròn ngoại tiếp tam giác ABC. Chứng minh tứ giác ABCD là hình bình hành.
mong mn giúp mình với ạ
Xem chi tiết Lớp 10 Toán 0 0 Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 1), B(4; 13), C(5; 0). Tọa độ trực tâm H của tam giác ABC là
A.(2; 2)
B. (1; 1)
C.( -2; -2)
D. (-1; -1)
Xem chi tiết Lớp 10 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  4 tháng 1 2017 lúc 9:39
4 tháng 1 2017 lúc 9:39 A B → = 3 ; 12 , A C → = 4 ; − 1 ⇒ ( A B ) ⃗ . ( A C ) ⃗ = 3 . 4 + 12 . ( - 1 ) = 0 ⇒ ∆ A B C vuông tại A. Trực tâm của tam giác là đỉnh A. Chọn B
Đúng 0 Bình luận (0) Gửi Hủy
Gửi Hủy 
- Pham Trong Bach
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có điểm M - 9 2 ; 3 2 là trung điểm của cạnh AB, điểm H(-2;4) và điểm I(-1;1) lần lượt là chân đường cao kẻ từ B và tâm đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ điểm C, biết A có tung độ âm.
A. C(-4;5)
B. C(-5;2)
C. C(4;1)
D. D(-1;6)
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy
Gửi Hủy  Cao Minh Tâm
Cao Minh Tâm  13 tháng 9 2019 lúc 11:11
13 tháng 9 2019 lúc 11:11 

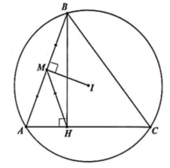
 Gửi Hủy
Gửi Hủy Từ khóa » Tìm Tọa độ điểm H Là Chân đường Cao
-
5) Và B(-2;8) Và C(6;9) Tìm Tọa độ điểm H Là Chân Của đường Cao Vẽ ...
-
Tìm Tọa độ Của điểm H, Biết H Là Chân đường Cao Kẻ Từ B(1;2)
-
3) : B(2;-1) Và C(-1; 5). Tính Tọa độ Chân đường Cao - Khóa Học
-
6).Gọi H Là Chân đường Cao Kẻ Từ A.Tìm Tọa độ điểm H? - MTrend
-
Tìm Tọa độ Chân đường Cao Hạ Từ đỉnh A Của Tam Giác ABC
-
Trong Mặt Phẳng Tọa độ (Oxy, ) Cho Tam Giác (ABC ) Có (A( (4;3
-
Tìm Tọa độ Chân đường Cao Của Tam Giác - Bùi Tuấn Anh - Học Để Thi
-
Top 10 Tìm Tọa độ Chân đường Cao Vẽ Từ A Và Trực Tam Của Tam Giác ...
-
Tính Tọa độ Chân đường Cao Của Tam Giác Kẻ Từ A Biết A(1;2 ), B(3
-
7 ); C(3;8). Tìm Toạ độ Chân đường Cao Kẻ Từ đỉnh A Xuống BC - Hoc24
-
Trong Mặt Phẳng Tọa độ Oxy, Cho Tam Giác ABC Có A(0;2), B