Ứng Dụng Vòng Tròn Lượng Giác Trong Các Bài Toán Về Dao động điều ...

ỨNG DỤNG VÒNG TRÒN LƯỢNG GIÁC TRONG CÁC BÀI TOÁN VỀ DAO ĐỘNG ĐIỀU HÒA

Mối quan hệ giữa chuyển động tròn đều và dao động điều hòa

Xét một điểm M chuyển động tròn đều trên đường tròn tâm O theo chiều dương với tốc độ góc ω. Gọi P là hình chiếu của M lên trục Ox.

Giả sử ban đầu (t = 0) điểm M ở vị trí Mo được xác định bằng góc φ. Ở thời điểm t, nó chuyển động đến M, xác định bởi góc:  φ + α với α = ωt.

Khi đó tọa độ của điểm P là:

x = \(\overline{OP}\) = OM.cos(ωt + φ)

Đặt OM = A, phương trình tọa độ của P được viết thành: x  = A.cos(ωt + φ).

Vậy điểm P dao động điều hòa.

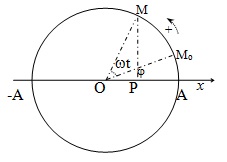
*Kết luận: Một dao động điều hòa có thể được coi như hình chiếu của một vật chuyển động tròn đều lên trục đi qua tâm nằm trong mặt phẳng quỹ đạo.

*Chú ý quan trọng: Khi vật dao động điều hoà chuyển động theo chiều dương thì chất điểm M ở dưới và ngược  lại

Ứng dụng đường tròn lượng giác  trong dao động điều hòa là một dạng bài toán khó. Để giải bài này bạn đọc phải nắm chắc kiến thức lượng giác. Bạn đọc hãy tham khảo bài giảng của thầy Phạm Quốc Toản để hiểu rõ hơn 

Bài toán 1: Tìm thời gian ngắn nhất vật đi từ A => B.

Ví dụ: Một vật dao động điều hòa với T. Hãy xác định thời gian ngắn nhất để vật đi từ vị trí cân bằng đến  \(\frac{A\sqrt{2}}{2}\)

Bài toán 2: Xác định thời điểm vật qua vị trí M cho trước

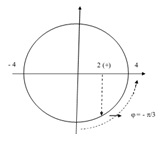
Ví dụ: Một vật dao động điều hòa với phương trình x = 4cos(6πt + π/3) cm.

a. Xác định thời điểm vật qua vị trí x = 2 cm theo chiều dương lần thứ 2 kể từ thời điểm ban đầu.

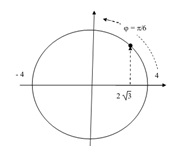
b.Thời điểm vật qua vị trí x = 2\(\sqrt{3}\)cm theo chiều âm lần 3 kể từ t = 2s.

Hướng dẫn:

a)- Vật qua vị trí x = 2cm (+):

=> 6πt + π/3  = -π/3 + k.2π

=>6πt = - 2π/3 + k.2π

=> t =  \(-\frac{1}{9}+\frac{k}{3}\geq 0\)=> k = (1, 2, 3…)

- Vậy vật đi qua lần thứ 2, ứng với k = 2.=> t = \(-\frac{1}{9}+\frac{2}{3}=\frac{5}{9}s\)

b.  Vật qua vị trí x = 2\(\sqrt{3}\)cm theo chiều âm:

=> 6πt + π/3  =π/6 + k.2π

=> 6πt = - π/6 + k.2π

=> t = - \(\frac{1}{36}+\frac{k}{3}\)

Vì t ≥ 2 => t = -  \(\frac{1}{36}+\frac{k}{3}\geq 2\) Vậy k = (7, 8, 9…)

- Vật đi qua lần thứ 3 ứng với k = 9

=> t = -\(\frac{1}{36}+\frac{k}{3}\)=\(\frac{1}{36}+\frac{9}{3}\)  = 2,97 s

Bài toán 3: Xác định quãng đường

Loại 1: Bài toán xác định quãng đường vật đi được trong khoảng thời gian ∆t.

Ví dụ: Vật dao động điều hòa theo phương trình x = 10cos(πt - π/2) cm. Xác định quãng đường vật đi được trong khoảng thời gian từ t1 = 1,5s đến t2 = 13/3s?

Loại 2: Bài toán xác định Smax ; Smin vật đi được trong khoảng thời gian t (t < \(\frac{T}{2}\))

Ví dụ: Vật dao động điều hòa với phương trình x = 5cos(4πt + π/6) cm. Tìm quãng đường lớn nhất vật đi được trong khoảng thời gian \(\frac{T}{6}\)

Loại 3: Tìm Smax ; Smin vật đi được trong khoảng thời gian t (T > t > \(\frac{T}{2}\) )

Ví dụ: Một vật dao động điều hòa với biên độ A. Tìm quãng đường nhỏ nhất vật đi được trong khoảng thời gian 2T/3.

Bài toán 4: Tính tốc độ trung bình

Ví dụ: Một vật dao động điều hòa theo phương trình x = 2cos(2πt + π/4) cm. Tính tốc độ trung bình của vật trong khoảng thời gian từ t1 = 2s đến t2 = 4,875s?

Bài toán 5: Xác định số lần vật qua vị trí x cho trước trong khoảng thời gian Dt

Ví dụ: Một vật dao động điều hòa với phương trình x = 6cos(4πt + \(\frac{\pi }{3}\)) cm. Trong một giây đầu tiên vật qua vị trí cân bằng bao nhiêu lần