TP2 : Approximation De π Par La Méthode D'Archimède

Nos manuelsSe connecterSommaireAccueil du manuelMathématiques Terminale SpécialitéTélécharger l'applicationLivre du professeurFermer le sommaireSommaireMes pagesAller à la pageN° PageOuverturep. 1-17AlgèbreRappelsp. 445-446

Rappels de première

Algèbre et géométrieCh. 1

Combinatoire et dénombrement

Ch. 2

Vecteurs, droites et plans de l’espace

Ch. 3

Orthogonalité et distances dans l’espace

AnalyseCh. 4

Suites

Ch. 5

Limites de fonctions

Ch. 6

Continuité

Ch. 7

Compléments sur la dérivation

Ch. 8

Logarithme népérien

Ch. 9

Fonctions trigonométriques

Ch. 10

Primitives - Équations différentielles

Ch. 11

Calcul intégral

ProbabilitésCh. 12

Loi binomiale

Ch. 13

Sommes de variables aléatoires

Ch. 14

Loi des grands nombres

Annexes

Exercices transversaux

Grand Oral

Apprendre à démontrer

Cahier d'algorithmique et de programmation

/ 451EditerTéléchargerPartagerVue papierDécouvrez la vue papier en cliquant iciPage précédente Chapitre 4TP INFO 2 Approximation de \pi par la méthode d'Archimède Ressource affichée de l'autre côté.Faites défiler pour voir la suite.Énoncé \pi est le périmètre d'un cercle \mathcal{C} de diamètre 1. Vers 250 av. J.‑C., pour déterminer une valeur approchée de ce nombre, Archimède décida de considérer des polygones réguliers ayant le même nombre de côtés, l'un étant inscrit dans le cercle \mathcal{C} (en bleu) et l'autre lui étant circonscrit (rouge). Pour tout n \geqslant 3, notons \text{S}_n le périmètre du polygone régulier à n côtés inscrit dans le cercle et \text{T}_n le périmètre du polygone régulier à n côtés circonscrit à ce cercle. On peut alors montrer (voir « Pour aller plus loin ») que pour tout n \geqslant 3, on a les relations suivantes : \mathrm{T}_{2 n}=\frac{2 \mathrm{S}_{n} \mathrm{T}_{n}}{\mathrm{S}_{n}+\mathrm{T}_{n}} et \mathrm{S}_{2 n}=\sqrt{\mathrm{S}_{n} \mathrm{T}_{2 n}}. Question préliminaire : Déterminer les valeurs de \text{T}_4 et \text{S}_4. Ressource affichée de l'autre côté.Faites défiler pour voir la suite.Objectif Déterminer un encadrement de \pi en utilisant une des deux méthodes. Ressource affichée de l'autre côté.Faites défiler pour voir la suite.

Méthode 1Tableur

1. Reproduire le tableau ci‑dessous. Quelles valeurs doit‑on entrer dans les cellules B2 et C2 ? (Fichier téléchargeable ici). 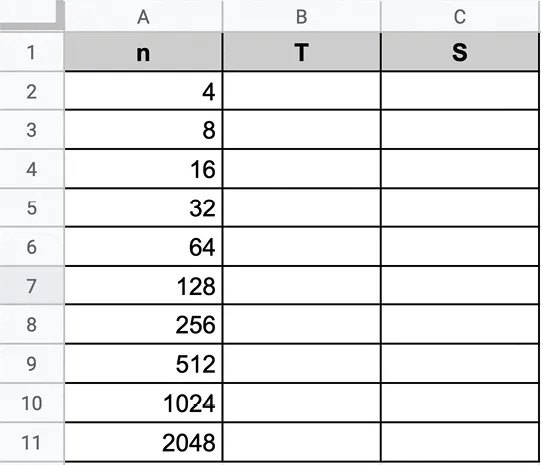2. Quelle formule doit‑on saisir dans la cellule B3 pour obtenir \text{T}_8 ? 3. Quelle formule doit‑on saisir dans la cellule C3 pour obtenir \text{S}_8 ? 4. Étirer les formules jusqu'à la ligne 11. Quel encadrement de \pi obtient‑on à ce stade ? Ressource affichée de l'autre côté.Faites défiler pour voir la suite.

Méthode 2Python

Voici un algorithme permettant de calculer les valeurs successives des suites \left(\mathrm{T}_{2^{n}}\right) et \left(\mathrm{S}_{2^{n}}\right). from math import * def archimede(n) : T = ... S = ... for k in range(n) : T = ... S = ... print("T =", T, "S =", S) 1. Compléter les lignes 4 et 5 de cet algorithme pour initialiser l'algorithme avec les valeurs \text{T}_4 et \text{S}_4. 2. Compléter les lignes 7 et 8 pour calculer les valeurs successives des suites \left(\mathrm{T}_{2^{n}}\right) et \left(\mathrm{S}_{2^{n}}\right). 3. Quelle valeur de n doit‑on entrer pour obtenir les valeurs des périmètres des polygones à 2 048 côtés inscrit dans le cercle et circonscrit à celui‑ci ? Quel encadrement de \pi obtient‑on alors ? Ressource affichée de l'autre côté.Faites défiler pour voir la suite.

Pour aller plus loin

1. Montrer que pour tout n\geqslant3, \mathrm{S}_{n}=n \sin \left(\frac{\pi}{n}\right) et \mathrm{T}_{n}=n \tan \left(\frac{\pi}{n}\right). 2. En utilisant la formule trigonométrique suivante : \cos (\theta)+1=2 \cos ^{2}\left(\frac{\theta}{2}\right), montrer que pour tout n\geqslant3, \frac{2 \mathrm{S}_{n} \mathrm{T}_{n}}{\mathrm{S}_{n}+\mathrm{T}_{n}}=2 n \frac{\sin \left(\frac{\pi}{n}\right)}{2 \cos ^{2}\left(\frac{\pi}{2 n}\right)}. 3. En utilisant la formule trigonométrique \sin (\theta)=2 \sin \left(\frac{\theta}{2}\right) \cos \left(\frac{\theta}{2}\right) : a. démontrer que, pour tout n\geqslant3, \sqrt{\mathrm{S}_{n} \mathrm{T}_{2 n}}=n \frac{\sin \left(\frac{\pi}{n}\right)}{\cos \left(\frac{\pi}{2 n}\right)}. b. démontrer que, pour tout n\geqslant3, \frac{2 \mathrm{S}_{n} \mathrm{T}_{n}}{\mathrm{S}_{n}+\mathrm{T}_{n}}=\mathrm{T}_{2 n} et \sqrt{\mathrm{S}_{n} \mathrm{T}_{2 n}}=\mathrm{S}_{2 n}. Page suivantePlein écranOptions d’affichage

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

Je contribue !

j'ai une idée !

Oups, une coquille