Bài 10: Tiệm Cận

A. Lý thuyết 1. Đường tiệm cận ngang a) y = b được gọi là tiệm cận ngang của đồ thị hàm số y = f(x) nếu thỏa mãn một trong các điều kiện sau

\(\lim_{x\rightarrow -\infty } f(x) = b\) \(\lim_{x\rightarrow +\infty } f(x) = b\) 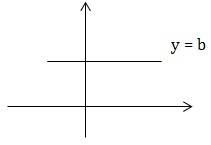b) Chú ý ĐK để đồ thị hàm số \(y = \frac{P(x)}{Q(x)}\) , P(x), Q(x) là các đa thức có tiệm cận ngang là bậc tử ≤ bậc mẫu. \(y = \frac{a_nx^n + ... + a_0}{b_mx^m + ... + b_0} \ \ \ m, n \in N; a_n\neq 0; b_m\neq 0\) ĐK có tiệm cận ngang n ≤ m Kết quả: n = m: tiệm cận ngang \(y = \frac{a_n}{b_m}\)

n < m: tiệm cận ngang y = 0

2. Đường tiệm cận đứng a) x = a được gọi là đường tiệm cận đứng của đồ thị hàm số y = f(x) nếu thỏa mãn một trong các điều kiện sau \(\lim_{x\rightarrow a^+} f(x) = \pm \infty\) \(\lim_{x\rightarrow a^-} f(x) = \pm \infty\)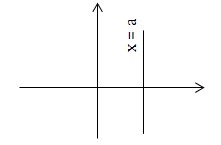

b) Chú ý

+) x = a là đường tiệm cận đứng của đồ thị y = f(x) thì a ∉ TXĐ f(x). +) Đối với hàm phân thức \(y = \frac{P(x)}{Q(x)}\) thì a là nghiệm Q(x) = 0.

B. Bài tập VD1: Tìm tiệm cận của đồ thị hàm số \(y=\frac{3x-1}{2x+5}\)

Giải: \(\lim_{x\rightarrow +\infty } y = \lim_{x\rightarrow +\infty } \frac{3x-1}{2x+5} = \lim_{x\rightarrow +\infty }\frac{3-\frac{1}{x}}{2+\frac{5}{x}} = \frac{3}{2}\) Vậy \(y = \frac{3}{2}\) là đường tiệm cận ngang. \(\lim_{x\rightarrow -\frac{5}{2}} y = -\infty\) Vậy \(x = -\frac{5}{2}\) là đường tiệm cận đứng của đồ thị hàm số. VD2: Tìm tiệm cận của đồ thị hàm số \(y = \frac{4x + 5}{3x - 1}\) Giải: \(\lim_{x \rightarrow -\infty } y = \lim_{x \rightarrow -\infty } \frac{4x + 5}{3x - 1} = \lim_{x \rightarrow -\infty } \frac{4 + \frac{5}{x}}{3-\frac{1}{x} }= \frac{4}{3}\) Vậy \(y = \frac{4}{3}\) là đường tiệm cận ngang. \(\lim_{x\rightarrow \frac{1}{3}^-} = - \infty\) Vậy \(y = \frac{1}{3}\) là đường tiệm cận đứng. VD3: Tìm tiệm cận ngang của đồ thị hàm số \(f(x) = \frac{2x + 9}{\sqrt{x^2 + 1} + 3x + 5}\) Giải: \(\lim_{x\rightarrow +\infty } f(x) = \lim_{x\rightarrow +\infty } \frac{2x + 9}{\sqrt{x^2 + 1} + 3x + 5}\) \(= \lim_{x\rightarrow +\infty } \frac{2 + \frac{9}{x}}{\sqrt{1+\frac{1}{x^2}} + 3 + \frac{5}{x}}\left ( \frac{\sqrt{x^2 + 1}}{x} = \frac{\sqrt{x^2 + 1}}{\sqrt{x^2}} (\ do\ x > 0)= \sqrt{1 + \frac{1}{x^2}} \right )\) \(=\frac{2}{4} = \frac{1}{2}\) Vậy \(y = \frac{1}{2}\) là tiệm cận ngang. \(\lim_{x\rightarrow -\infty } f(x) = \lim_{x\rightarrow -\infty } \frac{2x + 9}{\sqrt{x^2 + 1} + 3x + 5}\) \(= \lim_{x\rightarrow -\infty } \frac{2 + \frac{9}{x}}{-\sqrt{1 + \frac{1}{x^2}} + 3 + \frac{5}{x}}\) \(= \frac{2}{-1 + 3} = 1\) Vậy y = 1 là tiệm cận ngang.

VD4: Tìm m để đồ thị ham số \(y = \frac{(2m + 3)x + 5}{3x - 1}\) có tiệm cận ngang y = 2.

Giải: \(\lim_{x\rightarrow +\infty } y = \lim_{x\rightarrow +\infty } \frac{(2m + 3)x + 5}{3x - 1}\) \(\lim_{x\rightarrow +\infty } \frac{2m + 3 + \frac{5}{x}}{3 - \frac{1}{x}}\) \(= \frac{2m+3}{3}\) Vậy \(y= \frac{2m+3}{3}\) là tiệm cận ngang. y = 2 là đường tiệm cận ngang khi \(\frac{2m+3}{3} = 2\) ⇔ 2m + 3 = 6 ⇔ 2m = 3 \(\Leftrightarrow m = \frac{3}{2}\) VD5: Tìm m để đồ thị hàm số \(y = \frac{4x + 6}{(2m+1)x + 1}\) không có tiệm cận. Giải: TH1: \(2m + 1 = 0 \Leftrightarrow m = -\frac{1}{2}\) Khi đó y = 4x + 6 Vậy \(m = -\frac{1}{2}\) thỏa mãn TH2: 2m + 1 ≠ 0 \((2m + 1)x + 1 = 0 \Leftrightarrow x = -\frac{1}{2m+1}\) \(I=\lim_{x \rightarrow {-\frac{1}{2m+1}}^+} \frac{4x + 6}{(2m + 1)x + 1}\) \(I = \lim_{x \rightarrow {-\frac{1}{2m+1}}^+} (4x + 6) = 4.\left ( -\frac{1}{2m+1} \right ) + 6\) \(= \frac{-4 + 12m + 6}{2m + 1} = \frac{12m + 2}{2m + 1}\) 12m + 2 ≠ 0 thì \(I = \pm \infty\) 12m + 2 = 0 ⇔ \(m = - \frac{1}{6}\) thì \(y = \frac{4x + 6}{\left ( -\frac{1}{3} + 1 \right )x + 1} = 6\) \(m = - \frac{1}{6}\) (thỏa mãn) Vậy \(\left \{ -\frac{1}{2};-\frac{1}{6} \right \}\)