Tìm M để Hàm Số Có Tiệm Cận đứng - Giải Toán 12
Có thể bạn quan tâm
Cách tìm tiệm cận đứng của hàm số
- A. Định nghĩa tiệm cận đứng của đồ thị hàm số
- B. Cách tìm m để hàm số có tiệm cận đứng
- C. Công thức tính tiệm cận đứng của hàm phân thức dạng
- D. Bài tập tìm m để hàm số có tiệm cận đứng
- E. Bài tập tự rèn luyện tìm m để hàm số có tiệm cận đứng
- F. Đáp án bài tập tự rèn luyện
Tìm m để hàm số có tiệm cận đứng là một trong những kiến thức quan trọng trong chuyên đề Toán 12 Đường tiệm cận. Việc hiểu và vận dụng đúng cách lý thuyết tiệm cận đứng giúp học sinh không chỉ đạt kết quả tốt trong các kỳ thi mà còn có cái nhìn sâu sắc hơn về sự thay đổi của hàm số và các đặc điểm hình học liên quan. Trong bài viết này, chúng ta sẽ cùng nhau giải quyết bài toán tìm m để hàm số có tiệm cận đứng, qua đó làm rõ phương pháp giải bài tập tiệm cận đứng, cũng như các lưu ý quan trọng để tránh những sai sót khi làm bài. Hãy cùng khám phá!
- 300 câu hỏi trắc nghiệm môn Toán lớp 12 (Có đáp án)
- Bài tập trắc nghiệm cực trị của hàm số và điểm uốn (Có đáp án)
- Bài tập trắc nghiệm tính đơn điệu của hàm số
- Câu hỏi trắc nghiệm môn Toán lớp 12: Cực trị của hàm số
Tìm tham số m để hàm số có tiệm cận đứng
Bản quyền thuộc về VnDoc.Nghiêm cấm mọi hình thức sao chép nhằm mục đích thương mại.
A. Định nghĩa tiệm cận đứng của đồ thị hàm số
Cho đồ thị hàm số ![]() có tập xác định D.
có tập xác định D.
Nếu ![]() hoặc
hoặc ![]() thì đường thẳng
thì đường thẳng ![]() là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.
Chú ý. Đường thẳng x = x0 là đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
![]()
B. Cách tìm m để hàm số có tiệm cận đứng
Cho hàm số ![]() có tập xác định D:
có tập xác định D:
Bước 1. Muốn xác định đồ thị hàm số có tiệm cận hay không ta tìm nghiệm của phương trình v = 0. Ví dụ x = a là nghiệm của phương trình.
Bước 2. Xét x = a có là nghiệm của tử thức u:
+ Nếu x = a là không nghiệm của u = 0 thì x = a là một tiệm cận đứng.
+ Nếu x = a là nghiệm của u = 0 thì phân tích đa thức thành nhân tử:
 .
.
Rút gọn x – a:
- Nếu còn nhân tử x – a dưới mẫu thì x = a là một tiệm cận đứng của đồ thị hàm số.
- Nếu không còn nhân tử x – a trên tử hay ca tử và mẫu thì x – a không là tiệm cận đứng của đồ thị.
C. Công thức tính tiệm cận đứng của hàm phân thức dạng
Điều kiện để hàm phân thức ![]() có tiệm cận đứng là:
có tiệm cận đứng là: ![]() .
.
Chú ý:
- Hàm số ![]() có:
có:
- Tiệm cận ngang là:

- Tiệm cận đứng là:

- Hàm số ![]() có:
có:
- Tiệm cận đứng là:

- Tiệm cận ngang là:

- Hàm số hữu tỉ: ![]() không chia hết có đường tiệm cận xiên khi bậc của tử lớn hơn bậc của mẫu một bậc.
không chia hết có đường tiệm cận xiên khi bậc của tử lớn hơn bậc của mẫu một bậc.
D. Bài tập tìm m để hàm số có tiệm cận đứng
Bài tập 1: Tìm tất cả giá trị tham số m sao cho đồ thị hàm số ![]() có tiệm cận đứng?
có tiệm cận đứng?
Hướng dẫn giải
Mẫu có nghiệm ![]()
Để đồ thị hàm số có tiệm cận đứng thì: 
Vậy để đồ thị hàm số có tiệm cận đứng thì các giá trị m thỏa mãn là: ![]() .
.
Đáp án D
Bài tập 2: Cho đồ thị hàm số ![]() . Tìm tất cả các giá trị thực của m sao cho đồ thị hàm số có 2 tiệm cận đứng.
. Tìm tất cả các giá trị thực của m sao cho đồ thị hàm số có 2 tiệm cận đứng.
| A. | B. |
| C. | D. |
Hướng dẫn giải
Để hai đường thẳng x = 2 và x = 1 là tiệm cận đứng của đồ thị hàm số thì x = 1 và x = 2 không là nghiệm của ![]()

Vậy các giá trị tham số m thỏa mãn để đồ thị hàm số có 2 tiệm cận đứng là: ![]() .
.
Đáp án B
Bài tập 3: Cho đồ thị hàm số ![]() . Tìm tất cả giá trị tham số m để đồ thị hàm số không có tiệm cận đứng.
. Tìm tất cả giá trị tham số m để đồ thị hàm số không có tiệm cận đứng.
| A. | B. |
| C. | D. |
Hướng dẫn giải
Đồ thị hàm số không có tiệm cận đứng thì x = m là nghiệm của ![]()
![]()
![]()
![]()
![]()
Vậy tất cả các giá trị tham số m để đồ thị hàm số không có tiệm cận đứng là: ![]() .
.
Đáp án D
Bài tập 4: Tìm tất cả giá trị tham số m sao cho đồ thị hàm số ![]() có đúng một tiệm cận đứng.
có đúng một tiệm cận đứng.
| A. | B. |
| C. | D. |
Hướng dẫn giải
Ta có:
![]()
Để đồ thị hàm số có một tiệm cận đứng khi và chỉ khi:

Vậy các giá trị của tham số m sao cho đồ thị hàm số đã cho có đúng một tiệm cận đứng là ![]()
Đáp án A.
Bài tập 5. Có bao nhiêu giá trị nguyên của tham số thực ![]() thuộc đoạn
thuộc đoạn ![]() để hàm số
để hàm số ![]() có hai tiệm cận đứng.
có hai tiệm cận đứng.
Hướng dẫn giải
Để hàm số ![]() có hai tiệm cận đứng
có hai tiệm cận đứng ![]() có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác ![]()

![]()
Mà ![]()
![]() .
.
Vậy có tất cả ![]() giá trị nguyên thỏa mãn.
giá trị nguyên thỏa mãn.
E. Bài tập tự rèn luyện tìm m để hàm số có tiệm cận đứng
Câu 1: Tập hợp tất cả các giá trị thực của tham số ![]() để đồ thị hàm số
để đồ thị hàm số ![]() có đúng hai tiệm cận đứng?
có đúng hai tiệm cận đứng?
Câu 2. Có bao nhiêu giá trị nguyên của tham số ![]() để đồ thị hàm số
để đồ thị hàm số ![]() có đúng một tiệm cận đứng?
có đúng một tiệm cận đứng?
Câu 3: Tìm giá trị thực của tham số ![]() để đồ thị hàm sô
để đồ thị hàm sô![]() có đường tiệm cận đứng đi qua điểm
có đường tiệm cận đứng đi qua điểm ![]()
Câu 4: Tìm tất cả các giá trị thực của tham số ![]() để đồ thị hàm số
để đồ thị hàm số ![]() không có tiệm cận đứng.
không có tiệm cận đứng.
Câu 5. Tìm tất cả các giá trị thực của tham số ![]() để đồ thị hàm số
để đồ thị hàm số ![]() có đúng một tiệm cận đứng.
có đúng một tiệm cận đứng.
Câu 6. Tìm tất cả các giá trị thực của tham số ![]() để đồ thị hàm số
để đồ thị hàm số ![]() có đúng một tiệm cận ngang và đúng một tiệm cận đứng.
có đúng một tiệm cận ngang và đúng một tiệm cận đứng.
Câu 7. Tìm tất cả các giá trị của tham số ![]() để đồ thị hàm số
để đồ thị hàm số ![]() có tiệm cận ngang mà không có tiệm cận đứng.
có tiệm cận ngang mà không có tiệm cận đứng.
Câu 8. Có bao nhiêu giá trị nguyên của tham số thực ![]() thuộc đoạn
thuộc đoạn ![]() để hàm số
để hàm số ![]() có hai tiệm cận đứng.
có hai tiệm cận đứng.
Câu 9. Tìm trên đồ thị hàm số ![]() những điểm
những điểm ![]() sao cho khoảng cách từ
sao cho khoảng cách từ ![]() đến tiệm cận đứng bằng ba lần khoảng cách từ
đến tiệm cận đứng bằng ba lần khoảng cách từ ![]() đến tiệm cận ngang của đồ thị.
đến tiệm cận ngang của đồ thị.
Câu 10. Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
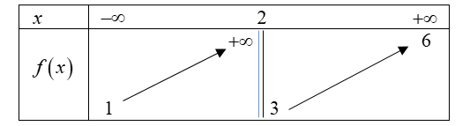
Hỏi có bao nhiêu giá trị nguyên của ![]() để đồ thị hàm số
để đồ thị hàm số  có đúng 3 tiệm cận đứng.
có đúng 3 tiệm cận đứng.
A. 1 B. 2 C. 3 D. 4
Câu 11. Cho hàm số ![]() có bảng biến thiên như sau:
có bảng biến thiên như sau:
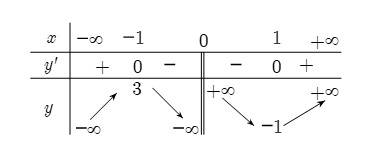
Có bao nhiêu số nguyên ![]() thuộc khoảng
thuộc khoảng ![]() để đồ thị hàm số
để đồ thị hàm số  có đúng đường tiệm cận?
có đúng đường tiệm cận?
A. 15 B. 6 C. 7 D. 14
F. Đáp án bài tập tự rèn luyện
Câu 1:
Điều kiện xác định ![]()
Vì ![]() nên để đồ thị hàm số có đúng hai tiệm cận đứng thì phương trình
nên để đồ thị hàm số có đúng hai tiệm cận đứng thì phương trình ![]() phải có hai nghiệm phân biệt lớn hơn
phải có hai nghiệm phân biệt lớn hơn ![]() .
.
Xét hàm số ![]() trên
trên ![]() có:
có:

Bảng biến thiên
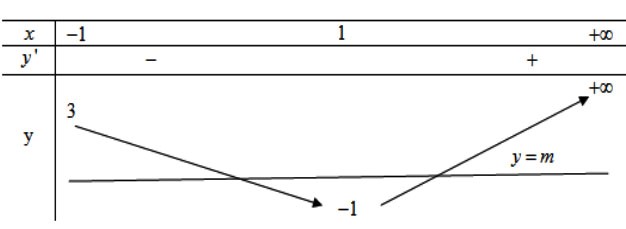
Phương trình (*) có hai nghiệm phân biệt lớn hơn ![]() khi
khi ![]() .
.
Vậy đáp án cần tìm là ![]() .
.
Câu 2
Đồ thị hàm số ![]() có đúng một tiệm cận đứng khi và chỉ khi phương trình
có đúng một tiệm cận đứng khi và chỉ khi phương trình ![]() có đúng một nghiệm
có đúng một nghiệm ![]()
Ta có: ![]()
Xét hàm số ![]() ta có:
ta có: 
Ta có bảng biến thiên như sau:
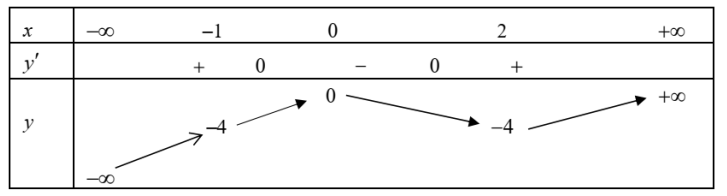
Từ bảng biến thiên suy ra ![]()
Mà ![]() nên
nên ![]()
Vậy có tất cả 6 giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Câu 3
TXĐ: ![]() .
.
Ta có  là tiệm cận đứng.
là tiệm cận đứng.
Do đó yêu cầu bài toán ![]() .
.
Câu 4
TXĐ: ![]() .
.
Ta có ![]()
![]()
Để đồ thị hàm số không có tiệm cận đứng thì các giới hạn ![]() tồn tại hữu hạn
tồn tại hữu hạn ![]()
Cách 2. (Chỉ áp dụng cho mẫu thức là bậc nhất)
Từ yêu cầu bài toán suy ra phương trình ![]() có một nghiệm là
có một nghiệm là ![]()
![]()
![]() .
.
Câu 5:
Để đồ thị hàm số ![]() có đúng một tiệm cận đứng
có đúng một tiệm cận đứng ![]() có nghiệm duy nhất
có nghiệm duy nhất
 .
.
Vậy có hai điểm thỏa mãn khoảng cách từ M đến tiệm cận đứng bằng ba lần khoảng cách từ M đến tiệm cận ngang của đồ thị hàm số.
Câu 6:
Ta có ![]() là tiệm cận ngang với mọi
là tiệm cận ngang với mọi ![]()
Để đồ thị hàm số ![]() có đúng một tiệm cận ngang và đúng một tiệm cận đứng
có đúng một tiệm cận ngang và đúng một tiệm cận đứng ![]()
Phương trình ![]() có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng
có nghiệm kép hoặc có hai nghiệm phân biệt trong đó có một nghiệm bằng ![]()
 .
.
Vậy có 2 giá trị thực của tham số m để đồ thị hàm số có đúng một tiệm cận ngang và đúng một tiệm cận đứng.
Câu 7.
Ta có ![]() là tiệm cận ngang với mọi m.
là tiệm cận ngang với mọi m.
Do đó để đồ thị hàm số có tiệm cận ngang mà không có tiệm cận đứng thì phương trình ![]() vô nghiệm
vô nghiệm ![]() .
.
Nhận xét. Bạn đọc dễ nhầm lẫn mà xét thêm trường hợp mẫu thức ![]() có nghiệm
có nghiệm ![]() . Điều này là sai, vì với
. Điều này là sai, vì với ![]() thì hàm số trở thành
thì hàm số trở thành ![]() . Đồ thị này vẫn còn tiệm cận đứng là
. Đồ thị này vẫn còn tiệm cận đứng là ![]() .
.
Câu 8.
Để hàm số  có hai tiệm cận đứng
có hai tiệm cận đứng ![]() có hai nghiệm phân biệt khác
có hai nghiệm phân biệt khác ![]()

![]()
Mà ![]()
![]() .
.
Vậy có tất cả giá trị nguyên thỏa mãn.
Câu 9.
Gọi ![]() với
với ![]() là điểm thuộc đồ thị.
là điểm thuộc đồ thị.
Đường tiệm cận đứng ![]() đường tiệm cận ngang
đường tiệm cận ngang ![]() .
.
Yêu cầu bài toán:
![]()
![]()
![]() .
.
Áp dụng công thức giải nhanh 
![]()
với ![]() .
.
Suy ra ![]() .
.
Tài liệu quá dài để hiển thị hết — hãy nhấn Tải về để xem trọn bộ!
--------------------------------------------------------------------
Trên đây là những hướng dẫn chi tiết về cách tìm m để hàm số có tiệm cận đứng trong chương trình Toán 12 Đường tiệm cận. Hy vọng rằng qua bài viết này, bạn đã nắm vững được phương pháp giải quyết các bài toán tiệm cận đứng một cách hiệu quả và chính xác. Để tiếp tục nâng cao kỹ năng Toán học, bạn có thể tham khảo thêm các bài viết khác về tiệm cận ngang, tiệm cận xiên, và các bài toán khác trong chương trình Toán 12. Đừng quên chia sẻ bài viết này với bạn bè và học sinh khác để cùng nhau nâng cao kiến thức và thành tích học tập. Chúc bạn học tốt và đạt kết quả cao trong kỳ thi sắp tới!
Mời bạn đọc tham khảo thêm một số tài liệu liên quan:
- 45 câu hỏi trắc nghiệm có đáp án môn Toán lớp 12: Tính đơn điệu của hàm số
- Câu hỏi trắc nghiệm môn Toán lớp 12: Tiếp tuyến của đồ thị hàm số
- 100 bài tập trắc nghiệm chuyên đề hàm số có đáp án
- Trắc nghiệm Toán 12 chương 1: Sự đồng biến, nghịch biến của hàm số
- Chuyên đề: Xác định tính đơn điệu của hàm số dựa vào đồ thị hàm số
- Bài toán Thực tế tối ưu diện tích và thể tích (Có lời giải chi tiết)
Từ khóa » Hàm Số Có Tiệm Cận đứng Khi Nào
-
Tìm M để Hàm Số Có Tiệm Cận đứng - Ôn Tập Toán 12
-
Tìm M để Hàm Số Có Tiệm Cận Ngang Tiệm Cận đứng - Toán Thầy Định
-
Tiệm Cận đứng Của đồ Thị Hàm Số - Toán Thầy Định
-
Lý Thuyết đường Tiệm Cận Của đồ Thị Hàm Số Và Luyện Tập Toán 12
-
Bài Tập Tìm M để Hàm Số Có Tiệm Cận đứng, Tiệm Cận Ngang Có đáp án
-
Cách Tìm Tiệm Cận đứng Và Tiệm Cận Ngang Của Hàm Số
-
Cách Tìm Tiệm Cận đứng Của đồ Thị Hàm Số Chính Xác 100%
-
Đường Tiệm Cận Của Hàm Số: Lý Thuyết & Bài Tập (Kèm Tài Liệu)
-
Đường Tiệm Cận Của đồ Thị Hàm Số, Trắc Nghiệm Toán Học Lớp 12
-
Tiệm Cận Đứng Là Gì? Cách Tìm Tiệm Cận Đứng Của Đồ Thị Hàm Số
-
Tìm điều Kiện Của Tham Số M để đồ Thị Hàm Số Có Tiệm Cận đứng ...
-
Tìm điều Kiện Của Tham Số M để đồ Thị Hàm Số Có 1, 2, 3 Tiệm Cận ...
-
Bài Tập Tìm M để Hàm Số Có Tiệm Cận đứng - Tự Học 365
-
Bài 10: Tiệm Cận