Bài 3.15 (Sách Bài Tập Trang 103)Trong Không Gian Oxyz ... - Hoc24
HOC24
Lớp học Học bài Hỏi bài Giải bài tập Đề thi ĐGNL Tin tức Cuộc thi vui Khen thưởng- Tìm kiếm câu trả lời Tìm kiếm câu trả lời cho câu hỏi của bạn
Lớp học
- Lớp 12
- Lớp 11
- Lớp 10
- Lớp 9
- Lớp 8
- Lớp 7
- Lớp 6
- Lớp 5
- Lớp 4
- Lớp 3
- Lớp 2
- Lớp 1
Môn học
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Đạo đức
- Tự nhiên và xã hội
- Khoa học
- Lịch sử và Địa lý
- Tiếng việt
- Khoa học tự nhiên
- Hoạt động trải nghiệm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Chủ đề / Chương
Bài học
HOC24
Khách vãng lai Đăng nhập Đăng ký Khám phá Hỏi đáp Đề thi Tin tức Cuộc thi vui Khen thưởng - Tất cả
- Toán
- Vật lý
- Hóa học
- Sinh học
- Ngữ văn
- Tiếng anh
- Lịch sử
- Địa lý
- Tin học
- Công nghệ
- Giáo dục công dân
- Tiếng anh thí điểm
- Hoạt động trải nghiệm, hướng nghiệp
- Giáo dục kinh tế và pháp luật
Câu hỏi
Hủy Xác nhận phù hợp Chọn lớp Tất cả Lớp 12 Lớp 11 Lớp 10 Lớp 9 Lớp 8 Lớp 7 Lớp 6 Lớp 5 Lớp 4 Lớp 3 Lớp 2 Lớp 1 Môn học Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Tiếng anh thí điểm Đạo đức Tự nhiên và xã hội Khoa học Lịch sử và Địa lý Tiếng việt Khoa học tự nhiên Hoạt động trải nghiệm Hoạt động trải nghiệm, hướng nghiệp Giáo dục kinh tế và pháp luật Mới nhất Mới nhất Chưa trả lời Câu hỏi hay
- Bài 3.15
Trong không gian Oxyz hãy xác định tâm và bán kính các mặt cầu có phương trình sau đây :
a) \(x^2+y^2+z^2-6x+2y-16z-26=0\)
b) \(2x^2+2y^2+2z^2+8x-4y-12z-100=0\)
Xem chi tiết Lớp 12 Toán Bài 1: Hệ tọa độ trong không gian 1 0
Gửi Hủy 
Nguyen Thuy Hoa 
26 tháng 5 2017 lúc 16:43 a) Tâm \(I\left(3;-1;8\right)\), bán kính \(r=10\)
b) Tâm \(I\left(-2;1;3\right)\), bán kính \(r=8\)
Đúng 0 Bình luận (0) Gửi Hủy - Bài 5
Trong không gian Oxyz, tìm tâm và bán kính các mặt cầu có phương trình dưới đây ?
a) \(x^2+y^2+z^2-8x-2y+1=0\)
b) \(3x^2+3y^2+3z^2-6x+8y+15z-3=0\)
Xem chi tiết Lớp 12 Toán Bài 1: Hệ tọa độ trong không gian 1 0 Gửi Hủy 
Hai Binh 27 tháng 4 2017 lúc 17:28 
Gửi Hủy 
- Pham Trong Bach
Trong không gian với hệ trục tọa độ Oxyz cho mặt cầu S : x 2 + y 2 + z 2 - 6 x - 4 y - 12 z = 0 và mặt phẳng P : 2 x + y - z - 2 = 0 . Tính diện tích thiết diện của mặt cầu (S) cắt bởi mặt phẳng (P).
A. S = 49 π
B. S = 50 π
C. S = 25 π
D. S = 36 π
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy 
Cao Minh Tâm 
30 tháng 7 2017 lúc 11:52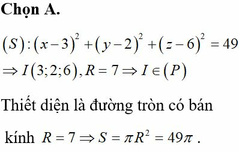 
Gửi Hủy - Pham Trong Bach
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình
x 2 + y 2 + z 2 − 2 x + 4 y − 6 z − 2 = 0
Xác định tâm I và bán kính mặt cầu.
A. I 1 ; 2 ; 3 , R = 4.
B. I 1 ; - 2 ; 3 , R = 4.
C. I 2 ; − 4 ; 6 , R = 16.
D. I - 2 ; 4 ; 6 , R = 16.
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy Cao Minh Tâm 23 tháng 7 2017 lúc 7:06 Đáp án B.
x 2 + y 2 + z 2 − 2 x + 4 y − 6 z − 2 = 0 ⇔ x − 1 2 + y + 2 2 + z − 3 2 = 1 + 4 + 9 + 2 = 16 ⇒ I 1 ; − 2 ; 3 , R = 4.
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Hãy cho biết phương trình nào trong các phương trình sau đây là phương trình đường tròn:
2x2 + y2 – 8x + 2y – 1 = 0;
x2 + y2 + 2x – 4y – 4 = 0;
x2 + y2 – 2x – 6y + 20 = 0;
x2 + y2 + 6x + 2y + 10 = 0.
Xem chi tiết Lớp 10 Toán 1 0 Gửi Hủy Cao Minh Tâm 9 tháng 9 2017 lúc 5:32 + 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 2x + 4y + 2z - 19 = 0 và mặt phẳng (P): x - 2y + 2z - 12 = 0. Tìm tọa độ tâm và bán kính của đường tròn đó.
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy Cao Minh Tâm 27 tháng 3 2017 lúc 11:09 Gọi d là đường thẳng qua I và vuông góc với (P). Phương trình của d là
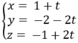
Tâm của (C) là điểm H = d ∩ (P). Để tìm H ta thay phương trình của d vào phương trình của (P).
Ta có: 1 + t - 2(-2 - 2t) + 2(-1 + 2t) - 12 = 0
Suy ra t = 1, do đó H = (2; -4; 1).
Bán kính của (C) bằng
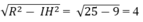
Gửi Hủy - Pham Trong Bach
Trong không gian Oxyz, cho mặt cầu ( S ) : x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 5 = 0 Phương trình mặt phẳng (Q) chứa trục Ox và cắt (S) theo giao tuyến là một đường tròn bán kính bằng 2 là
A. (Q): 2y+z=0
B. (Q): 2x-z=0
C. (Q): y-2z=0
D. (Q): 2y-z=0
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy Cao Minh Tâm 10 tháng 8 2017 lúc 17:05 Đáp án D
Phương pháp:
Trong đó
d: khoảng cách từ tâm O đến mặt phẳng (P),
r: bán kính đường tròn là giao tuyến của mặt cầu (S) và mặt phẳng (P)
R: bán kính hình cầu.
Cách giải:
( S ) : x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 5 = 0
=> (S) có tâm I(3;-2;1) bán kính R = 3
(Q) cắt (S) theo giao tuyến là một đường tròn bán kính r = 2
Ta có
là một VTCP (Q)
Khi đó
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT n → =(0;b;c) là:
Khoảng cách từ tâm I đến (Q):
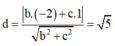
Phương trình mặt phẳng (Q): 2y -z =0
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Trong không gian Oxyz, cho mặt cầu (S): x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 5 = 0 . Phương trình mặt phẳng (Q) chứa trục Ox và cắt (S) theo giao tuyến là một đường tròn bán kính bằng 2 là
A. (Q): 2y + z = 0
B. (Q): 2x - z = 0
C. (Q): y - 2z = 0
D. (Q): 2y - z = 0
Xem chi tiết Lớp 0 Toán 1 0 Gửi Hủy Cao Minh Tâm 30 tháng 6 2019 lúc 7:44 Đáp án D
Phương pháp: d 2 + r 2 = R 2
Trong đó,
d: khoảng cách từ tâm O đến mặt phẳng (P),
r: bán kính đường tròn là giao tuyến của mặt cầu (S)
và mặt phẳng (P),
R: bán kính hình cầu.
Cách giải:
(S): x 2 + y 2 + z 2 - 6 x + 4 y - 2 z + 5 = 0 <=> x - 3 2 + y + 2 2 + z - 1 2 = 9
=> (S) có tâm I(3; –2;1) bán kính R = 3
(Q) cắt (S) theo giao tuyến là một đường tròn bán kính r = 2
Ta có: d 2 + r 2 = R 2 
Gọi n → a ; b ; c , n → ≠ 0 là một VTPT của (Q). Khi đó n → vuông góc với VTCP n → 1 ; 0 ; 0 của Ox
=>1.a + 0.b +).c = 0 ó a = 0
Phương trình mặt phẳng (Q) đi qua O(0;0;0) và có VTPT n → 0 ; b ; c , n → ≠ 0 là:
0.(x – 0) + b(y – 0) + c(z – 0) ó by + cz = 0
Khoảng cách từ tâm I đến (Q):
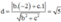
Cho c = –1 => b = 2 => n → 0 ; 2 ; - 1
Phương trình mặt phẳng (Q): 2y - z = 0
Đúng 0 Bình luận (0) Gửi Hủy - Pham Trong Bach
Trong không gian tọa độ Oxyz, cho mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 và mặt phẳng (P): x + 2y - 2z - 2 = 0. Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính là:
A. r = 6
B. r = 2 2
C. r = 4
D. r = 2 3
Xem chi tiết Lớp 12 Toán 1 0 Gửi Hủy Cao Minh Tâm 25 tháng 9 2018 lúc 7:15 Chọn C
Mặt cầu (S): x2 + y2 + z2 - 2x + 4y - 4z -16 = 0 có tâm I (1; -2; 2) bán kính R = 5
Khoảng cách từ I (1; -2; 2) đến mặt phẳng (P): x + 2y - 2z - 2 = 0 là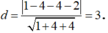 
Mặt phẳng cắt mặt cầu theo giao tuyến là một đường tròn có bán kính là: 
Gửi Hủy - Pham Trong Bach
Trong không gian với hệ tọa độ Oxyz, viết phương trình mặt phẳng tiếp xúc với (S): x 2 + y 2 + z 2 - 2 z - 4 y - 6 z - 2 = 0 và song song với (α): 4x + 3y - 12z+10 = 0
A.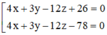 
B.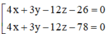 
C.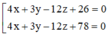 
D.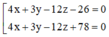 
Gửi Hủy Cao Minh Tâm 8 tháng 12 2018 lúc 8:10 Đáp án D
Phương pháp:
(P) // (α) => Phương trình mặt phẳng (P) có dạng 4x + 3y - 12z + D = 0 (D ≠ 0)
(P) tiếp xúc với (S) => d(I;(P)) = R với I; R là tâm và bán kính mặt cầu (S)
Cách giải:
Gọi mặt phẳng (P) là mặt phẳng cần tìm
(P) // (α) Phương trình mặt phẳng (P) có dạng 4x + 3y - 12z + D = 0 (D ≠ 0)
Mặt cầu (S) có tâm I (1;2;3), bán kính R = 4
(P) tiếp xúc với (S) => d(I;(P)) = R
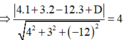
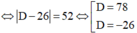
Vậy mặt phẳng (P) thỏa mãn yêu cầu bài toán có phương trình
Gửi Hủy Từ khóa » (s) X2+y2+z2−2x+2y−4z−2=0 ( S ) X 2 + Y 2 + Z 2 − 2 X + 2 Y − 4 Z − 2 = 0 Có Bán Kính Bằng
-
X^2+y^2+z^2−2y+4z−2=0. Bán Kính Của Mặt Cầu đã Cho Bằng
-
Trong Khôn Gian Oxyz, Cho Mặt Cầu: (S): X^2 +y^2 +z^2 -2x +2y -4z
-
Trong Không Gian Oxyz, Cho Mặt Cầu (S): X^2 + Y^2 + Z^2 - 2y + 4z -2=0
-
Trong Không Gian Oxyz, Cho Mặt Cầu ( S ):x^2 + Y^2 + Z^2 + 2y - 2z - 7
-
Trong Không Gian Oxyz Cho Mặt Cầu ( S ):x^2 + Y^2 + Z^2 - 2x + 2y
-
Trong Không Gian Oxyz, Cho Mặt Cầu (S) Có Phương Trình \({x^2} + {y ...
-
Cho Phương Trình: \({x^2} + {y^2} + {z^2} + 2x\cos \alpha
-
Trong Không Gian Oxyz , Cho Mặt Cầu (S):x2+y2+z2−4x+2y+2z−10 ...
-
Trong Không Gian Với Hệ Trục Tọa độ Oxyz, Cho Mặt Cầu (S): X2+y2+ ...
-
X2+y2+z2−2x−4y−6z−2=0 Và Mặt Phẳng (α):4x+3y−12z+10=0 ...
-
Consider The Equation Below. X2 − Y2 + Z2 - 2x + 2y + - Chegg
-
Trong Không Gian Với Hệ Tọa độ Oxyz, Tìm Tất Cả Các Giá Trị Của M
-
[PDF] HƯỚNG DẪN GIẢI BÀI TẬP HỌC PHẦN GIẢI TÍCH 2
-
Trong Không Gian Oxyz, Cho Mặt Cầu Mặt Phẳng = 0. Giá Trị Của M để ...
-
[PDF] Completing Squares In The Equation X2 + Y2 + Z2 + 4x - 2y - WebAssign
-
Trong Không Gian Tọa độ $Oxyz$ Cho Mặt Cầu $\left( S \right)$ Có ...
-
Trong Không Gian Oxyz, Cho Mặt Cầu ((S):{x^2} + {y^2} + {z^2} – 2x + 4y
-
Mặt Phẳng (Oyz) Cắt Mặt Cầu (S): X^2 +y^2 +z^2 +2x - Vietjack.online
-
Hình Học 12: Cho Mặt Phẳng (P): 2x – 3y + 4z – 5 = 0 Và Mặt Cầu (S)