Bài 4. Phân Tích Tương Quan Pearson R (Pearson's Correlation R)
Có thể bạn quan tâm
Phân tích tương quan Pearson r (cung cấp một hệ số tương quan Pearson, được ký hiệu là r) là thước đo độ mạnh của mối liên kết tuyến tính giữa hai biến. Về cơ bản, sự tương quan Pearson cố gắng vẽ một đường phù hợp nhất thông qua dữ liệu của hai biến và hệ số tương quan Pearson, r, cho biết khoảng cách tất cả các điểm dữ liệu này đến đường phù hợp nhất này (tức là các điểm dữ liệu này tốt như thế nào với mô hình / đường mới phù hợp nhất).
1. Khi nào sử dụng?
Phân tích tương quan Pearson, r, có thể được sử dụng làm ước lượng mẫu cho tương quan dân số, ρ (rho). Nó là một chỉ số không có thứ nguyên về mối quan hệ tuyến tính giữa hai biến ngẫu nhiên, giá trị bằng 0 có nghĩa là không có mối quan hệ tuyến tính giữa các biến và giá trị bằng 1 cho thấy mối quan hệ tuyến tính hoàn hảo. Nếu mối tương quan là âm, có nghĩa là giá trị tăng trên một biến được kết hợp với giá trị giảng trên biến kia. Giá trị của r có thể thay đổi giữa −1 và +1 bất kể kích thước đo lường của hai biến.
Tương quan Pearson, r, nên được coi là một thống kê mô tả (descriptive statistic) khi một nhà nghiên cứu muốn định lượng mức độ của mối quan hệ tuyến tính giữa các biến. Một tương quan tham số sẽ thích hợp bất cứ khi nào các phép đo định lượng được thực hiện đồng thời trên hai hoặc nhiều biến, mối quan hệ giữa hai biến là tuyến tính và cả hai biến đều được phân phối chuẩn. Các mối tương quan phải luôn được kiểm tra trước khi thực hiện các phân tích đa biến phức tạp hơn, chẳng hạn như phân tích nhân tố (factor analysis) hoặc phân tích thành phần chính (principal component analysis). Mức độ của mối quan hệ tuyến tính giữa hai biến số có thể khó đánh giá từ biểu đồ phân tán và hệ số tương quan cung cấp một bản tóm tắt ngắn gọn hơn. Tuy nhiên, sẽ không khôn ngoan nếu cố gắng tính toán mối tương quan khi biểu đồ phân tán mô tả một mối quan hệ phi tuyến tính rõ ràng. Khi một nhà nghiên cứu quan tâm đến cả mức khoảng rộng và ý nghĩa của một mối tương quan thì r được sử dụng theo cách suy diễn như một ước lượng của mối tương quan dân số, ρ (rho).
Công thức tính hệ số tương quan Pearson trong hai biến x và y từ n mẫu như sau:
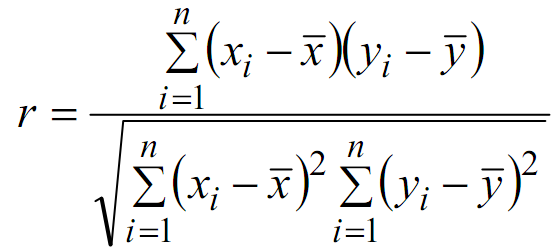
2. Giả thuyết vô hiệu và suy luận thống kê
Khi ước lượng kích thước của mối tương quan dân số, chúng ta có thể muốn kiểm tra xem nó có ý nghĩa thống kê hay không. Giả thuyết vô hiệu là H0: ρ = 0, nghĩa là, biến X không liên quan tuyến tính với biến Y. Giả thuyết thay thế là H1: ρ ≠ 0. Giả thuyết vô hiệu là một phép kiểm tra xem có bất kỳ mối quan hệ rõ ràng nào giữa các biến X và Y có thể phát sinh một cách tình cờ hay không. Phân phối mẫu của r là không chuẩn khi tương quan dân số lệch khỏi 0 và khi cỡ mẫu nhỏ (n <30). Khi đó, các kiểm định có ý nghĩa r được thay thế bằng một thống kê khác gọi là Fisher’s z.
3. Các giả định thống kê
Trong một số sách thống kê dành cho các nhà khoa học xã hội, người ta khẳng định rằng để sử dụng mối tương quan Pearson, cả hai biến phải có phân phối chuẩn, nhưng trong các văn bản khác, nó nói rằng phân phối của cả hai biến phải đối xứng (symmetrical) và đơn phương (unimodal) nhưng không nhất thiết phải chuẩn. Những ý kiến này gây hoang mang lớn cho các nhà nghiên cứu và cần được làm rõ. Nếu thống kê tương quan chỉ được sử dụng cho mục đích mô tả thì không cần thiết phải sử dụng các giả định chuẩn về hình thức (form) của phân phối dữ liệu. Các giả định duy nhất được yêu cầu là:
- các phép đo định lượng (mức khoảng hoặc mức tỷ lệ của phép đo) được thực hiện đồng thời trên hai hoặc nhiều biến ngẫu nhiên. Tức là hai biến phải được đo lường trên thang đo khoảng hoặc tỷ lệ. Tuy nhiên, cả hai biến không cần phải được đo lường trên cùng một thang đo (ví dụ, một biến có thể là tỷ lệ và một có thể là khoảng).
- các phép đo bắt cặp cho mỗi đối tượng (ví dụ, mỗi người tham gia) là độc lập. Ví dụ, bạn đã thu thập thời gian ôn tập (tính bằng giờ) và kết quả thi (đo từ 0 đến 100) từ 100 sinh viên được lấy mẫu ngẫu nhiên tại một trường đại học (tức là bạn có hai biến liên tục: “thời gian ôn tập” và “kỳ thi hiệu suất”). Mỗi người trong số 100 sinh viên sẽ có một giá trị về thời gian ôn tập (ví dụ: “sinh viên số 1” đã học trong “23 giờ”) và kết quả bài kiểm tra (ví dụ: “sinh viên số 1” đạt “81/100”). Do đó, bạn sẽ có 100 giá trị được ghép nối.
Các kết quả thu được sẽ mô tả mức độ mà mối quan hệ tuyến tính được áp dụng cho dữ liệu mẫu.
Ngoài ra, cần nhận xét thận trọng về việc sử dụng r. Đây không phải là những giả định nghiêm ngặt nhưng trong những tình huống nghiên cứu điển hình khi r hoặc là cần được giải thích một cách thận trọng, hoặc không nên sử dụng.
- Khi phương sai của hai thước đo rất khác nhau, thường liên quan đến các phạm vi khác nhau hoặc có thể là một phạm vi giới hạn cho một biến, thì mối tương quan mẫu sẽ bị ảnh hưởng. Ví dụ: nếu một biến bị hạn chế phạm vi, (một phần của phạm vi điểm số không được sử dụng hoặc không phù hợp) thì điều này sẽ có xu hướng làm giảm (thấp hơn) mối tương quan giữa hai biến.
- Khi có các giá trị ngoại lệ, r cần được giải thích một cách thận trọng.
- Khi các quan sát được lấy từ một nhóm không đồng nhất (heterogeneous). Nếu tốt nhất, dữ liệu nên là đồng nhất (homoscedasticity). Đồng nhất trong tương quan có nghĩa là các phương sai dọc theo đường của sự phù hợp nhất vẫn tương tự khi di chuyển dọc theo đường. Nếu các phương sai không giống nhau thì có phương sai thay đổi (hay còn gọi heteroscedasticity). Đồng nhất (hay độ co giãn đồng nhất) được thể hiện dễ dàng nhất bằng sơ đồ, như hình dưới đây:

- Khi dữ liệu thưa thớt (có quá ít số đo), r không nên được sử dụng. Với quá ít giá trị, không thể nói liệu mối quan hệ hai biến có tuyến tính hay không. Tương quan Pearson r là thích hợp nhất cho các mẫu lớn hơn (n> 30).
- Không nên sử dụng tương quan r khi các giá trị trên một trong các biến đã được cố định trước.
4. Phân tích tương quan Pearson r trong SPSS
Ví dụ, một nhà nghiên cứu muốn biết liệu kết quả kỳ thi viết cuối kì môn Toán giải thích có tương quan với thời gian ôn tập cuối kì của các sinh viên hay không. Có 20 sinh viên được mời tham gia một cuộc thử nghiệm, kể từ khi bài học của môn Toán giải tích kết kết đến ngày thi cuối kì, họ được đề nghị ghi lại tổng số giờ ôn bài (cộng dồn của mỗi ngày) dành cho môn Toán. Kết thúc kì thi, nhà nghiên cứu thu thập điểm số của 20 sinh viên này theo thang điểm 100, và tổng hợp theo bảng dưới đây.

Hai câu hỏi nghiên cứu được xem xét: i) Điểm thi viết cuối kì môn Toán giải thích có liên quan tuyến tính với số giờ ôn tập của các sinh viên hay không? và ii) Số giờ ôn tập của các sinh viên có liên quan tuyến tính với điểm thi viết cuối kì môn Toán giải thích hay không?
Các bước dưới đây hướng dẫn chúng ta cách phân tích Tương quan Pearson r trong Thống kê SPSS.
– Bước 1: Kiểm tra biểu đồ phân tán mô tả mối quan hệ giữa hai biến. Xin vui lòng đọc bài cách vẽ biểu đồ phân tán. Kết quả vẽ biểu đồ phân tán được trình bày trong hình dưới đây.
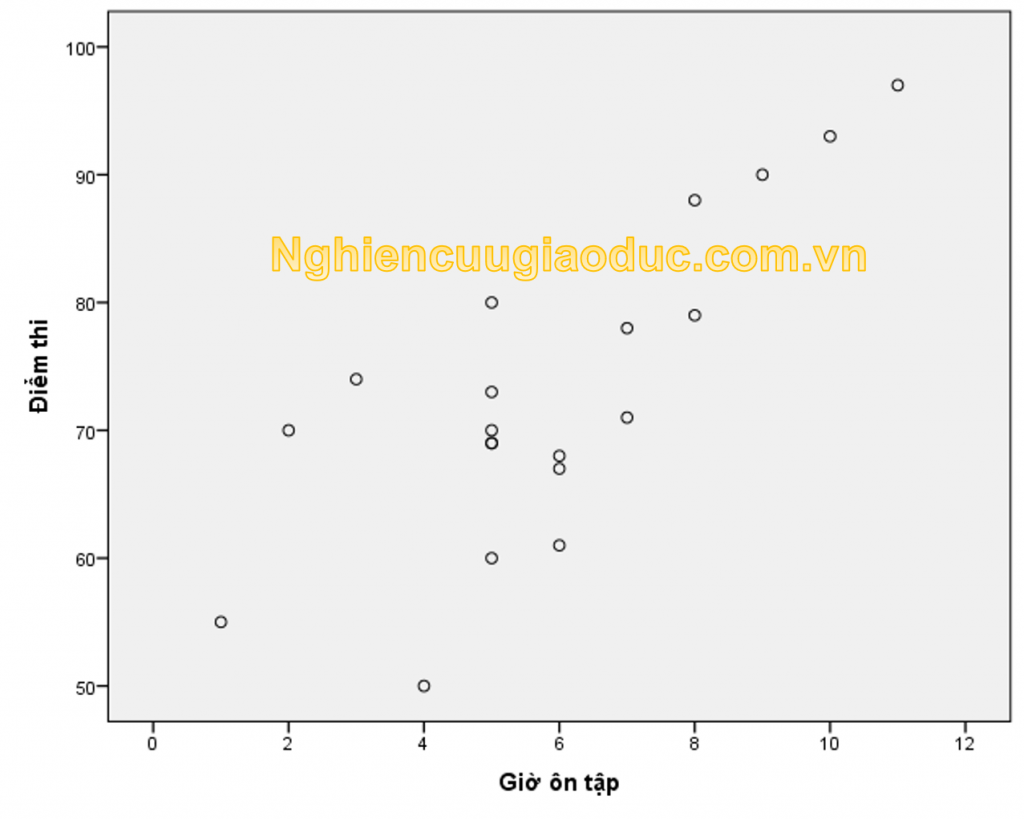
Nhận xét: Biểu đồ scatter giữa Điểm thi và Ôn tập gợi ý xu hướng gần đúng tuyến tính, nhưng cỡ mẫu là nhỏ để quan sát rõ ràng một đường tuyến tính. Trong thực tế, chúng ta cần một cỡ mẫu lớn hơn, ít nhất n > 30. Biểu đồ này cũng cho thấy một quan sát ngoại lệ rất rõ ràng (điểm gần giá trị 4 ở trục hoành).
– Bước 2: Khi biểu đồ phân tán dự đoán mối quan hệ tuyến tính, chúng ta tiến hành phân tích tương quan Pearson r. Click Analyze-> Correlate -> Bivariate…

– Bước 3: Trong hộp thoại Bivariate Correlations, chúng ta chuyển các biến cần kiểm tra tương quan với nhau vào hộp Variables. Chú ý check vào hộp Pearson trong vùng Correlation Coefficients. Sau đó nhấp OK để chạy kết quả.

Phân tích kết quả:
Bảng Correlations trình bày hệ số tương quan Pearson r, giá trị ý nghĩa p của nó và kích thước mẫu được tính toán. Trong ví dụ này, chúng ta có thể thấy rằng hệ số tương quan Pearson, r, là 0.78 và nó có ý nghĩa thống kê (p = 0.000).

Chúng ta có thể viết báo cáo rằng, một tương quan Pearson đã được chạy để xác định mối quan hệ tuyến tính giữa Điểm thi viết cuối kì môn Toán giải thích và số giờ ôn tập của các sinh viên. Kết quả cho thấy có mối tương quan thuận giữa Điểm thi viết cuối kì môn Toán giải thích và số giờ ôn tập của các sinh viên (r = 0.780, n = 20, p = 0.000).
– Bước 4: Kiểm tra ý nghĩa của hệ số tương quan r
Một khi mối tương quan đã được tính toán, nhà nghiên cứu có thể muốn biết khả năng xảy ra mối tương quan thu được này như thế nào, nghĩa là, đây có phải là sự xuất hiện tình cờ hay nó đại diện cho mối tương quan dân số đáng kể?
Để thực hiện việc này, r được chuyển đổi, và xác suất của công cụ ước lượng này dựa trên phân phối mẫu của thống kê t (t-statistic). Do đó, ý nghĩa của một hệ số tương quan Pearson thu được được đánh giá bằng cách sử dụng phân phối t (t-distribution) với n − 2 bậc tự do (df) và được cho bởi phương trình sau:

Giả thuyết vô hiệu được kiểm định là hai biến độc lập, tức là không có mối quan hệ tuyến tính giữa chúng, H0: ρ = 0. Giả thuyết thay thế là, H1: ρ ≠ 0.
Để trả lời câu hỏi, Có mối tương quan đáng kể nào, ở mức 5%, giữa điểm Điểm thi viết cuối kì môn Toán giải thích và số giờ ôn tập của các sinh viên không? t sẽ được tính như sau:

Tra bảng tới hạn của giá trị t (critical t-value) thu được giá trị là 2.101. Thống kê kiểm tra t là vượt quá giá trị tới hạn này, (5.433 > 2.101), và do đó giả thuyết vô hiệu bị bác bỏ. Chúng ta kết luận rằng mối tương quan có ý nghĩa ở mức 5%.
– Bước 5: Kiểm tra khoảng tin cậy của hệ số tương quan r
Khoảng tin cậy là dựa vào một sự chuyển đổi thống kê r thành thống kê Fisher’s z. Điều này không giống như độ lệch Z (Z-deviate) so với phân phối chuẩn (đôi khi được gọi là điểm Z). Để diễn giải khoảng tin cậy, điểm số Fisher’s z phải được chuyển đổi trở lại số liệu tương quan. Fisher’s z được đánh giá là:
Khoảng tin cậy (95%) cho mối tương quan lưỡng biến giữa Điểm thi viết cuối kì môn Toán giải thích và số giờ ôn tập của các sinh viên được tính bằng công thức:

Công thức chuyển đổi Fisher’s Z được định nghĩa là:

Áp dụng các công thức trong ví dụ (với r = 0.78), ta có:

Khoảng tin cậy (95%):

= 0.57 đến 1.52
Các giá trị này bây giờ phải được chuyển đổi trở lại số liệu ban đầu.

Nhận xét: Chúng ta có thể kết luận rằng chúng ta chắc chắn 95% rằng mối tương quan dân số là dương và nằm trong khoảng 0.515 đến 0.909. Khoảng tin cậy này không bao gồm giá trị 0, điều này cho thấy mối tương quan có ý nghĩa thống kê ở mức 5%.
Tài liệu tham khảo
- Coolican, H. (2018). Research methods and statistics in psychology. Routledge.
- Hanneman, R. A., Kposowa, A. J., & Riddle, M. D. (2012). Basic statistics for social research (Vol. 38). John Wiley & Sons.
- Jackson, S. L. (2015). Research methods and statistics: A critical thinking approach. Cengage Learning.
- McQueen, R. A., & Knussen, C. (2006). Introduction to research methods and statistics in psychology. Pearson education.
- Peers, I. (2006). Statistical analysis for education and psychology researchers: Tools for researchers in education and psychology. Routledge.
- Wagner III, W. E. (2019). Using IBM® SPSS® statistics for research methods and social science statistics. Sage Publications.
Từ khóa » Hệ Số Tương Quan Pearson Là Gì
-
Lý Thuyết Hệ Số Tương Quan Pearson - Phân Tích ... - Luận Văn 2S
-
Ý Nghĩa Hệ Số Tương Quan Pearson – Hướng Dẫn Cách Phân Tích Và ...
-
Correlation Coefficient - RPubs
-
Phân Tích Tương Quan Pearson Trong SPSS - Phạm Lộc Blog
-
Hệ Số Tương Quan Pearson Trong Spss: Định Nghĩa, Công Thức ...
-
Phân Tích Và đọc Kết Quả Tương Quan Pearson Trên SPSS
-
Phân Tích Tương Quan Pearson: Những điều Bạn Cần Biết
-
Những Lý Thuyết Về Tương Quan Pearson Trong SPSS Và Các Tiêu Chí
-
Hệ Số Tương Quan Pearson | Top #1 Cách Phân Tích Trong Stata
-
Ý Nghĩa Hệ Số Tương Quan Pearson - Cách Phân Tích Và ... - Trangwiki
-
Lý Thuyết Về Hệ Số Tương Quan Pearson Correlation Là Gì ...
-
Hệ Số Tương Quan (Correlation Coefficient) Là Gì? Ứng Dụng Của Hệ ...
-
Ý Nghĩa Và Phân Tích Hệ Số Tương Quan Pearson Chi Tiết Nhất