Những Lý Thuyết Về Tương Quan Pearson Trong SPSS Và Các Tiêu Chí

4.9/5 - (10 bình chọn)

Tương quan Pearson giúp chúng ta thực hiện các thống kê cơ bản như ước lượng điểm (kiểm định mức ý nghĩa), giải thích (sự ảnh hưởng của biến độc lập đối với biến phụ thuộc), dự báo (thông qua mô hình hồi quy tuyến tính), ước lượng độ tin cậy và tính hợp lý (validity). 

Mục lục Ẩn

• 1. Tương quan Pearson là gì?
• 2. Sự khác nhau giữa hồi quy và tương quan
• 3. Mục đích của việc chạy tương quan Pearson
• 4. Hướng dẫn chạy tương quan Pearson từ A đến Z
  • Bước 1: Vào menu Analyze-> Correlate -> Bivariate
  • Bước 2: Chọn các nhân tố vừa được tạo ở bước trên qua ô Variables bên phải. Xong bấm OK
  • Bước 3: Phân tích bảng kết quả
• 5. Giải thích ý nghĩa ma trận tương quan

1. Tương quan Pearson là gì?

Trong thống kê, hệ số tương quan có ý nghĩa đặc biệt quan trọng.

Tương quan hiểu một cách nôm na là mối quan hệ tương đối giữa các biến. Điều này có nghĩa là các biến có quan hệ với nhau trong một số điều kiện nhất định chứ không phải trong mọi trường hợp (quan hệ tuyệt đối).

Thông thường khi nói đến hệ số tương quan, chúng ta ngầm liên tưởng đến hệ số tương quan Pearson.

Hệ số tương quan Pearson giúp chúng ta thực hiện các thống kê cơ bản như ước lượng điểm (kiểm định mức ý nghĩa), giải thích (sự ảnh hưởng của biến độc lập đối với biến phụ thuộc), dự báo (thông qua mô hình hồi quy tuyến tính), ước lượng độ tin cậy và tính hợp lý (validity).

Nó cũng có thể thiết lập và kiểm định các mô hình có chứa các biến tiềm ẩn và các biến có thể đo lường được. Mặc dù hệ số này có ảnh hưởng lớn trong lĩnh vực thống kê nhưng cũng tồn tại một số hệ số khác được sử dụng tùy thuộc vào biến đo lường.

2. Sự khác nhau giữa hồi quy và tương quan

Nhiều bạn nghĩ rằng phương trình hồi quy và phương trình tương quan là một. Tuy nhiên thực tế lại không phải như vậy. Chúng khác nhau cả về mục đích và kỹ thuật.

Tương quan: Có tác động 2 chiều giữa 2 hay nhiều biến, ở đây sẽ không phân biệt biến nội sinh và ngoại sinh (biến độc lập và biến phụ thuộc), chúng có tính chất đối xứng. Nghĩa là chúng ta sẽ phải xem xét tác động qua lại giữa cả 2 hay nhiều biến với nhau.

• Ví dụ: Mức độ quan hệ giữa nghiện thuốc lá và ung thư phổi, giữa kết quả thi môn Lý và môn Toán.

Hồi quy: Chỉ có tác động một chiều của biến độc lập lên biến phụ thuộc. Biến phụ thuộc là đại lượng ngẫu nhiên

Tóm lại, hồi quy thì tương quan (Hay nói cách khác, để được hồi quy thì trước hết phải tương quan), còn tương quan thì chưa chắc đã hồi quy. 

3. Mục đích của việc chạy tương quan Pearson

Mục đích của việc chạy tương quan Pearson là kiểm tra mối tương quan tuyến tính chặt chẽ giữa biến phụ thuộc với các biến độc lập. Bởi vì điều kiện để hồi quy là trước nhất phải tương quan. Tiếp đến đó là nhận diện vấn đề đa cộng tuyến khi các biến độc lập cũng có tương quan mạnh với nhau. Dấu hiệu đa cộng tuyến sẽ được xem xét khi phân tích hồi quy (Kiểm tra hệ số VIF)

Cách đọc kết quả phân tích tương quan Pearson

Hệ số tương quan (r) là một chỉ số thống kê đo lường mối liên hệ tương quan giữa hai biến số, như giữa MỨC ĐỘ HÀI LÒNG (y) và TIỀN LƯƠNG (x). Hệ số tương quan có giá trị từ -1 đến 1:

• Hệ số tương quan bằng 0 (hay gần 0) có nghĩa là hai biến số không có liên hệ gì với nhau
• Hệ số bằng -1 hay 1 có nghĩa là hai biến số có một mối liên hệ tuyệt đối
• Hệ số tương quan là âm (r <0) có nghĩa là khi x tăng cao thì y giảm (và ngược lại, khi x giảm thì y tăng)
• Hệ số tương quan là dương (r > 0) có nghĩa là khi x tăng cao thì y cũng tăng, và khi x tăng cao thì y cũng tăng theo.

Có nhiều hệ số tương quan, hệ số tương quan thông dụng nhất: Hệ số tương quan Pearson r, được định nghĩa như sau:

Cho hai biến số x và y từ n mẫu, hệ số tương quan Pearson được ước tính bằng công thức sau đây:

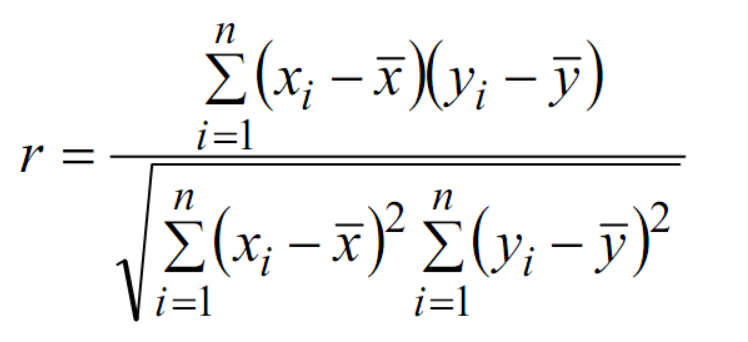
Trong phân tích áp dụng cho luận văn, kiểm định hệ số tương quan Pearson dùng để kiểm tra mối liên hệ tuyến tính giữa các biến độc lập và biến phụ thuộc. Nếu các biến độc lập với nhau có tương quan chặt thì phải lưu ý đến vấn đề đa cộng tuyến khi phân tích hồi quy (giả thuyết H0: hệ số tương quan bằng 0).

Nếu bạn vẫn chưa thực sự tự tin về kiến thức có hạn của mình, bạn hãy cùng Luận Văn Việt tìm hiểu dịch vụ chạy SPSS kinh nghiệm 20 năm với hơn 20+ lĩnh vực ứng dụng cùng đội ngũ chuyên gia chất lượng.

4. Hướng dẫn chạy tương quan Pearson từ A đến Z

Bước 1: Vào menu Analyze-> Correlate -> Bivariate

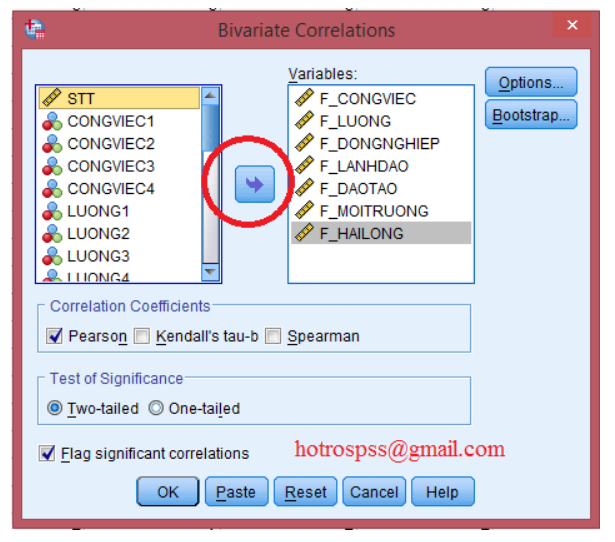
Bước 2: Chọn các nhân tố vừa được tạo ở bước trên qua ô Variables bên phải. Xong bấm OK

Bước 3: Phân tích bảng kết quả

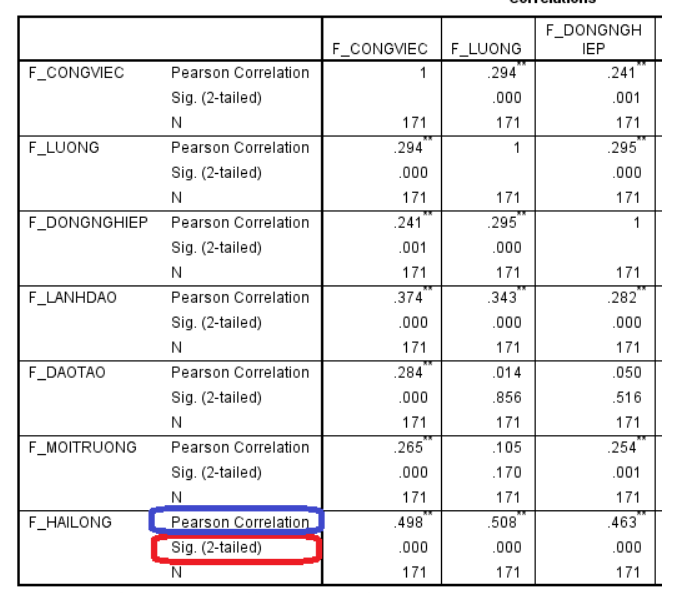
Ô màu xanh: hệ số tương quan Pearson

Ô màu đỏ: significant của kiểm định Pearson.

Giả thuyết H0: hệ số tương quan bằng 0. Do đó nếu Sig. Này bé hơn 5% ta có thể kết luận được là hai biến có tương quan với nhau. Hệ số tương quan càng lớn tương quan càng chặt. nếu Sig. này lớn hơn 5% thì hai biến không có tương quan với nhau.

Vì một trong những điều kiện cần để phân tích hồi quy là biến độc lập phải có tương quan với biến phụ thuộc, nên nếu ở bước phân tích tương quan này biến độc lập không có tương quan với biến phụ thuộc thì ta loại biến độc lập này ra khỏi phân tích hồi quy.

Kết quả phân tích tương quan Pearson cho thấy một số biến độc lập có sự tương quan với nhau. Do đó khi phân tích hồi quy cần phải chú ý đến vấn đề đa cộng tuyến. Các biến độc lập có tương quan với biến phụ thuộc và do đó sẽ được đưa vào mô hình để giải thích cho biến phụ thuộc.

Hệ số tương quan Pearson càng tiến về 1 càng tương quan mạnh. Ngược lại, hệ số này càng tiến gần về 0 thì tương quan càng yếu.

Bạn cần lưu ý đến giá trị sig: Nếu bạn chọn mức ý nghĩa 1% thì giá trị sig phải < 0.01, còn nếu bạn chọn mức ý nghĩa là 5% thì sig < 0.05 tương ứng với các dấu (*) được đánh dấu trên hệ số tương quan r. Chú thích ở 2 hàng cuối cùng trong bảng Correlation

**. Correlation is significant at the 0.01 level (2-tailed)

*. Correlation is significant at the 0.05 level (2-tailed)

5. Giải thích ý nghĩa ma trận tương quan

* Với hệ số Pearson Correlation nói lên mức độ tương quan giữa các biến với nhau trong mô hình. Hệ số tương quan càng lớn nói lên mức độ tương quan càng cao, điều này có thể dẫn tới hiện tượng đa cộng tuyến khi kiểm định mô hình hồi quy.

* Hệ số Sig: Nói lên tính phù hợp của hệ số tương quan giữa các biến theo phép kiểm định F với một độ tin cậy cho trước.

Trên đây là bài viết tham khảo cung cấp cho bạn những thông tin chi tiết về Tương quan Pearson là gì? Chạy tương quan Pearson như thế nào? Nếu bạn còn bất kỳ thắc mắc và khó khăn nào trong quá trình nghiên cứu hệ số này, hay gọi đến Luận Văn Việt theo hotline 0915 686 999 hoặc qua email luanvanviet.group@gmail.com để được tư vấn và hỗ trợ.

Nguồn: Luận Văn Việt

3/5 (2 Reviews) Lưu Hà Chi( Content Leader )

CEO Helen Lưu Hà Chi – Nhà sáng lập website luanvanviet.com , nơi cung cấp các dịch vụ viết thuê luận văn thạc sĩ, tốt nghiệp, tiểu luận, essay, Assignment, cùng với các giải pháp chuyên sâu về xử lý số liệu bao gồm SPSS, STATA, EVIEWS, và SmartPLS.

Post Views: 13.560