Các Dạng Toán đường Thẳng Và Mặt Phẳng Trong Không Gian, Quan ...
Có thể bạn quan tâm
Download.vn Hướng dẫn sử dụng, mẹo vặt, thủ thuật phần mềm tài liệu và học tập Thông báo Mới
Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -1- CHƢƠNG II.ĐƢỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONGChủđề 1: ĐẠI CƢƠNG VỀĐƢỜNG THẲNG VÀ MẶT PHẲNGDạng toán 1: XÁC ĐỊNH GIAO TUYẾN CỦA HAI MẶT PHẲNGPhương pháp: Muốn tìm giao tuyến của hai mặt phẳng αvàβta đi tìm hai điểm chung I; J của mpαvàmpβ.Kí hiệu:mpmpIJαβKhi tìm điểm chung ta chú ý: Cách gọi tên hai mặt phẳng để phát hiện điểm chung. Md và d mpαMαabMPa;bααM là điểm chung của (P) và α.BÀI TẬP:Bài tập 1: Cho tứ diện ABCD với E là trung điểm của AB. Hãy xác định giao tuyến của mặt phẳng (ECD) với các mặt phẳng (ABC), (ABD), (BCD), (ACD). Bài tập 2: Cho tứ diện SABC và một điểm Itrên đoạn SA, d là đường thẳng trong (ABC) cắt AB, BC tại J và K. Tìm giao tuyến của mặt phẳng (I ;d) với các mặt phẳng sau: (SAB),(SAC), (SBC).Bài tập 3: Cho tứ giác lồi ABCD với hai cặp cạnh đối không song song và điểm S không nằm trong mặt phẳng chứa tứ giác. Tìm giao tuyến của các mặt phẳng:a) (SAC) và (SBD). b) (SAB) và (SCD). c) (SAD) và (SBC). Bài tập 4: Cho hình chóp S.ABCDE. Hãy xác định giao tuyến của mặt phẳng (SAC) với các mặt phẳng (SAD), (SCE). Bài tập 5: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi, M là điểm trên cạnh CD. Tìm giao tuyến của các cặp mặt phẳng: a) (SAM) và (SBD). b) (SBM) và (SAC).JI
Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -2- Bài tập 6: Cho tứ diện ABCD, M là điểm thuộc miền trong tam giác ABC, N là điểm thuộc miền trong tam giác ACD. Tìm giao tuyến của các cặp mặt phẳng: a) (AMN) và (BCD) b) (CMN) và (ABD).Bài tập 7: Cho tứ diện ABCD. Điểm M nằm trên AB sao cho AM = 41MB, N nằm trên ACsao cho AN = 3NC, điểm I nằm trong mặt phẳng (BCD). Tìm giao tuyến của các cặp mặt phẳng: a) (MNI) và (BCD). b) (MNI) và (ABD). c) (MNI) và (ACD).Bài tập 8: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AD và BC. a) Tìm giao tuyến của mặt phẳng (IBC) và mặt phẳng (JAD). b) M là điểm trên AB và N là điểm trên AC. Tìm giao tuyến của (IBC) và (DMN)Bài tập 8: Cho tứ diện SABC. Gọi G là trọng tâm của tam giác ABC và M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Điểm E, F lần lượt là 2 điểm trên SB và SC. Xác định giao tuyến của các cặp mặt phẳng sau: a) (SAN) và (SBP). b) (SCM) và (SBP). c) (AEF) và (ABC). d) (AEF) và (ASG). Bài tập 10: Cho hình chóp S.ABCD có đáy là hình thang với hai đáy là AB và CD. Tìm giao tuyến của: a) (SAD) và (SBC). b) (SAC) và (SBD)Bài tập 11: Hình chóp S.ABCD có đáy ABCD là hình thang hai đáy là AD và BC. Gọi M, N là trung điểm AB, CD và G là trọng tâm SAD. Tìm giao tuyến của các cặp mặt phẳng: a) (GMN) và (SAC). b) (GMN) và (SBC).Dạng toán 2: TÌM GIAO ĐIỂM CỦA ĐƢỜNG THẲNG VÀ MẶT PHẲNGPhương pháp: Giả sử phải tìm giao điểm mpd?αPhƣơng pháp 1: Bƣớc 1:TìmaαBƣớc 2: Chỉ ra được a, d nằm trong cùng mặt phẳng vàchúng cắt nhau tại M: dα= M (hình vẽ)Phƣơng pháp 2: Bƣớc 1:Tìmβchứa d thích hợp. Bƣớc 2: Tìm giao tuyếnacủa αvàβBƣớc 3: Xác định giao điểm của a và d.adMadM
Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -3- BÀI TẬP:Bài tập 1: Cho tứ diện SABC với M, N lần lượt là các điểm nằm trong (SAB) và (SBC). Xác định giao điểm của MN và mặt phẳng (ABC). Bài tập 2: Cho tứ diện ABCD. Gọi M là trung điểm AB, N và P lần lượt là các điểm nằm trên AC, AD sao cho AN : AC = 3 : 4, AP : AD = 2 : 3. Gọi Q là trung điểm NP . Tìm giaođiểm:a) MN với (BCD). b) BD với (MNP). c) MQ với (BCD).Bài tập 3: Cho tứ diện ABCD. Gọi M, Nlần lượt là trung điểm của AC và BC. Trên đoạn BD lấy P sao cho BP= 2PD. Tìm giao điểm của: a) CD với (MNP). b) AD với (MNP).Bài tập 4: Cho hình chóp S.ABC, O là điểm thuộc miền trong tam giác ABC. Điểm D và E là các điểm nằm trên cạnh SB, SC.Tìm giao điểm của: a) DE với (SAO). b) SO với (ADE).Bài tập 5: Cho tứ diện SABC. Gọi I, H lần lượt là trung điểm SA và AB. Trên đoạn SC lấy điểm K sao cho CK = 3KS.a) Tìm giao điểm của đường thẳng BC với (IHK). b) Gọi M là trung điểm HI. Tìm giao điểm của đường thẳng KM với (ABC).Bài tập 6: Cho hình chóp S.ABCD đáy là hình thang ABCD đáy lớn AB. Gọi I, J, K là ba điểm trên cạnh SA, SB, SC. a) Tìm giao điểm IK và (SBD). b) Giao điểm (IJK) và SD; SC. Bài tập 7: Gọi I, J lần lượt là hai điểm nằm trên mp(ABC) và mp(ABD) của tứ diện ABCD. M là điểm tuỳ ý trên cạnh CD. Tìm giao điểm IJ và mặt phẳng (AMB).Bài tập 8: Hình chóp S.ABCD đáy là hình bình hành với M là trung điểm SD. a) Tìm giao điểm I của BM và (SAC). Chứng minh: BI = 2IM. b) Tìm giao điểm J của của SA và (BCM). Chứng minh: J là trung điểm SA.c) N là điểm tuỳ ý trên cạnh BC. Tìm giao điểm của MN với (SAC).Bài tập 9: Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm BD). Tìm giao điểm của đường thẳngAD và mặt phẳng (MNK). Bài tập 10: Cho hình chóp S.ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) và các cạnh của hình chóp. Bài tập 11: Cho hình chóp S.ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD và mặt phẳng (AMN).Chia sẻ bởi: 
Trịnh Thị Thanh Xóa Đăng nhập để GửiFacebook
Twitter
- Tất cả
-
Học tập -
Tài liệu -
Hướng dẫn
-
-
Học tập -
Tài liệu -
Hướng dẫn -
Tác phẩm Văn học -
Đề thi -
Tài liệu Giáo viên -
Học tiếng Anh
-
- 6
Các dạng toán đường thẳng và mặt phẳng trong không gian, quan hệ song song là tài liệu cực kì hữu ích mà Download.vn muốn giới thiệu đến các bạn học sinh lớp 11 cùng tham khảo.
Tài liệu bao gồm 32 trang tổng hợp các dạng bài tập chương II lớp 11 môn Toán. Tài liệu giúp các bạn học sinh lớp 11 có thêm nhiều tài liệu tham khảo củng cố kiến thức chương II để đạt được kết quả cao trong các bài kiểm tra, bài thi sắp tới. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Các dạng toán đường thẳng và mặt phẳng trong không gian, quan hệ song song
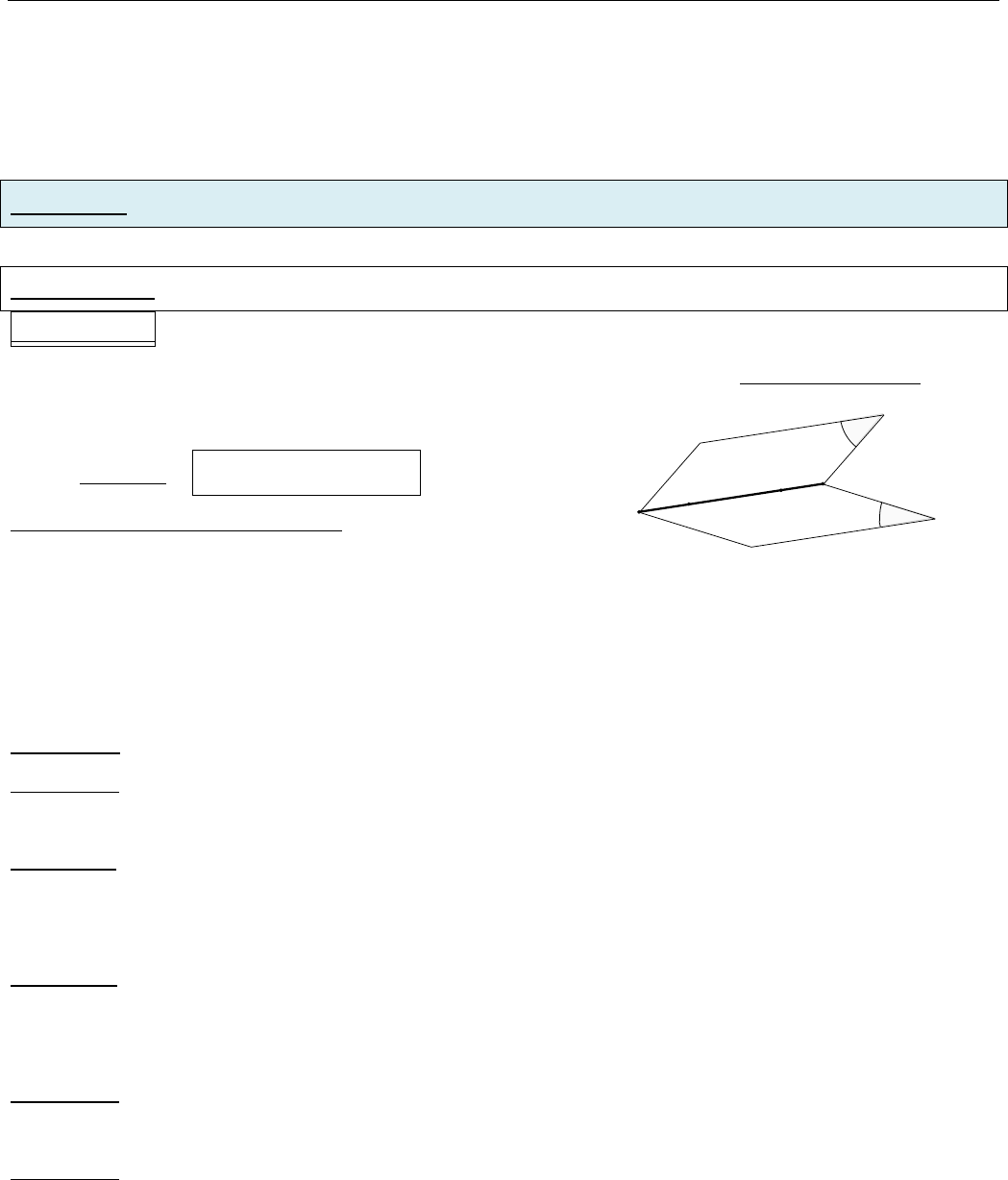Chuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -1- CHƢƠNG II.ĐƢỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONGChủđề 1: ĐẠI CƢƠNG VỀĐƢỜNG THẲNG VÀ MẶT PHẲNGDạng toán 1: XÁC ĐỊNH GIAO TUYẾN CỦA HAI MẶT PHẲNGPhương pháp: Muốn tìm giao tuyến của hai mặt phẳng αvàβta đi tìm hai điểm chung I; J của mpαvàmpβ.Kí hiệu:mpmpIJαβKhi tìm điểm chung ta chú ý: Cách gọi tên hai mặt phẳng để phát hiện điểm chung. Md và d mpαMαabMPa;bααM là điểm chung của (P) và α.BÀI TẬP:Bài tập 1: Cho tứ diện ABCD với E là trung điểm của AB. Hãy xác định giao tuyến của mặt phẳng (ECD) với các mặt phẳng (ABC), (ABD), (BCD), (ACD). Bài tập 2: Cho tứ diện SABC và một điểm Itrên đoạn SA, d là đường thẳng trong (ABC) cắt AB, BC tại J và K. Tìm giao tuyến của mặt phẳng (I ;d) với các mặt phẳng sau: (SAB),(SAC), (SBC).Bài tập 3: Cho tứ giác lồi ABCD với hai cặp cạnh đối không song song và điểm S không nằm trong mặt phẳng chứa tứ giác. Tìm giao tuyến của các mặt phẳng:a) (SAC) và (SBD). b) (SAB) và (SCD). c) (SAD) và (SBC). Bài tập 4: Cho hình chóp S.ABCDE. Hãy xác định giao tuyến của mặt phẳng (SAC) với các mặt phẳng (SAD), (SCE). Bài tập 5: Cho hình chóp S.ABCD có đáy ABCD là một tứ giác lồi, M là điểm trên cạnh CD. Tìm giao tuyến của các cặp mặt phẳng: a) (SAM) và (SBD). b) (SBM) và (SAC).JIChuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -2- Bài tập 6: Cho tứ diện ABCD, M là điểm thuộc miền trong tam giác ABC, N là điểm thuộc miền trong tam giác ACD. Tìm giao tuyến của các cặp mặt phẳng: a) (AMN) và (BCD) b) (CMN) và (ABD).Bài tập 7: Cho tứ diện ABCD. Điểm M nằm trên AB sao cho AM = 41MB, N nằm trên ACsao cho AN = 3NC, điểm I nằm trong mặt phẳng (BCD). Tìm giao tuyến của các cặp mặt phẳng: a) (MNI) và (BCD). b) (MNI) và (ABD). c) (MNI) và (ACD).Bài tập 8: Cho tứ diện ABCD. Gọi I, J lần lượt là trung điểm của AD và BC. a) Tìm giao tuyến của mặt phẳng (IBC) và mặt phẳng (JAD). b) M là điểm trên AB và N là điểm trên AC. Tìm giao tuyến của (IBC) và (DMN)Bài tập 8: Cho tứ diện SABC. Gọi G là trọng tâm của tam giác ABC và M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Điểm E, F lần lượt là 2 điểm trên SB và SC. Xác định giao tuyến của các cặp mặt phẳng sau: a) (SAN) và (SBP). b) (SCM) và (SBP). c) (AEF) và (ABC). d) (AEF) và (ASG). Bài tập 10: Cho hình chóp S.ABCD có đáy là hình thang với hai đáy là AB và CD. Tìm giao tuyến của: a) (SAD) và (SBC). b) (SAC) và (SBD)Bài tập 11: Hình chóp S.ABCD có đáy ABCD là hình thang hai đáy là AD và BC. Gọi M, N là trung điểm AB, CD và G là trọng tâm SAD. Tìm giao tuyến của các cặp mặt phẳng: a) (GMN) và (SAC). b) (GMN) và (SBC).Dạng toán 2: TÌM GIAO ĐIỂM CỦA ĐƢỜNG THẲNG VÀ MẶT PHẲNGPhương pháp: Giả sử phải tìm giao điểm mpd?αPhƣơng pháp 1: Bƣớc 1:TìmaαBƣớc 2: Chỉ ra được a, d nằm trong cùng mặt phẳng vàchúng cắt nhau tại M: dα= M (hình vẽ)Phƣơng pháp 2: Bƣớc 1:Tìmβchứa d thích hợp. Bƣớc 2: Tìm giao tuyếnacủa αvàβBƣớc 3: Xác định giao điểm của a và d.adMadMChuyên đề HÌNH HỌC KHÔNG GIAN Hình học 11 CB Sưu tầm và biên tập: LÊ BÁ BẢO…0935.785.115…. CLB Giáo viên trẻ TP Huế -3- BÀI TẬP:Bài tập 1: Cho tứ diện SABC với M, N lần lượt là các điểm nằm trong (SAB) và (SBC). Xác định giao điểm của MN và mặt phẳng (ABC). Bài tập 2: Cho tứ diện ABCD. Gọi M là trung điểm AB, N và P lần lượt là các điểm nằm trên AC, AD sao cho AN : AC = 3 : 4, AP : AD = 2 : 3. Gọi Q là trung điểm NP . Tìm giaođiểm:a) MN với (BCD). b) BD với (MNP). c) MQ với (BCD).Bài tập 3: Cho tứ diện ABCD. Gọi M, Nlần lượt là trung điểm của AC và BC. Trên đoạn BD lấy P sao cho BP= 2PD. Tìm giao điểm của: a) CD với (MNP). b) AD với (MNP).Bài tập 4: Cho hình chóp S.ABC, O là điểm thuộc miền trong tam giác ABC. Điểm D và E là các điểm nằm trên cạnh SB, SC.Tìm giao điểm của: a) DE với (SAO). b) SO với (ADE).Bài tập 5: Cho tứ diện SABC. Gọi I, H lần lượt là trung điểm SA và AB. Trên đoạn SC lấy điểm K sao cho CK = 3KS.a) Tìm giao điểm của đường thẳng BC với (IHK). b) Gọi M là trung điểm HI. Tìm giao điểm của đường thẳng KM với (ABC).Bài tập 6: Cho hình chóp S.ABCD đáy là hình thang ABCD đáy lớn AB. Gọi I, J, K là ba điểm trên cạnh SA, SB, SC. a) Tìm giao điểm IK và (SBD). b) Giao điểm (IJK) và SD; SC. Bài tập 7: Gọi I, J lần lượt là hai điểm nằm trên mp(ABC) và mp(ABD) của tứ diện ABCD. M là điểm tuỳ ý trên cạnh CD. Tìm giao điểm IJ và mặt phẳng (AMB).Bài tập 8: Hình chóp S.ABCD đáy là hình bình hành với M là trung điểm SD. a) Tìm giao điểm I của BM và (SAC). Chứng minh: BI = 2IM. b) Tìm giao điểm J của của SA và (BCM). Chứng minh: J là trung điểm SA.c) N là điểm tuỳ ý trên cạnh BC. Tìm giao điểm của MN với (SAC).Bài tập 9: Cho tứ diện ABCD có các điểm M và N lần lượt là trung điểm của AC và BC. Lấy điểm K thuộc đoạn BD (K không là trung điểm BD). Tìm giao điểm của đường thẳngAD và mặt phẳng (MNK). Bài tập 10: Cho hình chóp S.ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) và các cạnh của hình chóp. Bài tập 11: Cho hình chóp S.ABCD. Gọi M, N lần lượt là các điểm thuộc các cạnh SC và BC. Tìm giao điểm của đường thẳng SD và mặt phẳng (AMN).Chia sẻ bởi: Trịnh Thị Thanh Download
Liên kết tải vềLink Download chính thức:
Các dạng toán đường thẳng và mặt phẳng trong không gian, quan hệ song song DownloadTìm thêm: Toán 11Có thể bạn quan tâm
-
Mẫu báo cáo kiểm điểm tập thể năm 2023
50.000+ -
Kế hoạch bồi dưỡng thường xuyên cá nhân Giáo viên (13 mẫu)
100.000+ -
Soạn bài Trình bày ý kiến về những hoạt động thiện nguyện vì cộng đồng - Kết nối tri thức 7
10.000+ 4 -
Đề thi giáo viên dạy giỏi THCS cấp huyện
10.000+ -
KHTN Lớp 6 Bài 19: Cơ thể đơn bào và cơ thể đa bào
50.000+ 8 -
Toán 6 Bài 4: Phép trừ số nguyên. Quy tắc dấu ngoặc
50.000+ 1 -
Đáp án cuộc thi Tìm hiểu chính sách, pháp luật về phòng, chống tham nhũng, tiêu cực năm 2023
50.000+ -
Tập làm văn lớp 4: Tả cánh diều tuổi thơ
50.000+ -
Phiếu đánh giá và phân loại công chức mới nhất
50.000+ -
Tên con gái đẹp năm 2022 đầy ý nghĩa
10.000+
Xóa Đăng nhập để GửiMới nhất trong tuần
Hướng dẫn sử dụng máy tính cầm tay giải nhanh trắc nghiệm lượng giác
Hướng dẫn tìm công thức truy hồi của dãy số
Góc giữa hai mặt phẳng: Định nghĩa, cách xác định và Bài tập (có đáp án)
Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 11 năm 2023 - 2024
Phương trình tiếp tuyến
Toán 11 Bài 17: Hàm số liên tục
Phiếu bài tập cuối tuần Toán 11
Bài tập đường thẳng và mặt phẳng trong không gian, quan hệ song song
Giá trị lớn nhất, nhỏ nhất của hàm số lượng giác
Tính tuần hoàn của hàm số lượng giác
Tài khoản
Gói thành viên
Giới thiệu
Điều khoản
Bảo mật
Liên hệ
DMCA
Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Dịch Vọng Hậu, Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: [email protected]. Bản quyền © 2024 download.vn.Từ khóa » Bài Tập Về Chương 2 Hình Học 11
-
Bài Tập Hình Học 11 Chương 2 đầy đủ Các Bài Lư Sĩ Pháp
-
Bài Tập Và Lý Thuyết Chương 2 Hình Học Lớp 11 - Đặng Việt Đông
-
BÀI TẬP HÌNH HỌC KHÔNG GIAN LỚP 11 CHƯƠNG 2 CÓ LÒI GIẢI ...
-
Kiểm Tra Hình Học 11 Chương 2
-
Giải Toán 11 Bài Tập ôn Tập Chương II
-
Bài Tập Hình Học 11 Chương 2
-
Giải Toán 11 Bài Tập ôn Tập Chương 2
-
Giải Bài Tập SGK Hình Học 11 Chương 2 Quan Hệ Song Song (Full)
-
Giải SBT Hình Học 11 - Chương 2: Đường Thẳng Và Mặt Phẳng Trong ...
-
Giải Bài Tập Hình Học 11 Chương 2 Bài 1 Đại Cương Về đường ...
-
Hình Học 11 Chương 2: Đường Thẳng Và Mặt Phẳng Trong Không ...
-
Giải Bài: Ôn Tập Chương II | Hình Học 11 Trang 77 - 80 - Tech12h
-
Chương 2: Đường Thẳng Và Mặt Phẳng Trong Không Gian. Quan Hệ ...
-
Bài Tập Chương 2 Hình Học 11