Chia đa Thức Cho đa Thức: Lý Thuyết & Bài Tập

Trang chủ » Cách Chia đa Thức Cho đa Thức Có Dư » Chia đa Thức Cho đa Thức: Lý Thuyết & Bài Tập

Có thể bạn quan tâm

Chia đa thức cho đa thức là một trong những dạng toán trọng tâm thường xuất hiện trong các bài kiểm tra, bài thi lớp 8.

Cách chia đa thức cho đa thức tổng hợp toàn bộ kiến thức lý thuyết, cách tính, ví dụ minh họa kèm theo một số bài tập tự luyện. Thông qua tài liệu này giúp học sinh củng cố, nắm vững chắc kiến thức nền tảng, vận dụng với các bài tập cơ bản để đạt được kết quả cao trong các kì thi sắp tới. Ngoài ra để nâng cao kỹ năng giải toán các bạn xem thêm tài liệu: bài tập hằng đẳng thức lớp 8, bài tập phân tích đa thức thành nhân tử.

Chuyên đề Chia đa thức cho đa thức

  • I. Lý thuyết chia đa thức cho đa thức
  • II. Ví dụ chia đa thức cho đa thức
  • III. Cách chia đa thức cho đa thức nâng cao
  • IV. Bài tập chia đa thức cho đa thức lớp 8

I. Lý thuyết chia đa thức cho đa thức

Ta trình bày phép chia tương tự như cách chia các số tự nhiên. Với hai đa thức A và B của một biến, B ≠ 0 tồn tại duy nhất hai đa thức Q và R sao cho:

A = B . Q + R, với R = 0 hoặc R≠ 0 có bậc bé hơn bậc của B

- Nếu R = 0, ta được phép chia hết.

Nếu R ≠ 0, ta được phép chia có dư.

Có thể dùng hằng đẳng thức để rút gọn phép chia

(A^{3}+B^{3}):(A+B)=A^{2}-AB+B^{2}\((A^{3}+B^{3}):(A+B)=A^{2}-AB+B^{2}\)

(A^{3}-B^{3}):(A-B)=A^{2}+AB+B^{2}\((A^{3}-B^{3}):(A-B)=A^{2}+AB+B^{2}\)

(A^{2}-B^{2}):(A+B)=A-B\((A^{2}-B^{2}):(A+B)=A-B\)

II. Ví dụ chia đa thức cho đa thức

Ví dụ 1: Áp dụng hằng đẳng thức đáng nhớ để thực hiện phép chia:

(125x^{3} + 1) : (5x + 1)\((125x^{3} + 1) : (5x + 1)\)

(x^{2} –2xy + y^{2}) : (y – x)\((x^{2} –2xy + y^{2}) : (y – x)\)

Cách dẫn giải như sau

(125x^{3} + 1) : (5x + 1) = [(5x)^{3} + 1] : (5x + 1) =(5x)^{2}-5x+1 = 25x^{2}-5x+1\((125x^{3} + 1) : (5x + 1) = [(5x)^{3} + 1] : (5x + 1) =(5x)^{2}-5x+1 = 25x^{2}-5x+1\)

(x^{2}-2xy+y^{2}) : (y-x) = (x-y)^{2}: [-(x-y)] =-(x-y)=y-x\((x^{2}-2xy+y^{2}) : (y-x) = (x-y)^{2}: [-(x-y)] =-(x-y)=y-x\)

Hoặc (x^{2}–2xy+y^{2}):(y-x) = (y^{2}-2xy+x^{2}) : (y-x)\((x^{2}–2xy+y^{2}):(y-x) = (y^{2}-2xy+x^{2}) : (y-x)\)

Ví dụ 2: Thực hiện phép chia đa thức f\left( x \right) = {x^4} - 2{x^3} - 3{x^2} + 7x - 2\(f\left( x \right) = {x^4} - 2{x^3} - 3{x^2} + 7x - 2\) cho đa thức x + 3\(x + 3\).

Lời giải:

Lưu ý rằng: nếu chia cho đa thức x + 3\(x + 3\) thì \alpha = 3\(\alpha = 3\), còn nếu chia cho đa thức x + 3\(x + 3\) thì \alpha = - 3\(\alpha = - 3\)

Dựa vào hướng dẫn trên ta sẽ có sơ đồ Hoocne như sau:

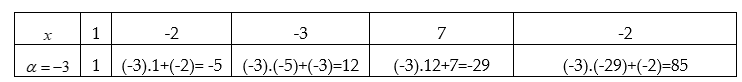
Đa thức g\left( x \right)\(g\left( x \right)\) tìm được ở đây chính là:

g\left( x \right) = 1.{x^3} + \left( { - 5} \right).{x^2} + 12.x + \left( { - 29} \right)\(g\left( x \right) = 1.{x^3} + \left( { - 5} \right).{x^2} + 12.x + \left( { - 29} \right)\)và r = 85\(r = 85\)

Vậy khi chia đa thức f\left( x \right) = {x^4} - 2{x^3} - 3{x^2} + 7x - 2\(f\left( x \right) = {x^4} - 2{x^3} - 3{x^2} + 7x - 2\) cho đa thức x + 3\(x + 3\) ta được:

f\left( x \right) = \left( {x + 3} \right)\left( {{x^3} - 5{x^2} + 12x - 29} \right) + 85\(f\left( x \right) = \left( {x + 3} \right)\left( {{x^3} - 5{x^2} + 12x - 29} \right) + 85\)

* Tuy nhiên không phải lúc nào bài toán cũng yêu cầu thực hiện phép chia đa thức bằng sơ đồ Hoocne. Vậy thì trong một số trường hợp sau đây ta có thể sử dụng sơ đồ:

+ Chia đa thức cho đa thức một cách nhanh nhất.

+ Tìm nghiệm của phương trình bậc 3, phương trình bậc 4, phương trình bậc cao.

+ Phân tích đa thức thành nhân tử (với những đa thức có bậc lớn hơn 2).

III. Cách chia đa thức cho đa thức nâng cao

Tìm thương và dư trong phép chia đa thức

- Phương pháp: từ điều kiện đề bài đã cho, đặt phép chia A:B được kết quả là thương Q và dư R.

Tìm điều kiện của m để đa thức A chia hết cho đa thức B

Ví dụ: Tìm giá trị nguyên của n để biểu thức 4n^{3}-4n^{2}-n+4\(4n^{3}-4n^{2}-n+4\) chia hết cho biểu thức 2n+1

Cách giải

Thực hiện phép chia 4n^{3}-4n^{2}-n+4\(4n^{3}-4n^{2}-n+4\) cho 2n+1 ta được:

4n^{3}-4n^{2}-n+4=(2n+1)(n^{2}+1)+3\(4n^{3}-4n^{2}-n+4=(2n+1)(n^{2}+1)+3\)

Từ đó suy ra, để có phép chia hết điều kiện là 3 chia hết cho 2n+1, tức là cần tìm giá trị nguyên của n để 2n+1 là ước của 3, ta được:

2n+1=3\Leftrightarrow n=1\(2n+1=3\Leftrightarrow n=1\)

2n+1=1\Leftrightarrow n=0\(2n+1=1\Leftrightarrow n=0\)

2n+1=-3\Leftrightarrow n=-2\(2n+1=-3\Leftrightarrow n=-2\)

2n+1=-1\Leftrightarrow n=-1\(2n+1=-1\Leftrightarrow n=-1\)

Vây n = 1;n = 0; n = 2 thỏa mãn điều kiện đề bài.

Ứng dụng định lý Bezout khi giải

Ngoài ra còn có các dạng toán liên quan như: chia đa thức chứa tham số; chia đa thức với đa thức nguyên hàm.

IV. Bài tập chia đa thức cho đa thức lớp 8

A. Tự luận

Bài 1: Tính nhanh:

1. (4x^{2}-9y^{2}) : (2x-3y)\((4x^{2}-9y^{2}) : (2x-3y)\)

2. (27x^{3}-1) : (3x-1)\((27x^{3}-1) : (3x-1)\)

3. (8x^{3}+1) : (4x^{2}-2x+1)\((8x^{3}+1) : (4x^{2}-2x+1)\)

4. (x^{2}- 3x + xy -3y) : (x + y)\((x^{2}- 3x + xy -3y) : (x + y)\)

Giải

1. (4x^{2}-9y^{2}) : (2x-3y) = [(2x)^{2}–(3y)^{2}] : (2x-3y)=2x+3y\((4x^{2}-9y^{2}) : (2x-3y) = [(2x)^{2}–(3y)^{2}] : (2x-3y)=2x+3y\)

2. (27x^{3}-1) : (3x-1) = [(3x)^{3}-1] : (3x-1) = (3x)^{2} + 3x + 1 = 9x^{2} + 3x + 1\((27x^{3}-1) : (3x-1) = [(3x)^{3}-1] : (3x-1) = (3x)^{2} + 3x + 1 = 9x^{2} + 3x + 1\)

3.(8x^{3}+1):(4x^{2}–2x+1)=[(2x)^{3}+1]:(4x^{2}-2x+1)\((8x^{3}+1):(4x^{2}–2x+1)=[(2x)^{3}+1]:(4x^{2}-2x+1)\)

=(2x+1)[(2x)^{2}–2x+1]:(4x^{2}–2x+1)\(=(2x+1)[(2x)^{2}–2x+1]:(4x^{2}–2x+1)\)

=( 2x+1)(4x^{2}–2x+1):(4x^{2}–2x+1)=2x+1\(=( 2x+1)(4x^{2}–2x+1):(4x^{2}–2x+1)=2x+1\)

4. (x^{2}-3x + xy -3y) : (x + y) = [(x^{2}+ xy)-(3x+3y)] : (x + y)\((x^{2}-3x + xy -3y) : (x + y) = [(x^{2}+ xy)-(3x+3y)] : (x + y)\)

= [x(x + y)-3(x + y)] : (x + y)\(= [x(x + y)-3(x + y)] : (x + y)\)

= (x + y) (x-3) : (x + y) = x-3\(= (x + y) (x-3) : (x + y) = x-3\)

Bài 2: Thực hiện phép chia:

a) \left(-3 x^{3}+5 x^{2}-9 x+15\right):(-3 x+5)\(\left(-3 x^{3}+5 x^{2}-9 x+15\right):(-3 x+5)\)

b) \left(5 x^{4}+9 x^{3}-2 x^{2}-4 x-8\right):(x-1)\(\left(5 x^{4}+9 x^{3}-2 x^{2}-4 x-8\right):(x-1)\)

c) \left(5 x^{3}+14 x^{2}+12 x+8\right):(x+2);\(\left(5 x^{3}+14 x^{2}+12 x+8\right):(x+2);\)

d) \left(x^{4}-2 x^{3}+2 x-1\right):\left(x^{2}-1\right).\(\left(x^{4}-2 x^{3}+2 x-1\right):\left(x^{2}-1\right).\)

Bài 3: Làm phép chia bằng cách áp dụng hằng đẳng thức:

a) \left(x^{8}-2 x^{4} y^{4}+y^{8}\right):\left(x^{2}+y^{2}\right)\(\left(x^{8}-2 x^{4} y^{4}+y^{8}\right):\left(x^{2}+y^{2}\right)\)

b) \left(64 x^{3}+27\right):\left(16 x^{2}-12 x+9\right)\(\left(64 x^{3}+27\right):\left(16 x^{2}-12 x+9\right)\)

c) \left(x^{3}-9 x^{2}+27 x-27\right):\left(x^{2}-6 x+9\right)\(\left(x^{3}-9 x^{2}+27 x-27\right):\left(x^{2}-6 x+9\right)\)

d) \left(x^{3} y^{6} z^{9}-1\right):\left(x y^{2} z^{3}-1\right).\(\left(x^{3} y^{6} z^{9}-1\right):\left(x y^{2} z^{3}-1\right).\)

Bài 4: Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi làm phép chia:

a) \left(13 x+41 x^{2}+35 x^{3}-14\right):(5 x-2) ;\(\left(13 x+41 x^{2}+35 x^{3}-14\right):(5 x-2) ;\)

b) \left(16 x^{2}-22 x+15-6 x^{3}+x^{4}\right):\left(x^{2}-2 x+3\right)\(\left(16 x^{2}-22 x+15-6 x^{3}+x^{4}\right):\left(x^{2}-2 x+3\right)\)

c)\left(6 x+2 x^{3}-5-11 x^{2}\right):\left(-x+2 x^{2}+1\right).\(\left(6 x+2 x^{3}-5-11 x^{2}\right):\left(-x+2 x^{2}+1\right).\)

Bài 5: Tìm m đề đa thức 3 x^{3}+2 x^{2}-7 x+m\(3 x^{3}+2 x^{2}-7 x+m\) chia hết cho đa thức 3x-1

Bài 6 Tìm số dư trong phép chia đa thức f(y)=y^{243}+y^{81}+y^{27}+y^{9}+y^{3}+y\(f(y)=y^{243}+y^{81}+y^{27}+y^{9}+y^{3}+y\) cho đa thứcg(y)=y^{2}-1\(g(y)=y^{2}-1\)

Bài 7: Phân tích các đa thức sau thành nhân tử:

a, {x^3} - 4{x^2} + x + 6\({x^3} - 4{x^2} + x + 6\)

b, {x^3} - 5{x^2} - 2x + 24\({x^3} - 5{x^2} - 2x + 24\)

c, 2{x^4} - {x^3} - 17{x^2} + x + 15\(2{x^4} - {x^3} - 17{x^2} + x + 15\)

d, 3{x^4} + 5{x^3} - 5{x^2} - 5x + 2\(3{x^4} + 5{x^3} - 5{x^2} - 5x + 2\)

Bài 8: Thực hiện phép chia đa thức:

a, {x^5} + 6{x^4} + 3{x^2} - 2x - 10\({x^5} + 6{x^4} + 3{x^2} - 2x - 10\) cho x + 8\(x + 8\)

b, 2{x^7} - 8{x^5} + 3{x^3} - 9{x^2} - 10x + 1\(2{x^7} - 8{x^5} + 3{x^3} - 9{x^2} - 10x + 1\) cho x - 5\(x - 5\)

c, {x^4} + 12{x^2} - 25\({x^4} + 12{x^2} - 25\) cho 2x + 5\(2x + 5\)

d, {x^5} - 7{x^4} + 8{x^3} - 4{x^2} - 10x + 13\({x^5} - 7{x^4} + 8{x^3} - 4{x^2} - 10x + 13\) cho x + 1\(x + 1\)

Bài 9: Giải các phương trình sau:

a, 2{x^4} - 5{x^3} + 6{x^2} - 5x + 2 = 0\(2{x^4} - 5{x^3} + 6{x^2} - 5x + 2 = 0\)

b, \left( {x + 2} \right)\left( {x - 3} \right)\left( {x + 4} \right)\left( {x - 6} \right) + 6{x^2} = 0\(\left( {x + 2} \right)\left( {x - 3} \right)\left( {x + 4} \right)\left( {x - 6} \right) + 6{x^2} = 0\)

c, \left( {{x^2} + x + 2} \right)\left( {{x^2} + x + 3} \right) = 6\(\left( {{x^2} + x + 2} \right)\left( {{x^2} + x + 3} \right) = 6\)

d, 2{x^4} - 21{x^3} + 34{x^2} + 105x + 50 = 0\(2{x^4} - 21{x^3} + 34{x^2} + 105x + 50 = 0\)

B. Trắc nghiệm 

Bài 1: Kết quả của phép chia ( 7x3 - 7x + 42 ):( x2 - 2x + 3 ) là ?

A. - 7x + 14 B. 7x + 14C. 7x - 14 D. - 7x - 14

Bài 2: Phép chia x3 + x2 - 4x + 7 cho x2 - 2x + 5 được đa thức dư là ?

A. 3x - 7. B. - 3x - 8.C. - 15x + 7. D. - 3x - 7.

Bài 3: Hệ số a thỏa mãn để 4x2 - 6x + a chia hết có x - 3 là ?

A. a = - 18. B. a = 8.C. a = 18. D. a = - 8.

Bài 4: Thực hiện phép chia: (4x4 + x + 2x3 - 3x2) : (x2 + 1) ta được số dư là :

A. – x + 7B. 4x2 + 2x - 7C. 4x2 – 2x + 7D. x – 7

Bài 5: Thực hiện phép chia (3x3 + 2x + 1 ) : (x + 2) ta được đa thức dư là :

A. 10 B. -9C. – 15 D. – 27

Bài 6: Thực hiện phép chia (-4x4 + 5x2 + x ) : (x2 + x) ta được kết quả là:

A. – 4x4 + 5x2 + x = (x2 + x).(-4x2 - 4x + 9) - 6xB. – 4x4 + 5x2 + x = (x2 + x).(4x2 + 4x + 9) + 12xC. – 4x4 + 5x2 + x = (x2 + x).(-4x2 + 4x + 9) - 8xD. – 4x4 + 5x2 + x = (x2 + x). ( 4x2 - 4x + 9) + 10x

Bài 7: Cho phép chia: (x3 + 9x2 + 27x + 27) : (x + 3). Tìm khẳng định sai?

A. Đây là phép chia hếtB. Thương của phép chia là: (x + 3)2C. Thương của phép chia là: x2 + 6x + 9D. Số dư của phép chia là: x – 3 .

Bài 8: Thực hiện phép chia: (x2y + 4xy + 3y ) : (x + 1) ta được thuơng là:

A. xy + 3 B. x + 3yC. x + y + 3 D. y. (x + 3)

Bài 9: Tìm a để phép chia (x3 – 4x + a): (x – 2) là phép chia hết:

A. a = 0 B. a = 4C. a = -8D. a = 8

Bài 10: Kết quả của phép chia (2a3 + 7ab2 – 7a2 – 2b3) : (2a – b) là

A. (a – b)(a – 2b)B. (a + b)2C. (a – b)(b – 2a)D. a – b

Lời giải

Ta có 2a3 + 7ab2 – 7a2 – 2b3

= 2(a3 – b3) – 7ab(a – b)

= 2(a – b)(a2 + ab + b2) – 7ab(a – b)

= (a – b)(2a2 – ab – 4ab + 2b2)

= (a – b)[a(2a – b) – 2b(2a – b)]

= (a – b)(2a – b)(a – 2b)

Nên (2a3 + 7ab2 – 7a2 – 2b3) : (2a – b)

= (a – b)(2a – b)(a – 2b) : (2a – b) = (a – b)(a – 2b)

Đáp án cần chọn là: A

Bài 11: Kết quả của phép chia (x4 – x3y + x2y2 – xy3) : (x2 + y2) là

A. (x – y)B. x(x – y)C. x2 – yD. x2 + xy

Lời giải

Ta có x4 – x3y + x2y2 – xy3

= x4 + x2y2 – (x3y + xy3)

= x2(x2 + y2) – xy(x2 + y2)

= (x2 + y2)(x2 – xy) = (x2 + y2)x(x – y)

Nên (x4 – x3y + x2y2 – xy3) : (x2 + y2)

= (x2 + y2)x(x – y) : (x2 + y2) = x(x – y)

Đáp án cần chọn là : B

Bài 12: Xác định a để đa thức 27x2 + a chia hết cho 3x + 2

A. x = 6B. a = 12C. a = -12D. a = 9

Lời giải: Đáp án C

Bài 13: Xác định a để đa thức 10x2 – 7x + a chia hết cho 2x – 3

A. a = 24B. a = 12C. a = -12D. a = 9

Lời giải: Đáp án C

Từ khóa » Cách Chia đa Thức Cho đa Thức Có Dư