Cho Dãy Số (un), Biết U1= 2, Un 1= \(\dfrac{2017 U_n}{2019 ... - Olm

Học liệu Hỏi đáp Đăng nhập Đăng ký

• Học bài
• Hỏi bài
• Kiểm tra
• ĐGNL
• Thi đấu
• Thư viện số
• Bài viết Cuộc thi Tin tức Blog học tập
• Trợ giúp
• Về OLM

(Từ ngày 12/12) Lớp live ôn thi cuối kỳ I hoàn toàn miễn phí - Tham gia ngay!!!

 Mở bộ đề mới - nhận quà VIP liền tay

• Mẫu giáo
• Lớp 1
• Lớp 2
• Lớp 3
• Lớp 4
• Lớp 5
• Lớp 6
• Lớp 7
• Lớp 8
• Lớp 9
• Lớp 10
• Lớp 11
• Lớp 12
• ĐH - CĐ

K Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xác nhận câu hỏi phù hợp

×

Chọn môn học Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên Mua vip

• Tất cả
• Mới nhất
• Câu hỏi hay
• Chưa trả lời
• Câu hỏi vip

MN Minh Nguyệt 29 tháng 3 2021

Cho dãy số (un), biết u1= 2, un+1= \(\dfrac{2017+u_n}{2019-u_n},n\ge1\) . Xác định công thức số hạng tổng quát un và tìm limun

#Hỏi cộng đồng OLM #Toán lớp 11 1 NV Nguyễn Việt Lâm 29 tháng 3 2021

Đặt \(u_n=v_n+1\Rightarrow v_{n+1}+1=\dfrac{2017+v_n+1}{2019-\left(v_n+1\right)}=\dfrac{2018+v_n}{2018-v_n}\)

\(\Rightarrow v_{n+1}=\dfrac{2018+v_n}{2018-v_n}-1=\dfrac{2v_n}{2018-v_n}\Rightarrow\dfrac{1}{v_{n+1}}=1009\dfrac{1}{v_n}-\dfrac{1}{2}\)

Đặt \(\dfrac{1}{v_n}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{1}{v_1}=\dfrac{1}{u_1-1}=1\\x_{n+1}=1009x_n-\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow x_{n+1}-\dfrac{1}{2016}=1009\left(x_n-\dfrac{1}{2016}\right)\)

\(\Rightarrow x_n-\dfrac{1}{2016}\) là CSN với công bội 1009 \(\Rightarrow x_n-\dfrac{1}{2016}=\dfrac{2015}{2016}.1009^{n-1}\)

\(\Rightarrow x_n=\dfrac{2015}{2016}1009^{n-1}+\dfrac{1}{2016}\) 

\(\Rightarrow u_n=v_n+1=\dfrac{1}{x_n}+1=\dfrac{2016}{2015.1009^{n-1}+1}+1\)

\(\Rightarrow\lim\left(u_n\right)=1\)

Đúng(2) TT Trần Thanh Phương 29 tháng 3 2021

Có thể đặt \(u_n=v_n+2017\) nữa bác nhỉ, bác có công thức tổng quát tìm t không ạ: \(u_n=v_n+t\).

Đúng(0) Những câu hỏi liên quan TP Trinh Phương 8 tháng 2 2022 Cho dãy số (un) thỏa mãn u1 = \(\dfrac{2}{3}\) và un+1 = \(\dfrac{u_n}{2\left(2n+1\right)u_n+1}\left(n\ge1\right)\). Tìm số hạng tổng quát un của dãy. Tính lim...Đọc tiếp

Cho dãy số (un) thỏa mãn u1 = \(\dfrac{2}{3}\) và un+1 = \(\dfrac{u_n}{2\left(2n+1\right)u_n+1}\left(n\ge1\right)\). Tìm số hạng tổng quát un của dãy. Tính lim un

#Hỏi cộng đồng OLM #Toán lớp 11 1 C ☆Châuuu~~~(๑╹ω╹๑ )☆ 8 tháng 2 2022

Đúng(3) GN GV Nguyễn Trần Thành Đạt Giáo viên 8 tháng 2 2022

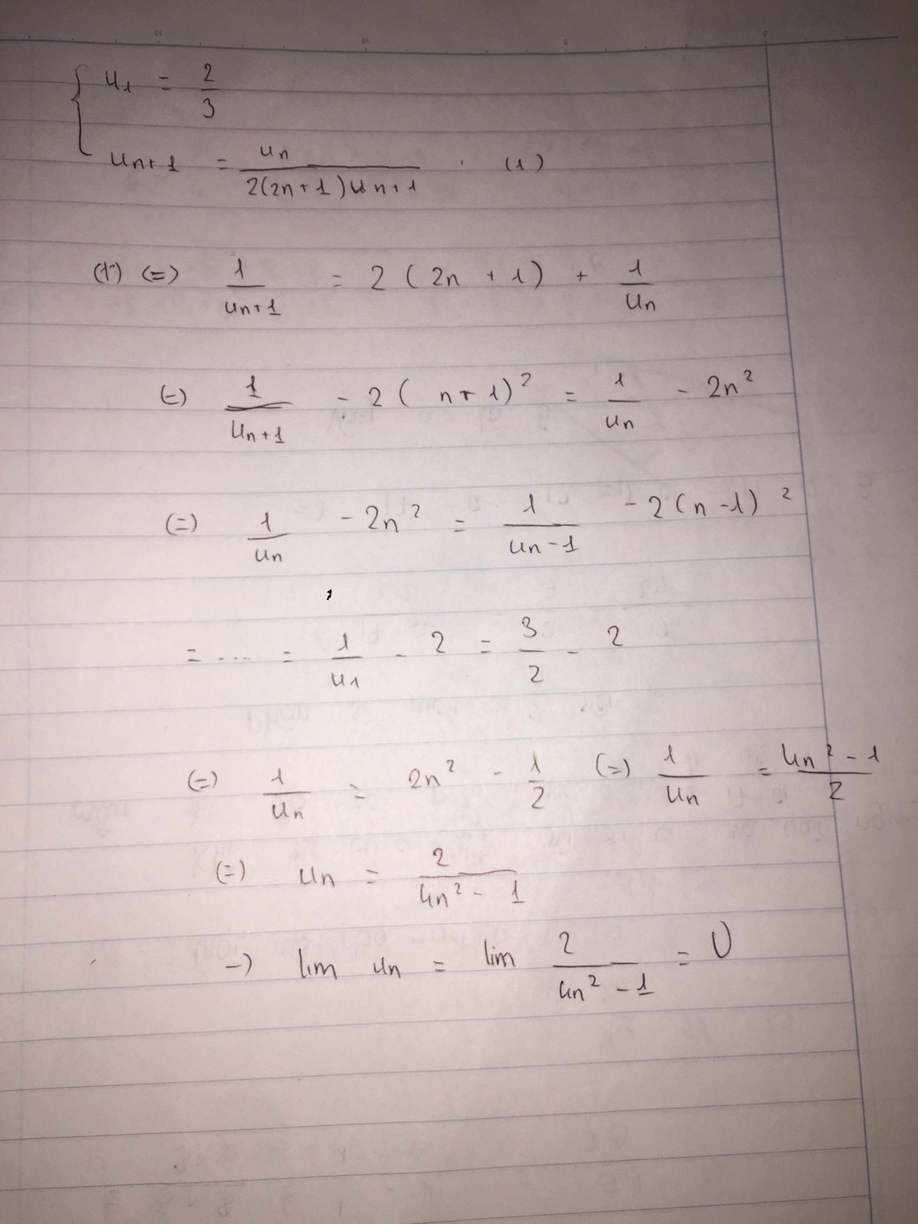
Ủa lớp 9 học lim rồi á?

Đúng(0) KH Kimian Hajan Ruventaren 22 tháng 12 2021

Cho dãy số (un) biết u1 = 3; \(u_{n+1}=\sqrt{1+u_n^2}\) với \(n\ge1\). Tìm công thức của số hạng tổng quát un

 

#Hỏi cộng đồng OLM #Toán lớp 11 1 LT Lê Thị Thục Hiền 23 tháng 12 2021

\(u_{n+1}=\sqrt{1+u_n^2}\left(1\right)\)

\(u_1=3=\sqrt{9}\)

\(u_2=\sqrt{1+u_1^2}=\sqrt{10}\)

\(u_3=\sqrt{1+u_2^2}=\sqrt{11}\)

...

Dự đoán công thức:\(u_n=\sqrt{n+8}\),\(n\ge1\) (*)

Thật vậy 

+)\(n=1,(*)\)\(\Leftrightarrow u_1=3\) (lđ)

+)Giả sử (*) đúng với mọi \(n=k,k>1\)

\((*)\Leftrightarrow u_k=\sqrt{k+8}\)

+)\(n=k+1,\) thay vào (1) có: \(u_{k+2}=\sqrt{1+u^2_{k+1}}=\sqrt{1+\left(\sqrt{1+u_k^2}\right)^2}=\sqrt{2+u^2_k}=\sqrt{2+k+8}=\sqrt{10+k}\)

\(\Rightarrow\)(*) đúng với n=k+1

Vậy CTSHTQ: \(u_n=\sqrt{n+8}\), \(n\ge1\)

Đúng(0) LT Lê Thu Hiền 9 tháng 8 2021

Cho dãy số (un) xác định bởi :  u1=1 ,\(u_{n+1}=\dfrac{3}{2}\left(u_n-\dfrac{n+4}{n^2+3n+2}\right)\) 

Tìm công thức số hạng tổng quát un   theo n

#Hỏi cộng đồng OLM #Toán lớp 11 1 NV Nguyễn Việt Lâm 9 tháng 8 2021

\(u_{n+1}=\dfrac{3}{2}\left(u_n-\dfrac{n+4}{\left(n+1\right)\left(n+2\right)}\right)=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}+\dfrac{2}{n+2}\right)\)

\(\Leftrightarrow u_{n+1}-\dfrac{3}{n+1+1}=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}\right)\)

Đặt \(u_n-\dfrac{3}{n+1}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-\dfrac{3}{2}=-\dfrac{1}{2}\\v_{n+1}=\dfrac{3}{2}v_n\end{matrix}\right.\)

\(\Rightarrow v_n\) là CSN với công bội \(\dfrac{3}{2}\)

\(\Rightarrow v_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}\)

\(\Rightarrow u_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}+\dfrac{3}{n+1}\)

Đúng(2) BC Big City Boy 4 tháng 12 2023

Cho dãy số (Un) xác định bởi:\(\left\{{}\begin{matrix}u_1=1\\u_{n+1}=-\dfrac{3}{2}u_n^2+\dfrac{5}{2}u_n+1\end{matrix}\right.\), \(\forall n\ge1\)

1) Hãy tính u2.u3,u4,u5

2) Dự đoán công thức của số hạng tổng quát Un

#Hỏi cộng đồng OLM #Toán lớp 11 0 NN Ngọc Nhã Uyên Hạ 19 tháng 1 2021 Cho dãy số (Un) được xác định bởi: u1 = \(\dfrac{1}{3}\) và un+1 = \(\dfrac{2u_n}{2u_n\left(3n-1\right)+1}\), ∀n ∈ N*.a) Tìm u4 và số hạng tổng quát un của dãy số.b) Tính S = \(\dfrac{1}{u_1}+\dfrac{1}{u_2}+...+\dfrac{1}{u_n}\) (tổng gồm n số hạng) theo n.Help me!!!Gấp lắm ạThank you so...Đọc tiếp

Cho dãy số (Un) được xác định bởi: u1 = \(\dfrac{1}{3}\) và un+1 = \(\dfrac{2u_n}{2u_n\left(3n-1\right)+1}\), ∀n ∈ N*.

a) Tìm u4 và số hạng tổng quát un của dãy số.

b) Tính S = \(\dfrac{1}{u_1}+\dfrac{1}{u_2}+...+\dfrac{1}{u_n}\) (tổng gồm n số hạng) theo n.

Help me!!!

Gấp lắm ạ

Thank you so much!!!

#Hỏi cộng đồng OLM #Toán lớp 11 0 BC Big City Boy 27 tháng 11 2023

Cho dãy số (Un) xác định bởi công thức truy hồi \(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\dfrac{n+2}{4.\left(n+1\right)}u_n\end{matrix}\right.\), \(n\in\)N*. Công thức số hạng tổng quát của dãy số (Un) là?

#Hỏi cộng đồng OLM #Toán lớp 11 1 TC Trên con đường thành công không có.... 27 tháng 11 2023

Đặt \(\dfrac{u_n}{n+1}=v_n\)

\(GT\Rightarrow\left\{{}\begin{matrix}v_1=\dfrac{u_1}{1+1}=1\\v_{n+1}=\dfrac{1}{4}v_n,\forall n\in N\text{*}\end{matrix}\right.\)

\(\Rightarrow v_n=\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)

\(\Rightarrow u_n=\left(n+1\right).\dfrac{1}{4}^{n-1},\forall n\in N\text{*}\)

Đúng(3) VP Việt Phương 17 tháng 2 2021

cho dãy số(un) được xác định bởi \(\left\{{}\begin{matrix}u_1=2\\u_{n+1}=\sqrt{\dfrac{n+1}{n}}\left(u_n+3\right)-3\end{matrix}\right.\)    ,n=1,2,...Tìm công thức tổng quát của dãy số (un) và tính \(\lim\limits\dfrac{u_n}{\sqrt{n}}\) .

#Hỏi cộng đồng OLM #Toán lớp 11 1 HT Hoàng Tử Hà 18 tháng 2 2021

\(u_2=\sqrt{2}\left(2+3\right)-3=5\sqrt{2}-3\)

\(u_3=\sqrt{\dfrac{3}{2}}.5\sqrt{2}-3=5\sqrt{3}-3\)

\(u_4=\sqrt{\dfrac{4}{3}}.5\sqrt{3}-3=5\sqrt{4}-3\)

....

\(\Rightarrow u_n=5\sqrt{n}-3\)

\(\Rightarrow\lim\limits\dfrac{u_n}{\sqrt{n}}=\lim\limits\dfrac{5\sqrt{n}-3}{\sqrt{n}}=5\)

Đúng(0) BC Big City Boy 23 tháng 12 2023

Cho dãy số (Un) xác định bởi công thức: \(\left\{{}\begin{matrix}u_1=2021\\u_{n+1}=\left[1-\dfrac{1}{\left(n+1\right)^2}\right]u_n+\dfrac{2020}{\left(n+1\right)^2};\forall n\ge1\end{matrix}\right.\). Khi đó limUn bằng?

#Hỏi cộng đồng OLM #Toán lớp 11 2 TC Trên con đường thành công không có.... 23 tháng 12 2023

Ta có: \(u_n>2020\) với mọi \(n\in N\text{*}\) \(\left(\text{*}\right)\)

Thật vậy, dễ thấy \(u_1=2021>2020\)

Giả sử \(\left(\text{*}\right)\) đúng với \(n=k\left(k\ge1\right)\)

\(\Rightarrow u_k>2020\)\(\Rightarrow u_{k+1}=\left[1-\dfrac{1}{\left(k+1\right)^2}\right]u_k+\dfrac{2020}{\left(k+1\right)^2}\)

\(>\left[1-\dfrac{1}{\left(k+1\right)^2}\right].2020+\dfrac{2020}{\left(k+1\right)^2}=2020\)

\(\Rightarrow\left(\text{*}\right)\) đúng với \(n=k+1\)

Do đó theo nguyên lý quy nạp ta có đpcm.

Lại có:

\(u_{n+1}-u_n=\dfrac{2020}{\left(n+1\right)^2}-\dfrac{u_n}{\left(n+1\right)^2}< 0\) với mọi \(n\in N\text{*}\)

\(\Rightarrow\left(u_n\right)\) là dãy giảm

\(\left(u_n\right)\) là dãy giảm và bị chặn nên \(\left(u_n\right)\) là dãy hội tụ

Đặt \(limu_n=L\)

\(\Rightarrow\left\{{}\begin{matrix}2020\le L\le2021\\L=\left[1-\dfrac{1}{\left(n+1\right)^2}\right].L+\dfrac{2020}{\left(n+1\right)^2}\end{matrix}\right.\)\(\Rightarrow L=2020\left(tm\right)\)

Vậy \(limu_n=2020\)

 

Đúng(1) TC Trên con đường thành công không có.... 23 tháng 12 2023

Ta có: \(u_n>2020\) với mọi \(n\in N\text{*}\) \(\left(\text{*}\right)\)

Thật vậy, dễ thấy \(u_1=2021>2020\)

Giả sử \(\left(\text{*}\right)\) đúng với \(n=k\left(k\ge1\right)\)

\(\Rightarrow u_k>2020\)\(\Rightarrow u_{k+1}=\left[1-\dfrac{1}{\left(k+1\right)^2}\right]u_k+\dfrac{2020}{\left(k+1\right)^2}\)

\(>\left[1-\dfrac{1}{\left(k+1\right)^2}\right].2020+\dfrac{2020}{\left(k+1\right)^2}=2020\)

\(\Rightarrow\left(\text{*}\right)\) đúng với \(n=k+1\)

Do đó theo nguyên lý quy nạp ta có đpcm.

Lại có:

\(u_{n+1}-u_n=\dfrac{2020}{\left(n+1\right)^2}-\dfrac{u_n}{\left(n+1\right)^2}< 0\) với mọi \(n\in N\text{*}\)

\(\Rightarrow\left(u_n\right)\) là dãy giảm

\(\left(u_n\right)\) là dãy giảm và bị chặn nên \(\left(u_n\right)\) là dãy hội tụ

Đặt \(limu_n=L\)

\(\Rightarrow\left\{{}\begin{matrix}2020\le L\le2021\\L=\left[1-\dfrac{1}{\left(n+1\right)^2}\right].L+\dfrac{2020}{\left(n+1\right)^2}\end{matrix}\right.\)\(\Rightarrow L=2020\left(tm\right)\)

Vậy \(limu_n=2020\)

 

Đúng(1) Xem thêm câu trả lời T títtt 30 tháng 8 2023 1) cho dãy số un=\(n^2-1\)�=3�−1a) Tính b) 99 là số hạng thứ mấy của dãy2) cho dãy số \(u_n=\dfrac{2n-1}{n+1}\)u1,u2,u3,u4b) \(\dfrac{13}{7}\) là số hạng thứ mấy của...Đọc tiếp

1) cho dãy số un=\(n^2-1\)�=3�−1

a) Tính b) 99 là số hạng thứ mấy của dãy

2) cho dãy số \(u_n=\dfrac{2n-1}{n+1}\)

u1,u2,u3,u4

b) \(\dfrac{13}{7}\) là số hạng thứ mấy của dãy #Hỏi cộng đồng OLM #Toán lớp 11 2 M meme 30 tháng 8 2023

a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = n^2 - 1:

u1 = 1^2 - 1 = 0 u2 = 2^2 - 1 = 3 u3 = 3^2 - 1 = 8 u4 = 4^2 - 1 = 15

Vậy u1 = 0, u2 = 3, u3 = 8, u4 = 15.

b) Để tìm số hạng thứ mấy trong dãy có giá trị 99, ta giải phương trình n^2 - 1 = 99:

n^2 - 1 = 99 n^2 = 100 n = 10 hoặc n = -10

Vì số hạng của dãy phải là số tự nhiên nên ta chọn n = 10. Vậy số hạng thứ mấy có giá trị 99 là u10.

a) Để tính các số hạng u1, u2, u3, u4 của dãy (un), ta thay n = 1, 2, 3, 4 vào công thức un = (2n - 1)/(n + 1):

u1 = (21 - 1)/(1 + 1) = 1/2 u2 = (22 - 1)/(2 + 1) = 3/3 = 1 u3 = (23 - 1)/(3 + 1) = 5/4 u4 = (24 - 1)/(4 + 1) = 7/5

Vậy u1 = 1/2, u2 = 1, u3 = 5/4, u4 = 7/5.

b) Để tìm số hạng thứ mấy trong dãy có giá trị 137137, ta giải phương trình (2n - 1)/(n + 1) = 137137:

(2n - 1)/(n + 1) = 137137 2n - 1 = 137137(n + 1) 2n - 1 = 137137n + 137137 137135n = 137138 n = 1

Vậy số hạng thứ mấy có giá trị 137137 là u1.

Đúng(0) NL Nguyễn Lê Phước Thịnh 30 tháng 8 2023

Đúng(0) Xem thêm câu trả lời Xếp hạng Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên

• Tuần
• Tháng
• Năm

• E ✦𝘉é✿𝘤𝘩í𝘱✦ 2 GP
• E ElmSunn 2 GP
• NT Nguyễn Trọng Đạt VIP 2 GP
• -❇️🆗𝕰𝔛𝕻𝔈𝕽ℑ𝕰𝔑𝕮𝔈𝕯✳️𝕻𝔈𝕺𝔓𝕷𝔈🆒❎- 2 GP
• D Đ𝙖̆𝙣𝙜 𝙈𝙞𝙣𝙝 (𝙈𝙚𝙤𝙠𝙤𝙣𝙝𝙤𝙣𝙜𝙪𝙤𝙣𝙜𝙩𝙝𝙪𝙤𝙘) 2 GP
• NV ✫⊰ Ngô Vũ ༒ Công Vinh ⊱✫ VIP 2 GP
• NT Nguyễn Thanh Trúc 2 GP
• LD Lê Duy Anh 2 GP
• NB Nguyễn Bá Hiếu 2 GP
• ND Nguyễn Đỗ Bảo Hân 2 GP

Học liệu Hỏi đáp Link rút gọn Link rút gọn Để sau Đăng ký

Các khóa học có thể bạn quan tâm

× Mua khóa học Tổng thanh toán: 0đ (Tiết kiệm: 0đ) Tới giỏ hàng Đóng ×

Yêu cầu VIP

×

Học liệu này đang bị hạn chế, chỉ dành cho tài khoản VIP cá nhân, vui lòng nhấn vào đây để nâng cấp tài khoản.