Cho Hình Chóp S.ABCD Có đáy ABCD Là Hình Thang ...

Có thể bạn quan tâm

Đăng nhập Facebook

Google

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 12 Toán

Câu hỏi:

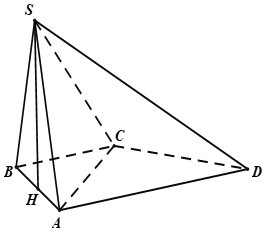
21/07/2024 7,412

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = 12AD = a. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ACD.

A. V=a33

B. V=a32

C. V=a326

D. V=a336

Đáp án chính xác Xem lời giải Xem lý thuyết Câu hỏi trong đề: 80 câu trắc nghiệm: Thể tích khối đa diện (có đáp án) Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Câu trả lời này có hữu ích không?

3 2

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

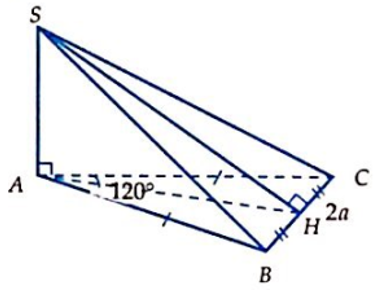
Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a,BAC^= 120°, biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC.

Xem đáp án » 13/02/2022 7,464

Câu 2:

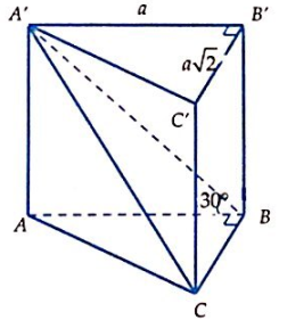
Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B; AB = a, BC=a2 $\sqrt{2}$ ; mặt phẳng (A'BC) hợp với mặt đáy (ABC) góc 30°. Thể tích của khối lăng trụ là:

Xem đáp án » 13/02/2022 6,612

Câu 3:

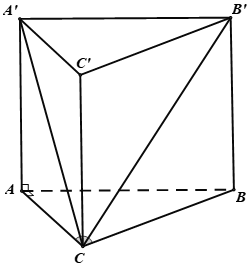
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC = a, $\hat{ACB}$ = 60°. Đường chéo B’C tạo với mặt phẳng (AA’C’C) một góc 30°. Tính thể tích của khối lăng trụ theo a.

Xem đáp án » 15/02/2022 5,895

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 120°, SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng

Xem đáp án » 13/02/2022 3,937

Câu 5:

Cho hình lăng trụ ABC.A’B’C’, đáy ABC có AC = a3; BC = 3a, $\hat{A C B}$ = 30°. Cạnh bên hợp với mặt phẳng đáy góc 60° và mặt phẳng (A’BC) vuông góc với mặt phẳng (ABC). Điểm H trên cạnh BC sao cho BC = 3BH và mặt phẳng (A’AH) vuông góc với mặt phẳng (ABC). Thể tích khối lăng trụ ABC.A’B’C’ bằng:

Xem đáp án » 15/02/2022 3,249

Câu 6:

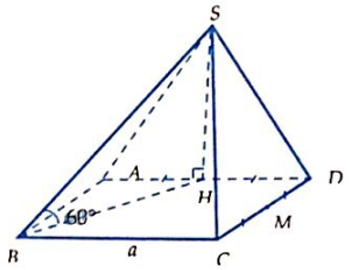
Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm của AD; M là trung điểm CD; cạnh bên SB hợp với đáy góc 60°. Thể tích của khối chóp S.ABM là:

Xem đáp án » 13/02/2022 3,179

Câu 7:

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho HC→=2BH→ $\vec{H C} = 2 \vec{B H}$ , (SAB) hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

Xem đáp án » 13/02/2022 2,681

Câu 8:

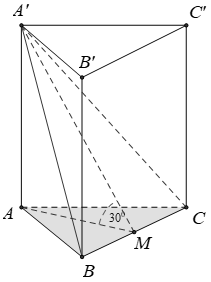
Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a và (A’BC) hợp với mặt đáy (ABC) một góc 30°. Tính thể tích hình chóp A’.ABC là

Xem đáp án » 15/02/2022 2,470

Câu 9:

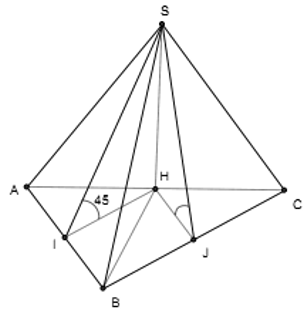
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, có BC = a. Mặt bên SAC vuông góc với đáy các mặt bên còn lại đều tạo với mặt đáy một góc 45°. Thể tích khối chóp S.ABC bằng

Xem đáp án » 13/02/2022 2,238

Câu 10:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), SAB^=30o, SA = 2a. Tính thể tích V của khối chóp S.ABCD.

Xem đáp án » 13/02/2022 2,217

Câu 11:

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng (AB’C’) tạo với mặt đáy góc 60°. Tính theo a thể tích lăng trụ ABC.A’B’C’.

Xem đáp án » 15/02/2022 2,177

Câu 12:

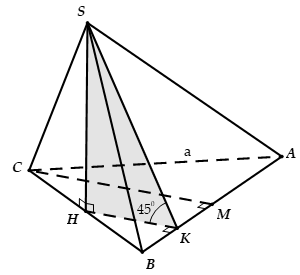
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm của BC và (SAB) hợp với đáy một góc 45°. Tính thể tích V của khối chóp S.ABC

Xem đáp án » 13/02/2022 2,072

Câu 13:

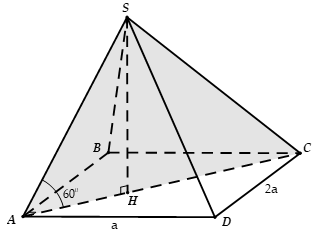
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, BC = 2AB = 2a tam giác SAC nằm trong mặt phẳng vuông góc với (ABCD),SAC^= 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD

Xem đáp án » 13/02/2022 1,993

Câu 14:

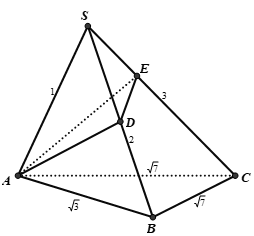
Cho hình chóp S.ABC có các cạnh SA = 1, SB = 2, SC = 3, AB=3, BC=CA=7 .Tính thể tích V khối chóp S.ABC.

Xem đáp án » 13/02/2022 1,937

Câu 15:

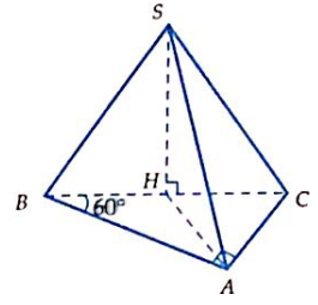
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, ABC^ $\hat{A B C}$ = 60°. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Góc giữa SA và mặt phẳng đáy bằng 45°. Tính thể tích khối chóp S.ABC.

Xem đáp án » 13/02/2022 1,731 Xem thêm các câu hỏi khác »

LÝ THUYẾT

Mục lục nội dung

Xem thêm

I. Khái niệm về thể tích của khối đa diện

Người ta chứng minh được rằng: có thể đặt tương ứng cho mỗi khối đa diện (H) một số dương duy nhất V(H) thỏa mãn các tính chất sau:

a) Nếu (H) là khối lập phương có cạnh bằng 1 thì V(H) = 1.

b) Nếu hai khối đa diện (H1) và (H2) bằng nhau thì V(H1) = V(H2).

c) Nếu khối đa diện (H) được phân chia thành hai khối đa diện (H1) và (H2) thì:

V(H) = V(H1) + V(H2).

Số dương V(H) nói trên được gọi là thể tích của khối đa diện (H). Số đó cũng được gọi là thể tích của hình đa diện giới hạn khối đa diện (H).

Khối lập phương có cạnh bằng 1 được gọi là khối lập phương đơn vị.

- Định lí : Thể tích của khối hình chữ nhật bằng tích ba kích thước của nó.

II. Thể tích của khối lăng trụ.

Định lí: Thể tích khối lăng trụ có diện tích đáy B và chiều cao h là: V = B.h

Ví dụ 1. Đáy của lăng trụ đứng tam giác ABC.A’B’C’ là tam giác đều cạnh a = 4 và biết diện tích tam giác A’BC bằng 8. Tính thể tích khối lăng trụ.

Lời giải:

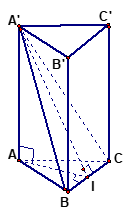
Bài 3: Khái niệm về thể tích của khối đa diện (ảnh 1)

Gọi I là trung điểm BC .

Ta có; ∆ABC đều nên

A⁢I=A⁢B⁢32= 2⁢3;A⁢I⊥B⁢C

Suy ra: A'⁢I⊥B⁢C (định lí 3 đường vuông góc)

Ta có: S=A'⁢B⁢C12BC.A'I⇒A'I=2⁢SA'⁢B⁢CB⁢C=4

Vì A⁢A'⊥(A⁢B⁢C)⇒A⁢A'⊥A⁢I

Xét tam giác A’AI có : A⁢A'=A'⁢I2-A⁢I2⁢⁢ =2

Vậy : VABC.A’B’C’ = SABC .AA' = 12⁢A⁢I.B⁢C.A⁢A'⁢=83.

III. Thể tích khối chóp.

Định lí. Thể tích khối chóp có diện tích đáy B và chiều cao h là:V=13⁢B.h.

Ví dụ 2. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a biếtSA vuông góc với đáy ABC và (SBC) hợp với đáy (ABC) một góc 60o. Tính thể tích hình chóp.

Lời giải :

Bài 3: Khái niệm về thể tích của khối đa diện (ảnh 1)

Gọi M là trung điểm của BC.

Vì tam giác ABC đều nên AM ⊥BC (định lí 3 đường vuông góc).

Vậy góc[(SBC);(ABC)] = S⁢M⁢A^= 600.

Tam giác ABC đều cạnh a nên đường cao A⁢M=a⁢32

Xét tam giác SAM có : SA = AM.tan600 = 3⁢a2

VậyV = 13⁢B.h=13⁢SA⁢B⁢C.S⁢A=13.12⁢A⁢M.B⁢C.S⁢A=a3⁢38

Đề thi liên quan

Xem thêm »

250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số 10 đề 6827 lượt thi Thi thử
Bài tập về Tính đơn điệu của hàm số có lời giải 3 đề 6471 lượt thi Thi thử
Trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số nâng cao 11 đề 5357 lượt thi Thi thử
Bài tập tắc nghiệm ứng dụng đạo hàm - Toán 12 có đáp án 7 đề 5143 lượt thi Thi thử
Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải 5 đề 3484 lượt thi Thi thử
200 câu trắc nghiệm Phương pháp tọa độ trong không gian NC (có đáp án) 9 đề 3454 lượt thi Thi thử
150 câu trắc nghiệm Nguyên hàm - Tích phân cơ bản (có đáp án) 6 đề 3283 lượt thi Thi thử
Trắc nghiệm Ôn tập Toán 12 Chương 1 có đáp án 3 đề 3023 lượt thi Thi thử
70 câu trắc nghiệm Khối đa diện cơ bản 6 đề 2982 lượt thi Thi thử
Trắc nghiệm Khái niệm về thể tích của khối đa diện có đáp án 6 đề 2782 lượt thi Thi thử

Xem thêm » Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Rô bốt có hai cái cốc loại 250 ml và 400 ml. Chỉ dùng hai cái cốc đó, làm thế nào để rô bốt lấy được 100 ml nước từ chậu nước.
207 05/04/2024 Xem đáp án
Một mảnh vườn hình vuông cạnh 20 m. Người ta làm một lối đi xung quanh vườn rộng 2 m thuộc đất của vườn. Phần đất còn lại dùng để trồng trọt. Tính diện tích trồng trọt của mảnh vườn.
116 05/04/2024 Xem đáp án
Có tất cả bao nhiêu số tự nhiên chẵn gồm 5 chữ số khác nhau được thành lập từ các chữ số 1, 2, 3, 4, 5?
121 05/04/2024 Xem đáp án
Từ các số 0; 1; 2; 7; 8; 9 tạo được bao nhiêu số lẻ có 5 chữ số khác nhau?
210 05/04/2024 Xem đáp án
Có 5 tem thư khác nhau và 6 bì thư khác nhau. Từ đó người ta muốn chọn ra 3 tem thư, 3 bì thư và dán 3 tem thư ấy lên 3 bì đã chọn. Hỏi có bao nhiêu cách làm như thế?
121 05/04/2024 Xem đáp án
Tìm m để 3 đường thẳng y = −5(x + 1), y = mx + 3, y = 3x + m phân biệt và đồng quy.
115 05/04/2024 Xem đáp án
Trung bình mỗi con gà ăn hết 102 g thức ăn trong một ngày. Hỏi trại nuôi gà đó cần bao nhiêu ki-lô-gam thức ăn cho 350 con gà trong 30 ngày?
99 05/04/2024 Xem đáp án
Cho tập hợp X gồm các số tự nhiên có 6 chữ số đôi một khác nhau có dạng $\overline {abcdef} $. Từ tập hợp X lấy ngẫu nhiên một số. Tính xác suất để số lấy ra là số lẻ và thỏa mãn a < b < c < d < e < f.
181 05/04/2024 Xem đáp án
Cho tứ diện (ABCD) có các cạnh AB, AC, AD đôi một vuông góc với nhau, AB = 6a, AC = 7a, AD = 8a.Gọi M, N, P lần lượt là trung điểm của BC, CD, BD. Tính thể tích khối tứ diện AMNP.
112 05/04/2024 Xem đáp án
Tìm tập xác định của hàm số $y = \left\{ \begin{array}{l}\sqrt {3 - x} ,x \in ( - \infty ;0)\\\sqrt {\frac{1}{x}} ,x \in (0; + \infty )\end{array} \right.$.
105 05/04/2024 Xem đáp án

Xem thêm »

Từ khóa » Hình Thang Vuông Tại A Và B

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

A. V=a33

B. V=a32

C. V=a326

D. V=a336

Trả lời:

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho khối chóp S.ABC có đáy ABC là tam giác cân tại A với BC = 2a,BAC^= 120°, biết SA ⊥ (ABC) và mặt (SBC) hợp với đáy một góc 45°. Tính thể tích khối chóp S.ABC.

Câu 2:

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B; AB = a, BC=a22; mặt phẳng (A'BC) hợp với mặt đáy (ABC) góc 30°. Thể tích của khối lăng trụ là:

Câu 3:

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC = a,ACB^= 60°. Đường chéo B’C tạo với mặt phẳng (AA’C’C) một góc 30°. Tính thể tích của khối lăng trụ theo a.

Câu 4:

Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, BAD = 120°, SA vuông góc với (ABCD). Gọi M, I lần lượt là trung điểm của BC và SB, góc giữa SM và (ABCD) bằng 60°. Khi đó thể tích của khối chóp I.ABCD bằng

Câu 5:

Câu 6:

Hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm của AD; M là trung điểm CD; cạnh bên SB hợp với đáy góc 60°. Thể tích của khối chóp S.ABM là:

Câu 7:

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho HC→=2BH→HC→=2BH→, (SAB) hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

Câu 8:

Cho hình lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a và (A’BC) hợp với mặt đáy (ABC) một góc 30°. Tính thể tích hình chóp A’.ABC là

Câu 9:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, có BC = a. Mặt bên SAC vuông góc với đáy các mặt bên còn lại đều tạo với mặt đáy một góc 45°. Thể tích khối chóp S.ABC bằng

Câu 10:

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD), SAB^=30o, SA = 2a. Tính thể tích V của khối chóp S.ABCD.

Câu 11:

Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a. Mặt phẳng (AB’C’) tạo với mặt đáy góc 60°. Tính theo a thể tích lăng trụ ABC.A’B’C’.

Câu 12:

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, hình chiếu vuông góc của S trên mặt phẳng (ABC) là trung điểm của BC và (SAB) hợp với đáy một góc 45°. Tính thể tích V của khối chóp S.ABC

Câu 13:

Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD, BC = 2AB = 2a tam giác SAC nằm trong mặt phẳng vuông góc với (ABCD),SAC^= 60°, SA = 2a. Tính thể tích V của khối chóp S.ABCD

Câu 14:

Cho hình chóp S.ABC có các cạnh SA = 1, SB = 2, SC = 3, AB=3, BC=CA=7 .Tính thể tích V khối chóp S.ABC.

Câu 15:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, ABC^ABC^ = 60°. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Góc giữa SA và mặt phẳng đáy bằng 45°. Tính thể tích khối chóp S.ABC.

LÝ THUYẾT

Đề thi liên quan

Câu hỏi mới nhất

Liên Hệ

Cho lăng trụ đứng ABC.A'B'C' có đáy ABC là tam giác vuông tại B; AB = a, BC=a2 $\sqrt{2}$ ; mặt phẳng (A'BC) hợp với mặt đáy (ABC) góc 30°. Thể tích của khối lăng trụ là:

Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông tại A, AC = a, $\hat{ACB}$ = 60°. Đường chéo B’C tạo với mặt phẳng (AA’C’C) một góc 30°. Tính thể tích của khối lăng trụ theo a.

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a hình chiếu vuông góc của S trên mặt phẳng (ABC) là điểm H trên cạnh BC sao cho HC→=2BH→ $\vec{H C} = 2 \vec{B H}$ , (SAB) hợp với đáy một góc 60°. Tính thể tích V của khối chóp S.ABC

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, cạnh AB = 2, ABC^ $\hat{A B C}$ = 60°. Hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của BC. Góc giữa SA và mặt phẳng đáy bằng 45°. Tính thể tích khối chóp S.ABC.