️ Công Thức Tính Diện Tích Hình Thoi

Hình thoi là tứ giác có bốn cạnh bằng nhau. Đây là hình bình hành có hai cạnh kề bằng nhau hay hình bình hành có hai đường chéo vuông góc với nhau.

Trong bài viết dưới đây Download.vn sẽ giới thiệu đến các bạn toàn bộ kiến thức về công thức tính diện tích hình thoi và một số bài tập kèm theo. Thông qua tài liệu này giúp các bạn học sinh có thêm nhiều tư liệu ôn tập, củng cố kiến thức làm quen với các dạng bài tập Hình học. Bên cạnh đó các bạn xem thêm công thức tính chu vi hình chữ nhật, công thức tính diện tích hình vuông.

Công thức tính diện tích hình thoi

• 1. Công thức tính diện tích hình thoi
• 2. Bài tập tính diện tích hình thoi

1. Công thức tính diện tích hình thoi

Diện tích của hình thoi bằng một nửa tích hai đường chéo của hình thoi hoặc bằng tích của chiều cao với cạnh đáy tương ứng.

a. Công thức tính diện tích hình thoi dựa đường chéo

\(S\ =\ \frac{1}{2}d_1.d_{_{2^{ }}}\)

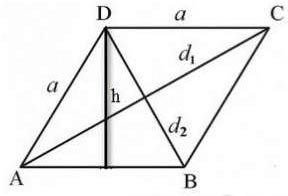
- Trong đó:

+ S: Diện tích hình thoi.

+ d1, d2: Lần lượt là kích thước 2 đường chéo của hình thoi.

+ h: Chiều cao hình thoi.

+ a: Độ dài cạnh đáy.

- Ví dụ

Tính diện tích hình thoi biết chiều dài đường chéo lần lượt là d1 = 5cm, d2 = 10cm.

Giải

S = ½ (d1 x d2) = ½ (5 x 10) = 25 cm2

b. Công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao

S = h x a.

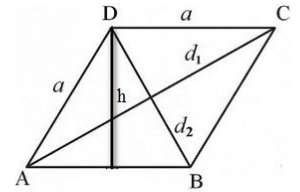
Trong đó:

- h: Chiều cao của hình thoi

- a: Cạnh đáy

c. Công thức tính diện tích hình thoi dựa vào hệ thức trong tam giác (Nếu biết góc của hình thoi)

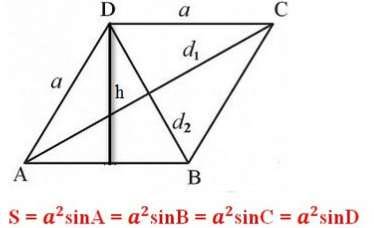
Ví dụ: Cho hình thoi ABCD, có cạnh hình thoi = 4cm, góc A = 35 độ. Tính diện tích hình thoi ABCD.

Giải: Áp dụng công thức, ta có a = 4, góc = 35 độ. Ta thay vào công thức như sau:

S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)

Lưu ý:

- Đơn vị diện tích của hình thoi là m2, cm2 ...

- Khi tính, bạn cần để ý xem đơn vị mà đề bài đưa ra đã cùng nhau chưa. Nếu chưa thì bạn cần đổi sang cùng một đơn vị trước khi làm.

2. Bài tập tính diện tích hình thoi

Bài 1: Cho hình thoi ABCD có cạnh AD = 4m, có góc DAB = 30 độ. Tính diện tích của hình thoi ABCD.

Giải:

Do ABCD là hình thoi nên các tam giác tạo thành là tam giác cân, gọi I là trung điểm hai đường chéo nên AI vuông góc với BD, góc IAB = 15 độ.

Do đó, AI = AB. cos IAB = 4.cos 15 = 3,84m.

Xét tam giác vuông ABI, theo định lý Pytago, ta có:

BI2 = AB2 - AI2 = 1,25 m.Nên BI = 1,1m

+ AC = 2. AI = 7,68 m.

+ BD = 2. BI = 2,2 m.

Do đó, diện tích của hình thoi ABCD = ½ . AC . BD = 8,45 (m2)

Bài 2: Tính diện tích hình thoi ABCD, khi biết cạnh AB = 5cm, đường chéo AC = 8cm.

Giải:

Gọi I là giao điểm của AC và BD, ta có AI = IC = 4cm

Xét tam giác vuông ABI, ta có:

BI2 = AB2 - AI2

Thay AI = 4cm, AB = 5cm, ta được: BI = 3cm

Mà BD = 2.BI = 2.3 = 6cm

Diện tích hình thoi ABCD: S = (BD . AC) : 2 = 24(cm2)