Cực Trị Của Hàm Số Là Gì? Cách Tìm Cực Trị (cực đại, Cực Tiểu) Của ...
Có thể bạn quan tâm
Bài này các em sẽ biết cực trị của hàm số là gì? hai cách (quy tắc) tìm cực trị của hàm số được thực hiện như thế nào?
• Bài tập vận dụng quy tắc tìm cực trị của hàm số
I. Khái niệm cực đại cực tiểu của hàm số
* Định nghĩa cực đại, cực tiểu
• Cho hàm số y = f(x) xác định và liên tục trên khoảng (a ; b) và điểm x0 ∈ (a ; b).
- Nếu tồn tại số h > 0 sao cho f(x) < f(x0), ∀x ∈ (x0 - h ; x0 + h), x ≠ x0 thì ta nói hàm số f đạt cực đại tại x0 .
- Nếu tồn tại số h > 0 sao cho f(x) > f(x0), ∀x ∈ (x0 - h ; x0 + h), x ≠ x0 thì ta nói hàm số f đạt cực tiểu tại x0.
> Chú ý:
- Nếu hàm số f(x) đạt cực đại (cực tiểu) tại x0 thì x0 được gọi là điểm cực đại (điểm cực tiểu) của hàm số; f(x0) được gọi là giá trị cực đại (giá trị cực tiểu) của hàm số, ký hiệu fCĐ (fCT), còn điểm M(x0; f(x0)) được gọi là điểm cực đại (điểm cực tiểu) của đồ thị.
- Các điểm cực đại và cực tiểu được gọi chung là điểm cực trị. Giá trị cực đại (giá trị cực tiểu) còn gọi là cực đại (cực tiểu) và được gọi chung là cực trị của hàm số.
- Nếu hàm số y = f(x) có đạo hàm trên khoảng (a;b) và đạt cực đại hoặc cực tiểu tại x0 thì f'(x0) = 0.
II. Điều kiện đủ để hàm số có cực trị (cực đại, cực tiểu)
• Định lý 1: Cho hàm Cho hàm số y = f(x) liên tục trên khoảng K = (x0 - h ; x0 + h) (h > 0) và có đạo hàm trên K hoặc trên K\{x0}.
- Nếu thì x0 là điểm cực đại của hàm số.
- Nếu thì x0 là điểm cực tiểu của hàm số.
Có thể hiểu đơn giản, đi từ trái qua phải:
- Nếu f'(x) đổi dấu từ - sang + khi đi qua x0 thì x0 là điểm cực tiểu.
- Nếu f'(x) đổi dấu từ + sang - khi đi qua x0 thì x0 là điểm cực đại.
• Định lý 2: Cho hàm số y = f(x) có đạo hàm cấp hai trên khoảng K = (x0 - h ; x0 + h) (h > 0).
- Nếu f'(x0) = 0, f''(x0) > 0 thì x0 là điểm cực tiểu của hàm số f.
- Nếu f'(x0) = 0, f''(x0) < 0 thì x0 là điểm cực đại của hàm số f.
III. Cách tìm cực trị của hàm số, quy tắc tìm cực trị của hàm số
• Quy tắc 1 (cách 1) để tìm cực trị của hàm số
- Tìm tập xác định.
- Tính f'(x). Tìm các điểm tại đó f'(x) bằng 0 hoặc f'(x) không xác định.
- Lập bảng biến thiên.
- Từ bảng biến thiên suy ra các điểm cực trị.
• Quy tắc 2 (cách 2) để tìm cực trị của hàm số
- Tìm tập xác định.
- Tính f'(x). Tìm các nghiệm xi của phương trình f'(x) = 0.
- Tính f''(x) và f''(xi) suy ra tính chất cực trị của các điểm xi.
> Chú ý: Nếu f''(xi) = 0 thì ta phải dùng quy tắc 1 để xét cực trị tại xi.
* Ví dụ 1: Áp dụng quy tắc 1 (cách 1) tìm cực trị của hàm số f(x) = x(x2 - 3).
> Lời giải:
1. TXĐ: D = R
2. f’(x) = 3x2 – 3. Cho f’(x) = 0 ⇔ x = 1 hoặc x = -1.
3. Ta có bảng biến thiên:
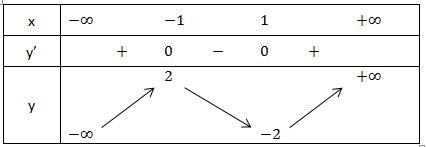
Hàm số đạt cực đại tại x = -1 và giá trị cực đại là 2
Hàm số đạt cực tiểu tại x = 1 và giá trị cực tiểu là -2.
* Ví dụ 2: Áp dụng quy tắc 2 (cách 2) tìm cực trị của hàm số:
> Lời giải:
1. TXĐ: D = R
2. Ta tính f'(x) = x3 - 4x = x(x2 - 4);
Cho f'(x) = 0 ⇔ x1 = 0; x2 = -2; x3 = 2.
- Tính f''(x) = 3x2 - 4. ta có:
f''(x1) = f''(0) = 2.02 - 4 = -4 < 0 ⇒ x1 = 0 là điểm cực đại
f''(x2) = f''(-2) = 3.(-2)2 - 4 = 8 ⇒ x2 = -2 là điểm cực tiểu
f''(x3) = f''(2) = 3.(2)2 - 4 =8 ⇒ x3 = 2 là điểm cực tiểu
- Kết luận: f(x) đạt cực đại tại x1 = 0 và fCĐ = f(0) = 6;
f(x) đạt cực tiểu tại x2 = -2, x3 = 2 và fCT = f(±2) = 2.
Từ khóa » đạt Cực Tiểu
-
Cưc đại Và Cực Tiểu Là Gì? Cách Xác định điểm Cực Trị Của Hàm Số
-
Kiến Thức Quan Trọng Về Cực đại Và Cực Tiểu Của Hàm Số
-
2. Điều Kiện để Hàm Số đạt Giá Trị Cực đại Hoặc Cực Tiểu - VOH
-
Điểm Cực đại, Cực Tiểu Của Hàm Số Là Gì ? Hai Quy Tắc Tìm Cực Trị
-
Bài 2. Cực Trị Của Hàm Số - Củng Cố Kiến Thức
-
Các Dạng Bài Tập Về Cực Trị (Cực đại, Cực Tiểu) Của Hàm Số Và Cách ...
-
Cực đại, Cực Tiểu Của đồ Thị Hàm Số, Phương Pháp Tìm Cực Trị
-
Điểm Cực đại, Cực Tiểu Của Hàm Số Là Gì ? Hai Quy ... - MarvelVietnam
-
Tìm Tham Số M để Hàm Số đạt Cực Trị Tại Một điểm Cực Hay - Toán Lớp ...
-
Hàm Số Y = (x^3) - 3x^2 + 4 đạt Cực Tiểu Tại:
-
Top 14 đạt Cực Tiểu Khi
-
Cho Hàm Số Y = F(x), Tìm Các điểm Cực đại, điểm Cực Tiểu, Giá Trị Cực ...
-
Kiến Thức Tìm M để Hàm Số đạt Cực đại Cực Tiểu - Banmaynuocnong
-
Điểm Cực Trị - Cực Đại Và Tiểu - Giá Trị Nhỏ Nhất Và Lớn Nhất