Định Lý Ta Lét Là Gì? Những Hệ Quả Của định Lý Talet
Có thể bạn quan tâm
Định lý Talet là gì? Đây là một định lý rất quan trọng của kiến thức hình học về tỷ lệ giữa các đoạn thẳng trên hai cạnh của một tam giác bị chắn bởi một đường thẳng song song mà với cạnh thứ 3. Và để tìm hiểu rõ hơn về nội dung của định lý Ta lét, những hệ quả của định lý Talets. Mời các bạn đọc của thapgiainhietliangchi.com cùng theo dõi bài viết dưới đây nhé.
Tìm hiểu tỉ số của hai đoạn thẳng là như thế nào?
Tỉ số của hai đoạn thẳng là như thế nào?
Trước khi bắt đầu tìm hiểu chi tiết về định lý Talet, chúng ta sẽ cùng nhắc qua kiến thức về tỉ số của hai đoạn thẳng đã các bạn nhé.
- Tỉ số của 2 đoạn thẳng chính là tỉ số về độ dài của chúng theo cùng một đơn vị đo nhất định. Và tỉ số của 2 đoạn thẳng sẽ không bị phụ thuộc vào cách chọn đơn vị đo.
- Tỉ số của 2 đoạn thẳng DM và HL sẽ được kí hiệu là DM/HL.
Ví dụ về tỉ số của hai đoạn thẳng: Cho trước đoạn thẳng AB và một tỉ số m/n > 0. Điểm C thuộc AB đã biết CA/CB = m/n. Khi đó, ta có thể gọi điểm C chính là điểm chia đoạn thẳng AB theo tỉ số m/n.
Đoạn thẳng tỉ lệ
Giả sử chúng ta có sẵn 2 đoạn thẳng là AB và CD. Hai đoạn thẳng này sẽ được gọi là tỉ lệ với 2 đoạn thẳng A’B’ và C’D’ nếu như có tỉ lệ thức: AB/CD = A’B’/C’D’ hoặc AB/A’B’ = CD/C’D’.
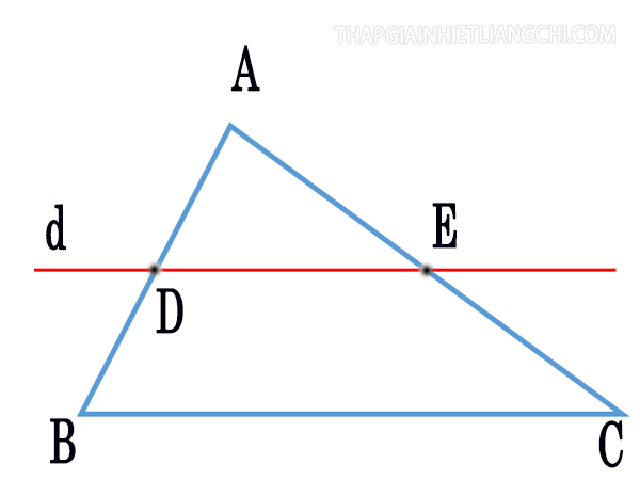
Định lý Ta-lét trong tam giác, tam giác vuông
Định lý Talet thuận trong tam giác, tam giác vuông
Định lý Talet thuận được phát biểu như sau:
Nếu như ta có một đường thẳng cắt hai cạnh của 1 tam giác và song song với cạnh còn lại thì khi đó nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
Ví dụ về định lý Talet thuận trong tam giác, tam giác vuông: Cho trước tam giác ABC, đường thẳng d cắt cạnh AB tại B’, cắt cạnh AC tại C’ và song song với cạnh BC.
Theo định lý Talet, ta có:
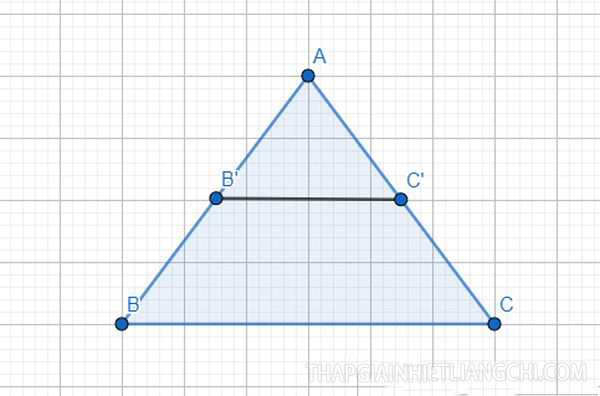

Định lý Talet đảo trong tam giác, tam giác vuông
Định lý Talet đảo trong tam giác được phát biểu như sau:
Nếu như một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó sẽ song song với cạnh còn lại của tam giác này.
Lưu ý: Định lý Talet đảo vẫn đúng cho trường hợp đường thẳng đó cắt ở phần kéo dài hai cạnh của tam giác.
Ví dụ về định lý Talet đảo trong tam giác, tam giác vuông: Với hình minh họa như ở trên, nếu trong tam giác đã cho ABC ta chứng minh được các đoạn thẳng có tỉ lệ giống như 1 trong 3 tỉ lệ sau thì theo như định lý Talet đảo ta sẽ suy ra: B’C’// BC.
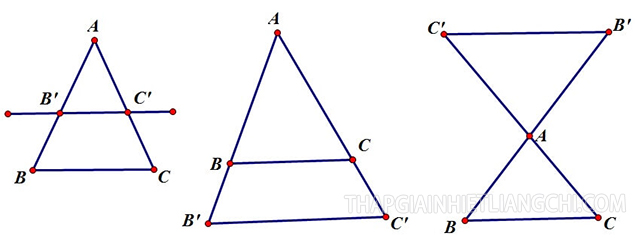
Hệ quả định lý Talet
Hệ quả của định lý Talet được phát biểu như sau:
- Hệ quả 1: Nếu như 1 đường thẳng cắt 2 cạnh của 1 tam giác và // với cạnh còn lại thì nó sẽ tạo thành một tam giác mới có 3 cạnh tương ứng tỉ lệ với 3 cạnh của tam giác trước đó.
- Hệ quả 2: Nếu như 1 đường thẳng cắt 2 cạnh của 1 tam giác và song song với cạnh còn lại thì nó sẽ tạo ra một tam giác mới đồng dạng với hình tam giác ban đầu.
- Hệ quả 3 – định lý Talet nâng cao: Nếu như 3 đường thẳng đồng quy thì khi chắn trên hai đường thẳng song song, các cặp đoạn thẳng tương ứng tỉ lệ.
Xem thêm:
- Đường trung tuyến là gì? Công thức, tính chất đường trung tuyến của tam giác
- Hình chóp là gì? Công thức tính chu vi, diện tích và thể tích hình chóp
Định lý Talet trong hình thang
Định lý Talet trong hình thang thường được phát biểu như sau:
Nếu như có 1 đường thẳng song song với 2 cạnh đáy của một hình thang và cắt 2 cạnh bên của hình thang đó thì nó sẽ định ra trên hai cạnh bên những đoạn thẳng tương ứng tỉ lệ.
Ví dụ định lý Talet trong hình thang: Cho hình thang ABCD như hình dưới:
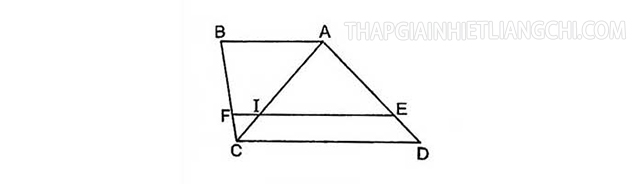
Trong hình thang ABCD, E thuộc cạnh AD, F thuộc cạnh BC.
Nếu EF song song với cạnh AB, song song với cạnh CD thì ta có: AE/DE sẽ bằng BF/CF.
Ngược lại, nếu như: AE/DE = BF/CF thì ta có thể suy ra: EF song song với cạnh AB, song song với cạnh CD.
Định lý Talet trong không gian
- Định lý thuận (Định lí Ta lét) trong không gian
Ba mặt phẳng đôi một song song, chắn trên hai đường cát tuyến bất kì, tạo ra các đoạn thẳng tương ứng tỉ lệ, nghĩa là:
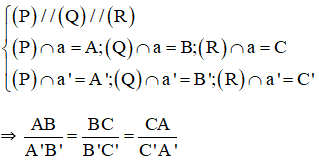
- Định lí đảo (Định lí Talet đảo) trong không gian
Giả sử như trên hai đường thẳng a và a’ lần lượt lấy hai bộ 3 điểm (A, B, C) và (A’, B’, C’) sao cho có AB/A’B’= BC/B’C’ = CA/C’A’
Khi đó suy ra ba đường thẳng AA’, BB’, CC’ sẽ cùng song song với một mặt phẳng, có nghĩa là ba đường thẳng đó sẽ nằm trên ba mặt phẳng song song với nhau.
Các dạng bài tập định lý Talet lớp 8
Dạng 1: Tính độ dài của đoạn thẳng, chu vi hay diện tích và các tỉ số
Phương pháp giải bài tập định lý Talet lớp 8:
Để giải các bài toán dạng này, ta cần sử dụng định lý Talet, hệ quả của định lý Talet cùng tỉ số đoạn thẳng để tính toán nhé.
- Định lý Talets: Nếu như 1 đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại của tam giác đó thì nó sẽ định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
- Hệ quả của định lý Talet: nếu như 1 đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại của tam giác đó thì nó sẽ tạo thành một tam giác mới có 3 cạnh tương ứng tỉ lệ với 3 của cạnh tam giác đã cho.
Ngoài ra, chúng ta còn có thể sử dụng đến tính chất của tỉ lệ thức để tính toán.
Xem thêm: Hàm số lượng giác là gì? Phương trình lượng giác cơ bản thường gặp
Dạng 2: Chứng minh 2 đường thẳng // và chứng minh các đẳng thức hình học
Để giải được các bài toán thuộc dạng này, chúng ta sẽ áp dụng linh hoạt định lý Talet thuận, định lý Talet đảo và hệ quả của định lý Talet để chứng minh nhé.
Bài viết trên đây là những kiến thức có liên quan đến định lý Ta lét cực kỳ chuẩn xác mà chúng tôi muốn chia sẻ đến các bạn. Hy vọng rằng những kiến thức này có thể giúp bạn hiểu rõ hơn về định lý Talet cũng như có thể áp dụng định lý Talet thành thạo để giải các dạng bài toán có liên quan nhé. Cảm ơn các bạn đã dành nhiều thời gian theo dõi bài viết. Chúc các bạn nghiên cứu và học tập thật tốt!
Từ khóa » định Lý Thales Và Hệ Quả
-
Lý Thuyết định Lí đảo Và Hệ Quả Của định Lí Talet | SGK Toán Lớp 8
-
Định Lý Talet Và Những Hệ Quả Của định Lý Talet
-
Định Lý Talet Thuận, định Lý Talet đảo Và Hệ Quả Của định Lý Talet
-
Định Lí đảo Và Hệ Quả Của định Lí Ta-lét
-
Định Lý Thales – Wikipedia Tiếng Việt
-
Định Lí Ta-lét. Định Lí đảo Và Hệ Quả Của định Lí Ta-lét
-
[Định Lý Talet (Thales)] Định Lý Talet Và Những Hệ Quả Của Chúng
-
Định Lý Talet Và Những Hệ Quả Của định Lý Talet - Gia Sư Thành Tài
-
Định Lý Talet Và 3 Hệ Quả Cực Kỳ Quan Trọng Cùng Bài Tập Áp Dụng
-
Tìm Hiểu Về định Nghĩa Và Những Hệ Quả Của định Lý Talet - VOH
-
Định Lý Talet [Thalet] - Định Lí đảo Và Hệ Quả Của Nó
-
Định Lý Talet Trong Tam Giác, Hệ Quả định Lý Talet Và VÍ DỤ
-
Lý Thuyết định Lí Ta-lét. định Lí đảo Và Hệ Quả Của định Lí Ta-lét Toán 8
-
Định Lý Talet Trong Tam Giác Và Những Hệ Quả Của định Lý - GiaiNgo