Định Nghĩa, ý Nghĩa, Công Thức Tính đạo Hàm - Abcdonline

Trang chủ » Tính đạo Hàm Của Delta » Định Nghĩa, ý Nghĩa, Công Thức Tính đạo Hàm - Abcdonline

Có thể bạn quan tâm

Định nghĩa, ý nghĩa, công thức tính đạo hàm

Lý thuyết Đạo hàm: Định nghĩa, ý nghĩa, quy tắc và công thức tính đạo hàm, công thức tính nhanh đạo hàm phân thức, đạo hàm cấp 2.

Bài viết này nói về kiến thức Đạo hàm lớp 11.

Đạo hàm là tỉ số giữa số gia của hàm số và số gia của đối số tại điểm x0. Giá trị của đạo hàm thể hiện chiều biến thiên của hàm số và độ lớn của biến thiên này. Đạo hàm có ý nghĩa hình học và vật lý.

1. Định nghĩa đạo hàm

Cho hàm số y=f(x)

xác định trên khoảng (a ; b) và x_{0} \in(a ; b), đạo hàm của hàm số tại điểm x_{0} là:

\displaystyle f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow x_{0}} \frac{f(x)-f\left(x_{0}\right)}{x-x_{0}}

Nếu ký hiệu: \Delta x=x-x_{0} và \Delta y=f\left(x_{0}+\Delta x\right)-f\left(x_{0}\right) thì:\displaystyle f^{\prime}\left(x_{0}\right)=\lim _{x \rightarrow \infty} \frac{f\left(x_{0}-\Delta x\right)-f\left(x_{0}\right)}{x-x_{0}}=\lim _{\Delta x \rightarrow 0} \frac{\Delta y}{\Delta x}

– Nếu hàm số có đạo hàm tại x_{0} thì nó liên tục tại điểm x_{0}.

2. Ý nghĩa của đạo hàm

• Ý nghĩa hình học của đạo hàm:

– Cho hàm số y=f(x)

có đồ thị (C).

– f^{\prime}\left(x_{0}\right) là hệ số góc tiếp tuyến của đồ thị (C) của hàm số y=f(x)

tại M_{0}\left(x_{0} ; x_{0}\right) \in(C) thì phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm M_{0} là:

y=f^{\prime}\left(x_{0}\right) \cdot\left(x-x_{0}\right)+y_{0}

• Ý nghĩa vật lý của đạo hàm:

– Vận tốc tức thời của chuyển động thẳng xác định bởi phương trình: s=s(t) tại thời điểm t_{0} là \displaystyle v({{t}_{0}})={{s}^{\prime }}({{t}_{0}}).

– Cường độ tức thời của lượng điện \displaystyle Q=Q(t) tại điểm t_{0} là \displaystyle I({{t}_{0}})={{Q}^{\prime }}({{t}_{0}}).

3. Quy tắc và công thức tính đạo hàm

– Quy tắc tính đạo hàm: Cho u=u(x) ; v=v(x) ; C: là hằng số

– Tổng, hiệu: (u \pm v)^{\prime}=u^{\prime} \pm v^{\prime}

– Tích: (u . v)^{\prime}=u^{\prime} \cdot v+v^{\prime} \cdot u \Rightarrow(C . u)^{\prime}=C . u^{\prime}

– Thương: \displaystyle\left(\frac{u}{v}\right)=\frac{u^{\prime} \cdot v-v^{\prime} \cdot u}{v^{2}},(v \neq 0) \Rightarrow\left(\frac{C}{u}\right)^{\prime}=-\frac{C \cdot u^{\prime}}{u^{2}}

– Đạo hàm hàm hợp: Nếu y=f(u), u=u(x) \Rightarrow y_{x}^{\prime}=y_{u}^{\prime} \cdot u_{x}^{\prime}.

Bảng công thức tính đạo hàm:

Tính đạo hàm của hàm sơ cấp và đạo hàm của hàm hợp như bảng tóm tắt dưới đây.

Định nghĩa, ý nghĩa, công thức tính đạo hàm

Công thức tính nhanh đạo hàm hàm phân thức:

\displaystyle\left(\frac{a x+b}{c x+d}\right)^{\prime}=\frac{a d-b c}{(c x+d)^{2}}

\displaystyle {{\left( {\frac{{a{{x}^{2}}+bx+c}}{{d{{x}^{2}}+ex+f}}} \right)}^{\prime }}=\frac{{\left| {\begin{array}{*{20}{l}} a & b \\ d & e \end{array}} \right|{{x}^{2}}+2\left| {\begin{array}{*{20}{l}} a & c \\ d & f \end{array}} \right|x+\left| {\begin{array}{*{20}{l}} b & c \\ e & f \end{array}} \right|}}{{{{{\left( {d{{x}^{2}}+ex+f} \right)}}^{2}}}}

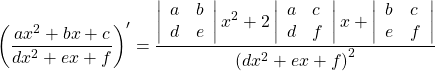
Đạo hàm cấp 2

– Định nghĩa: f^{\prime \prime}(x)=\left[f^{\prime}(x)\right]^{\prime}

– Ý nghĩa cơ học: gia tốc tức thời của chuyển động s=f(t) tại thời điểm t_{0} là: a\left(t_{0}\right)=f^{\prime \prime}\left(t_{0}\right)

Các dạng toán về đạo hàm của hàm số

– Tính đạo hàm của hàm số

– Giải phương trình đạo hàm y’ = 0

– Chứng minh đẳng thức về đạo hàm

Ví dụ tính đạo hàm có lời giải

Ví dụ 1: Tính đạo hàm của các hàm số sau

a) y=x^{3}-3 x^{2}+2 x+5

b) y=\sin x-\cos x+\tan x

c) y=x^{4}+3 \sqrt{x}

d) y=\cot x-2 x+1

Giải:

a) y=x^{3}-3 x^{2}+2 x+5

Ta có: y^{\prime}=\left(x^{3}-3 x^{2}+2 x+5\right)^{\prime}

\Rightarrow y^{\prime}=3 x^{2}-6 x+2

b) y=\sin x-\cos x+\tan x

Ta có: y^{\prime}=(\sin x-\cos x+\tan x)^{\prime}

\displaystyle\Rightarrow y^{\prime}=\cos x+\sin x+\frac{1}{\cos ^{2} x}

c) y=x^{4}+3 \sqrt{x}

Ta có: y^{\prime}=\left(x^{4}+3 \sqrt{x}\right)^{\prime}

\displaystyle\Rightarrow y^{\prime}=4 x^{3}+\frac{3}{2 \sqrt{x}}

d) y=\cot x-2 x+1

Ta có: y^{\prime}=(\cot x-2 x+1)^{\prime}

\displaystyle\Rightarrow y^{\prime}=-\frac{1}{\sin ^{2} x}-2

Bài tập đạo hàm lớp 11

Bài 1: Tính đạo hàm các hàm số sau

a) \displaystyle y=\frac{x^{2}+x+1}{x+1}

b) \displaystyle y=\frac{x^{2}-2 x+2}{x-1}

c) \displaystyle y=\frac{x^{2}-3 x}{x-1}

d) y=x^{4}-x^{2}+1

e) y=2 x^{3}+3 x^{2}-1

f) y=2 x^{3}+3 x^{2}-1

Bài 2: Tính đạo hàm các hàm số sau

a) \displaystyle y=\frac{x-2}{x-1}

b) y=x^{3}-3 x^{2}+2

c) \displaystyle y=\frac{x^{2}}{x+1}

d) \displaystyle y=\frac{-3 x+1}{x+2}

e) \displaystyle y=\frac{-3 x^{2}-x+1}{2 x-1}

f) y=-2 x^{4}+3 x^{2}-4

Bài 3: Tính đạo hàm các hàm số sau tại các điểm tương ứng

a) \displaystyle y=\frac{x^{2}+3 x+3}{x+1} tại điểm x_{0}=-1

b) y=x^{4}-5 x^{2}+4 tại điểm x_{0}=2

c) \displaystyle y=\frac{2}{3} x^{3}-5 x^{2}+2 x+4 tại điểm x_{0}=\sqrt{3}

Bài 4: Giải phương trình y^{\prime}=0 trong các trường hợp sau:

a) \displaystyle y=\frac{x^{2}+3 x+3}{x+1}

b) \displaystyle y=\frac{2 x^{2}+2}{-x+1}

c) y=x^{3}-3 x^{2}+2

d) y=x^{4}-5 x^{2}+4

e) y=-2 x^{4}-x^{2}+4

f) y=-x^{3}-3 x+2

Đại số & Giải tích 11 - Tags: công thức, công thức đạo hàm, đạo hàm, đạo hàm cấp 2, toán 11

  • Một số kỹ thuật giải phương trình lượng giác

  • Cách giải một số dạng phương trình lượng giác

  • Phương trình lượng giác cơ bản lớp 11

  • Trắc nghiệm Ứng dụng của đạo hàm – Toán lớp 11

Từ khóa » Tính đạo Hàm Của Delta