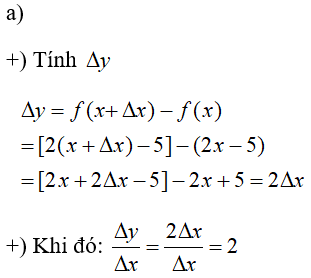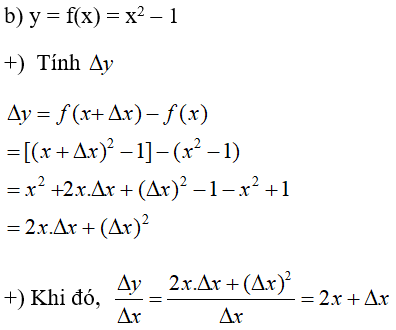Tính Delta Y Và Delta X / Delta Y Của Các Hàm Số Sau Theo X Và Delta X...

Có thể bạn quan tâm

Đăng nhập Facebook

Google

CHỌN BỘ SÁCH BẠN MUỐN XEM

Hãy chọn chính xác nhé!

Trang chủ Lớp 11 Toán

Câu hỏi:

23/07/2024 14,676

Tính Δy và ∆y∆x của các hàm số sau theo x và Δx:

a) y=2x-5;

b) y=x2-1;

c) y=2x3;

d) y=1x.

Xem lời giải Câu hỏi trong đề: Giải SGK Toán 11 Chương 5: Đạo hàm Bắt Đầu Thi Thử

Trả lời:

Giải bởi Vietjack

Gọi Δ x là số gia của biến số x.

Câu trả lời này có hữu ích không?

2 1

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết

ĐĂNG KÝ VIP

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tính (bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra:

a) y = x2+x tại x0=1

b) y=1x tại x0=2

c) y=x+1x-1 tại x0=0

Xem đáp án » 30/11/2021 7,230

Câu 2:

Bằng định nghĩa, hãy tính đạo hàm của các hàm số:

a) f(x) = x2 tại điểm x bất kì;

b) g(x) = 1/x tại điểm bất kì x ≠ 0

Xem đáp án » 30/11/2021 4,389

Câu 3:

Viết phương trình tiếp tuyến đường cong y=x3.

a. Tại điểm (-1; -1);

b. Tại điểm có hoành độ bằng 2;

c. Biết hệ số góc của tiếp tuyến bằng 3.

Xem đáp án » 30/11/2021 4,261

Câu 4:

Bài 7 (trang 157 SGK Đại số 11): Một vật rơi tự do theo phương trình s = 1/2 gt2, trong đó g≈9,8m/s2 là gia tốc trọng trường.

a. Tìm vận tốc trung bình của chuyển động trong khoảng thời gian từ t (t = 5s) đến t + Δt, trong các trường hợp Δt=0,1s; Δt=0,05s; Δt=0,001s.

b. Tìm vận tốc tức thời của chuyển động tại thời điểm t = 5s.

Xem đáp án » 30/11/2021 2,924

Câu 5:

Viết phương trình tiếp tuyến của hypebol: y=1x

a) Tại điểm 12;2 ;

b) Tại điểm có hoành độ bằng -1;

c) Biết rằng hệ số góc của tiếp tuyến bằng -14.

Xem đáp án » 30/11/2021 2,610

Câu 6:

a) Vẽ đồ thị của hàm số f(x) = x22

b) Tính f’(1).

c) Vẽ đường thẳng đi qua điểm M(1; 1/2) và có hệ số góc bằng f’(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.

Xem đáp án » 30/11/2021 1,730

Câu 7:

Cho hàm số y = x2. Hãy tính y'(xo) bằng định nghĩa.

Xem đáp án » 30/11/2021 1,226

Câu 8:

Tìm số gia của hàm số f(x) = x3, biết rằng:

a.x0 = 1; Δx = 1;

b.x0 = 1; Δx = -0,1;

Xem đáp án » 30/11/2021 728

Câu 9:

Viết phương trình đường thẳng đi qua Mo(xo; yo) và có hệ số góc λ

Xem đáp án » 30/11/2021 504

Câu 10:

Một đoàn tàu chuyển động khởi hành từ một nhà ga. Quãng đường s (mét) đi được của đoàn tàu là một hàm số của thời gian t (phút). Ở những phút đầu tiên, hàm số đó là s = t2.

Hãy tính vận tốc trung bình của chuyển động trong khoảng [t; to] với to = 3 và t = 2; t = 2,5; t = 2,9; t = 2,99.

Nêu nhận xét về những kết quả thu được khi t càng gần to = 3.

Xem đáp án » 30/11/2021 493

Câu 11:

Chứng minh rằng hàm số:

f(x)=x-12 (nếu x≥0)-x2 (nếu x<0)

Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2.

Xem đáp án » 30/11/2021 372 Xem thêm các câu hỏi khác »

Đề thi liên quan

Xem thêm »

Trắc nghiệm tổng hơp Toán 11 (có đáp án) 76 đề 23614 lượt thi Thi thử
Trắc nghiệm Đề thi Toán 11 (có đáp án) 17 đề 8430 lượt thi Thi thử
Trắc nghiệm Toán 11 Ôn tập chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án) 12 đề 4991 lượt thi Thi thử
Trắc nghiệm Toán 11 Ôn tập chương 4: Giới hạn (có đáp án) 7 đề 4238 lượt thi Thi thử
Trắc nghiệm Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (có đáp án) 8 đề 3941 lượt thi Thi thử
Trắc nghiệm Toán 11 Ôn tập chương 5: Đạo hàm (có đáp án) 11 đề 3842 lượt thi Thi thử
Trắc nghiệm Toán 11 Ôn tập chương 2: Tổ hợp - Xác suất (có đáp án) 15 đề 3314 lượt thi Thi thử
Trắc nghiệm Toán 11 Bài 1: Hàm số lượng giác (có đáp án) 6 đề 3234 lượt thi Thi thử
Trắc nghiệm Toán 11 Bài 2: Phương trình lượng giác cơ bản (có đáp án) 6 đề 3145 lượt thi Thi thử
Trắc nghiệm Biến cố và xác suất của biến cố có đáp án 4 đề 3085 lượt thi Thi thử

Xem thêm » Hỏi bài

Câu hỏi mới nhất

Xem thêm »

Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

\(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

Khi quay một vòng lần thứ nhất tính từ thời điểm t = 0 (phút), tại thời điểm nào của t thì cabin ở vị trí cao nhất? Ở vị trí đạt được chiều cao là 86 m?
261 18/04/2024 Xem đáp án
Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

\(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

Khi t = 0 (phút) thì khoảng cách từ cabin đến mặt đất bằng bao nhiêu?
143 18/04/2024 Xem đáp án
Một vòng quay trò chơi có bán kính 57 m, trục quay cách mặt đất 57,5 m, quay đều mỗi vòng hết 15 phút. Khi vòng quay quay đều, khoảng cách h (m) từ một cabin gắn tại điểm A của vòng quay đến mặt đất được tính bởi công thức:

\(h\left( t \right) = 57\sin \left( {\frac{{2\pi }}{{15}}t - \frac{\pi }{2}} \right) + 57,5\)

với t là thời gian quay của vòng quay tính bằng phút (t ≥ 0) (Hình 12).

Tính chu kì của hàm số h(t)?
125 18/04/2024 Xem đáp án
Từ đồ thị hàm số y = sin x, tìm:
Các khoảng giá trị của x để hàm số y = sin x nhận giá trị dương. 131 18/04/2024 Xem đáp án
Từ đồ thị hàm số y = sin x, tìm:

Các giá trị của x để sin x = \(\frac{1}{2}\);
123 18/04/2024 Xem đáp án
Từ đồ thị hàm số y = cos x, cho biết:

Có bao nhiêu giá trị của x trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{3\pi }}{2}} \right)\) để cos x = 0.
119 18/04/2024 Xem đáp án
Từ đồ thị hàm số y = cos x, cho biết:

Có bao nhiêu giá trị của x trên đoạn [ – 5π; 0] để cos x = 1;
120 18/04/2024 Xem đáp án
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

y = cosx trên khoảng (19π; 20π), (– 30π; – 29π).
123 18/04/2024 Xem đáp án
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:

y = sin x trên khoảng \(\left( { - \frac{{19\pi }}{2};\, - \frac{{17\pi }}{2}} \right),\,\,\left( { - \frac{{13\pi }}{2};\, - \frac{{11\pi }}{2}} \right)\);
124 18/04/2024 Xem đáp án
Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số:

\(y = \frac{1}{{4 - \sin x}}\).
130 18/04/2024 Xem đáp án

Xem thêm »

Từ khóa » Tính đạo Hàm Của Delta

CHỌN BỘ SÁCH BẠN MUỐN XEM

Câu hỏi:

Trả lời:

Gọi Δ x là số gia của biến số x.

Câu trả lời này có hữu ích không?

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Tính (bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra: a) y = x2+x tại x0=1 b) y=1x tại x0=2 c) y=x+1x-1 tại x0=0

Câu 2:

Bằng định nghĩa, hãy tính đạo hàm của các hàm số: a) f(x) = x2 tại điểm x bất kì; b) g(x) = 1/x tại điểm bất kì x ≠ 0

Câu 3:

Viết phương trình tiếp tuyến đường cong y=x3. a. Tại điểm (-1; -1); b. Tại điểm có hoành độ bằng 2; c. Biết hệ số góc của tiếp tuyến bằng 3.

Câu 4:

Câu 5:

Viết phương trình tiếp tuyến của hypebol: y=1x a) Tại điểm 12;2 ; b) Tại điểm có hoành độ bằng -1; c) Biết rằng hệ số góc của tiếp tuyến bằng -14.

Câu 6:

a) Vẽ đồ thị của hàm số f(x) = x22 b) Tính f’(1). c) Vẽ đường thẳng đi qua điểm M(1; 1/2) và có hệ số góc bằng f’(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.

Câu 7:

Cho hàm số y = x2. Hãy tính y'(xo) bằng định nghĩa.

Câu 8:

Tìm số gia của hàm số f(x) = x3, biết rằng: a.x0 = 1; Δx = 1; b.x0 = 1; Δx = -0,1;

Câu 9:

Viết phương trình đường thẳng đi qua Mo(xo; yo) và có hệ số góc λ

Câu 10:

Câu 11:

Chứng minh rằng hàm số: f(x)=x-12 (nếu x≥0)-x2 (nếu x<0) Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2.

Đề thi liên quan

Câu hỏi mới nhất

Liên Hệ

Tính (bằng định nghĩa) đạo hàm của mỗi hàm số tại các điểm đã chỉ ra:

a) y = x2+x tại x0=1

b) y=1x tại x0=2

c) y=x+1x-1 tại x0=0

Bằng định nghĩa, hãy tính đạo hàm của các hàm số:

a) f(x) = x2 tại điểm x bất kì;

b) g(x) = 1/x tại điểm bất kì x ≠ 0

Viết phương trình tiếp tuyến đường cong y=x3.

a. Tại điểm (-1; -1);

b. Tại điểm có hoành độ bằng 2;

c. Biết hệ số góc của tiếp tuyến bằng 3.

Viết phương trình tiếp tuyến của hypebol: y=1x

a) Tại điểm 12;2 ;

b) Tại điểm có hoành độ bằng -1;

c) Biết rằng hệ số góc của tiếp tuyến bằng -14.

a) Vẽ đồ thị của hàm số f(x) = x22

b) Tính f’(1).

c) Vẽ đường thẳng đi qua điểm M(1; 1/2) và có hệ số góc bằng f’(1). Nêu nhận xét về vị trí tương đối của đường thẳng này và đồ thị hàm số đã cho.

Tìm số gia của hàm số f(x) = x3, biết rằng:

a.x0 = 1; Δx = 1;

b.x0 = 1; Δx = -0,1;

Chứng minh rằng hàm số:

f(x)=x-12 (nếu x≥0)-x2 (nếu x<0)

Không có đạo hàm tại điểm x = 0 nhưng có đạo hàm tại điểm x = 2.