Giải Bài 1, 2, 3 Trang 40 Sách Giáo Khoa Hình Học 10

Trang chủ » Giải Toán Hình 10 Bài 1 Chương 2 Trang 40 » Giải Bài 1, 2, 3 Trang 40 Sách Giáo Khoa Hình Học 10

Có thể bạn quan tâm

Bài 1 sgk trang 40 hình học 10

 Chứng minh rằng trong tam giác \(ABC\) ta có:

a) \(\sin A = \sin (B + C)\);                          

b) \(\cos A = -\cos (B + C)\)

Giải

Trong một tam giác thì tổng các góc là \(180^0\)  :

\(\widehat{A}\) + \(\widehat{B}\) + \(\widehat{C} = 180^0\)                 

\(\Rightarrow\widehat{A}  = 180^0\) - (\(\widehat{B}\) + \(\widehat{C}\) )

\(\widehat{A}\) và  (\(\widehat{B}\) +\(\widehat{C}\) ) là \(2\) góc bù nhau, do đó:

a) \(\sin A = \sin[180^0 - (\widehat{B} +\widehat{C} )] = \sin (B + C)\)

b) \(\cos A = \cos[180^0- (\widehat{B} +\widehat{C} )] = -\cos (B + C)\)

 

Bài 2 sgk trang 40 hình học 10

Cho \(AOB\) là tam giác cân tại \(O\) có \(OA = a\) và có các đường cao \(OH\) và \(AK\). Giả sử \(\widehat {AOH} = \alpha \). Tính \(AK\) và \(OK\) theo \(a\) và \(α\).

Giải

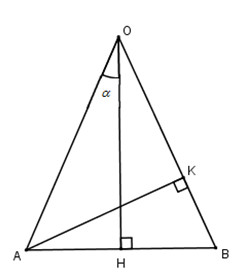
Do tam giác \(OAB\) cân tại \(O\) nên ta có \(\widehat {AOB} = 2\alpha \) 

Tam giác \(OKA\)  vuông tại \(K\) nên ta có:

\(AK = OA.\sin \widehat {AOK} \Rightarrow AK = a.\sin 2\alpha \)

\(OK = OA.cos\widehat {AOK} \Rightarrow OK = a.cos2\alpha \)

 

Bài 3 sgk trang 40 hình học 10

Chứng minh rằng :

a)  \(\sin {105^0} = \sin {75^0}\);          

b)  \(\cos {170^0} =  - \cos {10^0}\)                   

c)  \(\cos {122^0} =  - \cos {58^0}\)

Giải

a) \(\sin {105^0} = \sin ({180^0} - {105^0})\)

\(\Rightarrow \sin {105^0} = \sin {75^0}\)

b) \(\cos {170^0} =  - \cos ({180^0} - {170^0}) \)

\(\Rightarrow \cos {170^0} =  - \cos {10^0}\)

c) \(\eqalign{ & \cos {122^0} = - \cos ({180^0} - {122^0}) \cr & \Rightarrow \cos {122^0} = - \cos {58^0} \cr} \)

 

Giaibaitap.me

Từ khóa » Giải Toán Hình 10 Bài 1 Chương 2 Trang 40