Giới Hạn Hàm Số Lượng Giác Và Bài Tập ứng Dụng - TÀI LIỆU RẺ
Có thể bạn quan tâm
Tóm tắt tài liệu
- 1. Tìm giới hạn của hàm số khi \[x\to 0\] và sử dụng định lí \[\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin x}{x}=1\]
- Áp dụng vào bài toán tính giới hạn hàm số lượng giác sau khi đã biến đổi công thức về dạng chuẩn của định lí 1:
- 2. Tìm giới hạn của hàm số lượng giác khi \[x\to a\]. Dùng phép biến đổi lượng giác hoặc đổi biến số \[t=x-a\] để đưa về việc tìm giới hạn hàm số khi \[t\to 0\]
- 3. Bài tập đề nghị tính giới hạn hàm số lượng giác
- Xem thêm video
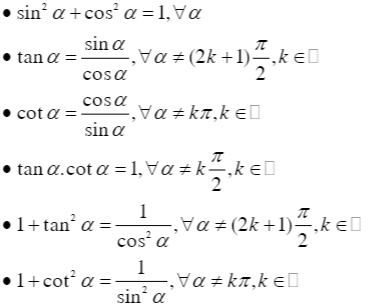
1. Tìm giới hạn của hàm số khi \[x\to 0\] và sử dụng định lí \[\underset{x\to 0}{\mathop{\lim }}\,\frac{\sin x}{x}=1\]
Để tính giới hạn hàm số lượng giác theo định lí 1, chúng ta cần phải nắm vững một số công thức lượng giác sau đây:
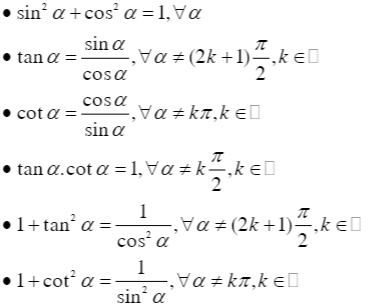
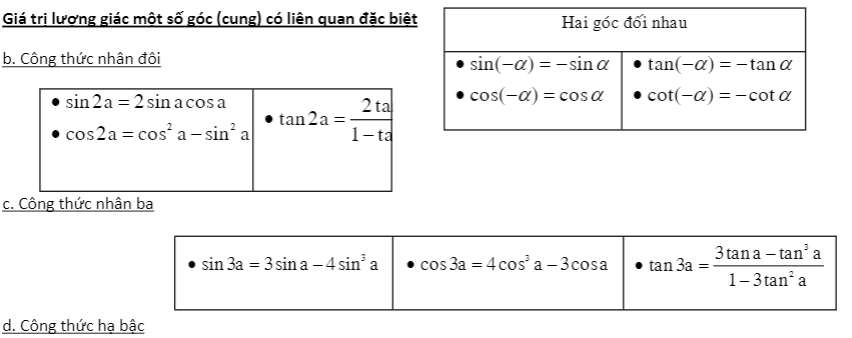

Áp dụng vào bài toán tính giới hạn hàm số lượng giác sau khi đã biến đổi công thức về dạng chuẩn của định lí 1:
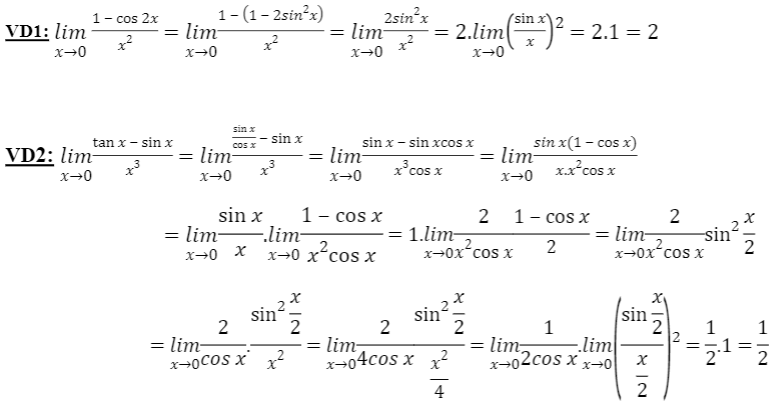
2. Tìm giới hạn của hàm số lượng giác khi \[x\to a\]. Dùng phép biến đổi lượng giác hoặc đổi biến số \[t=x-a\] để đưa về việc tìm giới hạn hàm số khi \[t\to 0\]
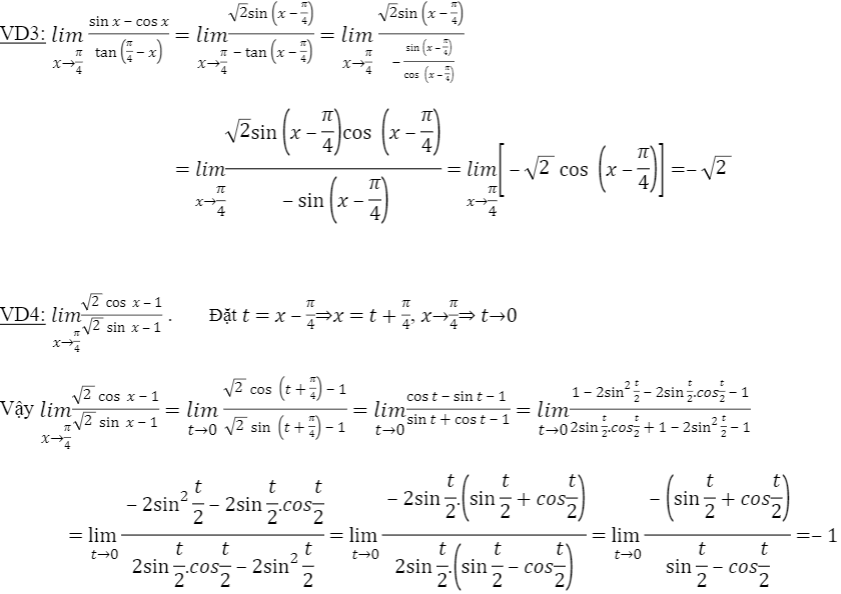
3. Bài tập đề nghị tính giới hạn hàm số lượng giác

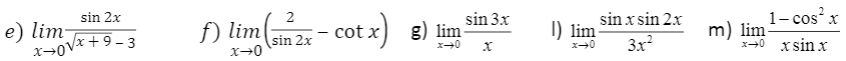
Để tải tài liệu trên, các em có thể truy cập tại đây:
CLICK VÀO ĐÂY ĐỂ TẢI TÀI LIỆUXem thêm video
Từ khóa: giới hạn hàm số lượng giác, lượng giác, giới hạn, bài tập, trắc nghiệm.
Chuyên mục: Giới hạn hàm số
Từ khóa » Giới Hạn Hàm Số Lượng Giác Nâng Cao
-
Giới Hạn Hàm Số Lượng Giác - Chuyên đề Giải Tích 11
-
Cách Tính Giới Hạn Của Hàm Số Lượng Giác Cực Hay, Chi Tiết
-
Tính Giới Hạn Của Hàm Số Lượng Giác
-
Bài Giảng Toán 11 - 4.7 GIỚI HẠN HÀM SỐ LƯỢNG GIÁml
-
Giới Hạn Dạng 0/0 Và Giới Hạn Hàm Số Lượng Giác – Môn Toán Lớp 11
-
Toán 11 - Giới Hạn Hàm Số Lượng Giác Nâng Cao - HOCMAI Forum
-
Cách Tính Giới Hạn Của Hàm Số Lượng Giác Cực Hay, Chi Tiết - Haylamdo
-
Tài Liệu Bồi Dưỡng Tự Chọn Nâng Cao Giới Hạn Của Dãy Số Và Hàm Số
-
Chuyên đề Giới Hạn Có đáp án Và Lời Giải Chi Tiết - Đặng Việt Đông
-
Các Dạng Bài Tập Giới Hạn Hàm Số Lớp 11 Từ Căn Bản Tới Nâng Cao
-
Cách Tính Giới Hạn Của Hàm Số Lượng Giác Cực ...
-
Tổng Quan Về Hàm Số Lượng Giác Và Phương Trình Hàm Số Lượng Giác
-
[PDF] BÀI 1: HÀM SỐ, GIỚI HẠN VÀ LIÊN TỤC - Topica
-
Bài 1. Các Hàm Số Lượng Giác - Ong Học Hỏi