Góc Có đỉnh Bên Trong đường Tròn, Góc Có đỉnh Bên Ngoài đường Tròn

1. Trang chủ
2. Lý thuyết toán học
3. Toán 9
4. CHƯƠNG 7: GÓC VỚI ĐƯỜNG TRÒN
5. Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn

Góc có đỉnh bên trong đường tròn, góc có đỉnh bên ngoài đường tròn Trang trước Mục Lục Trang sau

1. Các kiến thức cần nhớ

a. Góc có đỉnh bên trong đường tròn

Định nghĩa: Trong hình $1$ , góc $BIC$ nằm trong đường tròn $(O)$ được gọi là góc có đỉnh ở bên trong đường tròn.

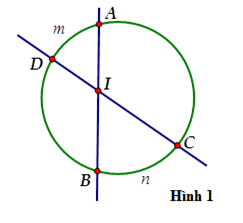
Định lý: Số đo của góc đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Ví dụ: Trong hình \(1\), $\widehat {BIC} = \dfrac{1}{2}$ $(sđ \overparen{BC} + sđ \overparen{AD})$.

b. Góc có đỉnh bên ngoài đường tròn

Định nghĩa: Góc có đỉnh nằm bên ngoài đường tròn và các cạnh đều có điểm chung với đường tròn (hình \(2,3,4\) ) là góc có đỉnh bên ngoài đường tròn.

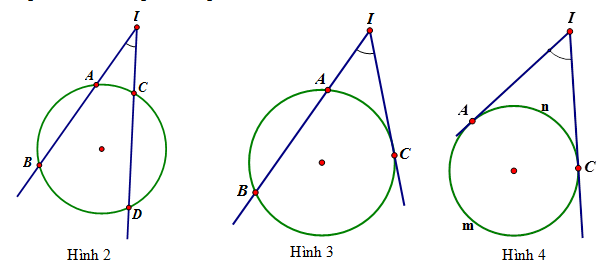
Định lý: Số đo của góc có đỉnh bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Ví dụ: Trong hình \(2\) , \(\widehat {BID} = \dfrac{1}{2}\) $(sđ \overparen{BD} - sđ \overparen{AC})$

Trong hình \(3\) , \(\widehat {BIC} = \dfrac{1}{2}\) $(sđ \overparen{BC} - sđ \overparen{AC})$

Trong hình \(4\) , \(\widehat {AIC} = \dfrac{1}{2}\) $(sđ \overparen{AmC} - sđ \overparen{AnC})$

2. Các dạng toán thường gặp

Dạng 1: Chứng minh hai góc hoặc hai đoạn thẳng bằng nhau. Tính góc và độ dài đoạn thẳng

Phương pháp:

+ Ta thường sử dụng các kiến thức về số đo của góc có đỉnh bên trong và bên ngoài đường tròn, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau

+ Sử dụng định lý Pytago, hệ thức lượng trong tam giác vuông để tính toán.

Dạng 2: Chứng minh hai đường thẳng song song, hai đường thẳng vuông góc, chứng minh các hệ thức.

Phương pháp:

+ Ta thường sử dụng các kiến thức về số đo của góc có đỉnh bên trong và bên ngoài đường tròn, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau

+) Sử dụng quan hệ từ vuông góc đến song song.

Trang trước Mục Lục Trang sau

Có thể bạn quan tâm:

• Ôn tập chương 7: Góc với đường tròn
• Góc nội tiếp
• Góc ở tâm-Số đo cung
• Ôn tập chương 5: Góc
• Ôn tập chương VI

Tài liệu

Toán 7 - Phiếu bài tập - Hai đường thẳng vuông góc (Lý thuyết + Bài tập)

Các định lí về hình học phẳng tập I - Bồi dưỡng học sinh giỏi toán cấp 2

Toán 11: Bài tập trắc nghiệm hai mặt phẳng vuông góc có đáp án và lời giải

Toán 11: Bài tập trắc nghiệm hai đường thẳng vuông góc có đáp án và lời giải

Toán 12 - Thể tích cơ bản - Cạnh bên vuông góc với đáy