Hàm Số Lũy Thừa Là Gì? Cách Tính đạo Hàm Của Hàm Số ... - KhoiA.Vn
Có thể bạn quan tâm
Cụ thể, hàm số lũy thừa là gì? cách tính đạo hàm của hàm số lũy thừa ra sao? Khảo sát hàm số lũy thừa như thế nào? chúng ta cùng tìm hiểu qua bài viết dưới đây nhé.
I. Khái niệm hàm số lũy thừa
• Hàm số lũy thừa là gì?
- Hàm số lũy thừa là các hàm số có dạng y = xα (với α ∈ R).
> Lưu ý:
- Các hàm số lũy thừa có tập xác định khác nhau, tùy theo α.
- Nếu α nguyên dương, tập xác định là R;
- Nếu α nguyên âm hoặc bằng 0, tập xác định là R\{0};
- Nếu α không nguyên, tập xác định là (0;+∞)
* Ví dụ: Hàm số: có tập xác định là [0;+∞)
Hàm số có tập xác định (0;+∞)
Hàm số có tập xác định R
Hàm số có tập xác định (0;+∞)
Như vậy, và
(hay
và
) là những hàm số khác nhau.
II. Đạo hàm của hàm số lũy thừa với số mũ tổng quát
• Hàm số y = xα có đạo hàm tại mọi x ∈ (0;+∞) và:
y' = (xα)'= α.xα-1
* Ví dụ: Tính đạo hàm của hàm: y = x3
> Lời giải:
- Áp dụng công thức (với α = 3) ta được: y' = (x3)' = 3x2.
• Nếu hàm số u = u(x) nhận giá trị dương và có đạo hàm trong khoảng J thì hàm số y = uα(x) cũng có đạo hàm trên J và:
y' = [u(xα)]'= α.uα-1(x).u'(x)
* Ví dụ: Tính đạo hàm của hàm: y = (x2 + 3x - 4)3
> Lời giải:
- Áp dụng công thức hàm hợp (với α = 3; u = x2 + 3x - 4), ta được:
y' = [(x2 + 3x - 4)3]' = 3.(x2 + 3x - 4)2.(2x + 3).
III. Khảo sát hàm số lũy thừa y = xα
Tương tự bài toán khảo sát hàm số đã học ở chương 1, khảo sát hàm số lũy thừa y=xα cũng tuân thủ đầy đủ các bước thực hiện sau:
- Bước 1: Tìm tập xác định (hay còn gọi là tập khảo sát).
- Bước 2: Xét sự biến thiên (biểu diễn bằng bảng biến thiên hàm số).
- Bước 3: Vẽ đồ thị hàm số đã cho (dựa vào bảng biến thiên bước 2).
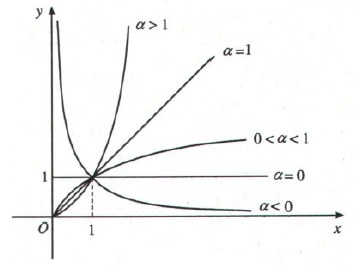 - Hình trên là đồ thị hàm số lũy thừa trên khoảng (0;+∞) ứng với các giá trị α khác nhau
- Hình trên là đồ thị hàm số lũy thừa trên khoảng (0;+∞) ứng với các giá trị α khác nhau
- Đồ thị của hàm số y = xα luôn đi qua điểm (1;1);
- Khi khảo sát hàm lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó.
Từ khóa » đạo Hàm Hàm Số Lũy Thừa Có Căn
-
Bài 2: Hàm Số Lũy Thừa - Tìm đáp án, Giải Bài Tập, để Học Tốt
-
Cách Tính đạo Hàm Của Hàm Số Lũy Thừa
-
Tính đạo Hàm Của Hàm Số Lũy Thừa, Hàm Số Mũ Và Hàm Số Logarit
-
Cách Tính đạo Hàm Của Hàm Số Lũy Thừa Nhanh, Chính Xác
-
Bảng đạo Hàm Của Các Hàm Số Cơ Bản (thường Gặp) - MathVn.Com
-
Hàm Số Lũy Thừa Và Hàm Số Mũ, Trắc Nghiệm Toán Học Lớp 12
-
Công Thức Đạo Hàm Log, Căn Bậc 3 , Căn U, Căn X, Căn Logarit
-
Đầy đủ Lý Thuyết Và Bài Tập đạo Hàm Mũ Và Logarit
-
- Đạo Hàm Cấp Cao Hàm Lũy Thừa Có Chứa Căn Thức - YouTube
-
Tập Xác định Của Hàm Số Mũ, Lũy Thừa, Logarit Cực đơn Giản [VD ...
-
Công Thức đạo Hàm: Log, Logarit, Căn Bậc 3, Căn X, Lượng Giác Chuẩn ...
-
Hàm Số Lũy Thừa Là Gì? Đao Hàm Hàm Số Lũy Thừa Toán 12
-
Lý Thuyết Hàm Số Lũy Thừa, Số Mũ - ôn Luyện Toán Cấp 3