Hệ Phương Trình đối Xứng Loại 1, Cách Giải Và Bài Tập Vận Dụng
Có thể bạn quan tâm
Vậy hệ phương trình đối xứng loại 1 có dạng như thế nào? cách giải hệ phương trình đối xứng loại 1 ra sao? chúng ta sẽ làm biết trong bài viết này và qua đó vận dụng giải minh họa một số bài tập về hệ phương trình đối xứng loại 1.
» Đừng bỏ lỡ: Cách giải Bài tập hệ phương trình đối xứng loại 2 cực hay
• Hệ phương trình đối xứng loại 1
- Hệ phương trình đối xứng loại 1 có dạng: 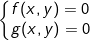 trong đó
trong đó 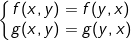
* Ví dụ: Hệ phương trình đối xứng loại 1: 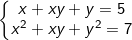
• Định lý Vi-ét cho phương trình bậc 2
- Nếu phương trình bậc hai ax2 + bx + c = 0 có 2 nghiệm phân biệt x1, x2 thì
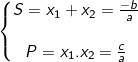
- Ngược lại, nếu hai số x1, x2 có: 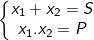 thì x1, x2 là nghiệm của phương trình:
thì x1, x2 là nghiệm của phương trình:
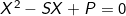

• Cách giải hệ phương trình đối xứng loại 1
+ Bước 1: Biểu diễn từng phương trình của hệ qua x+y và xy.
+ Bước 2: Đặt S = x + y, P = xy. Điều kiện hệ có nghiệm là S2 ≥ 4P. Ta được hệ mới chứa ẩn S và P.
+ Bước 3: Giải hệ phương trình với ẩn S, P để tìm ra S và P (sử dụng phương pháp thế hoặc cộng đại số).
+ Bước 4: Tìm được S và P, khi đó x và y là nghiệm của phương trình bậc hai:
X2 - SX + P = 0
+ Bước 5: Kết luận nghiệm của hệ phương trình.
* Lưu ý: Vì hệ phương trình là đối xứng nên nếu (x0;y0) là nghiệm của hệ thì (y0;x0) cũng là nghiệm của hệ phương trình.
• Bài tập về hệ phương trình đối xứng loại 1 có lời giải
* Bài tập 1: Giải hệ phương trình đối xứng loại 1 sau: 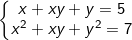 (I)
(I)
* Lời giải:
- Ta có: 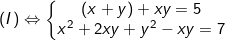
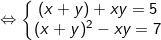
Đặt S = x + y; P = xy điều kiện S2 ≥ 4P, ta được:
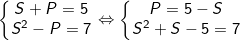
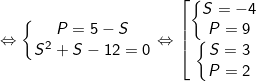
Mà S2 ≥ 4P nên ta thấy chỉ có S = 3, P = 2 thỏa mãn.
Khi đó: x, y là nghiệm của phương trình bậc hai: X2 - 3X + 2 = 0
⇔ (X - 1)(X - 2) = 0 ⇔ X = 1 hoặc X = 2.
Vậy hệ phương trình có nghiệm là (1;2), (2;1).
* Bài tập 2: Giải hệ phương trình đối xứng loại 1 sau: 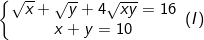
* Lời giải:
- Điều kiện: x≥0, y≥0;
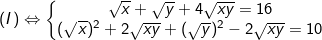
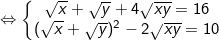
Đặt 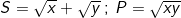
Điều kiện S≥0; P≥0 và S2 ≥ 4P. khi đó hệ (I) trở thành:
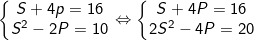
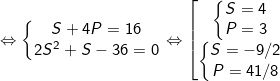
Ta thấy S, P ≥0 và S2 ≥ 4P nên chỉ có S = 4; P = 3 thỏa điều kiện.
Khi đó √x và √y là 2 nghiệm của phương trình: X2 - 4X + 3 = 0
⇔ (X - 1)(X - 3) = 0 ⇔ X = 1 hoặc X = 3.
- Trường hợp 1: 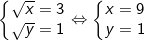
- Trường hợp 2: 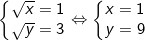
Ta thấy cả 2 cặp nghiệp đều thỏa mãn.
Vậy hệ phương trình có hai nghiệm: (x;y) = {(1;9); (9;1)}.
* Bài tập 3: Cho hệ phương trình đối xứng loại 1 có tham số m: 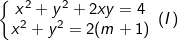
Tìm m để hệ phương trình đối xứng trên có đúng hai nghiệm.
* Lời giải:
- Ta có: 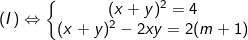
Đặt S = x + y; P = xy khi đó (I) trở thành:
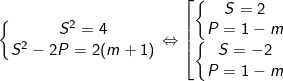
Khi đó (x;y) là nghiệm của phương trình bậc hai:
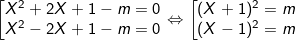
Như vậy để hệ có nghiệm duy nhât thì m = 0; khi đó 2 ngiệm của hệ là: (x;y) = {(1;1); (-1;-1)}.
* Bài tập 4: Giải hệ phương trình đối xứng loại 1: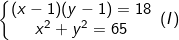
* Lời giải:
- Ta có: 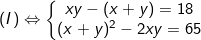
Đặt S = x + y; P = xy với điều kiện S2 ≥ 4P. Ta có hệ
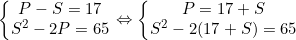
Từ: S2 - 2(17 + S) = 65
⇔ S2 - 2S - 99 = 0
⇔ (S + 9)(S - 11) = 0
⇔ S = -9 hoặc S = 11
+ Với S = -9 ⇒ P = 8 (thỏa), Khi đó x và y là nghiệm của phương trình bậc hai.
X2 + 9X + 8 = 0 ⇔ (X + 1)(X + 8) = 0 ⇔ X = -1 hoặc X = -8
⇒ hệ có 2 nghiệm là: (x;y) = {(-1;-8); (-8;-1)};
+ Với S = 11 ⇒ P = 28 (thỏa), Khi đó x và y là nghiệm của phương trình bậc hai.
X2 - 11X + 28 = 0 ⇔ (X - 4)(X - 7) = 0 ⇔ X = 4 hoặc X = 7
⇒ hệ có 2 nghiệm là: (x;y) = {(4;7); (7;4)};
- Kết luận: Vậy hệ phương trình có 4 nghiệm là: (x;y) = {(-1;-8); (-8;-1); (4;7); (7;4)}.
* Bài tập 5: Giải hệ phương trình đối xứng loại 1 sau: 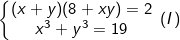
* Lời giải:
- Ta có: 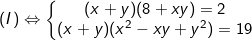
![\small \Leftrightarrow \left\{\begin{matrix} (x+y)(8+xy)=2\\ (x+y)[(x+y)^2-3xy]=19 \end{matrix}\right.](https://hayhochoi.vn/uploads/news/wyswyg/2021_07/1626344043up31vzfke8_1626422434.gif)
Đặt S = x + y; P = xy với điều kiện S2 ≥ 4P. Ta có hệ
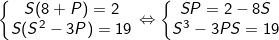
Ta thế: SP = 2 - 8S vào S3 - 3PS = 19 được:
S3 - 3(2 - 8S) = 19
⇔ S3 + 24S - 25 = 0 (nhẩm thấy có nghiệm S = 1) nên
⇔ (S - 1)(S2 + S + 25) = 0 ⇔ S = 1
(vì S2 + S + 25 = (S + 1/2)2 + 99/4 ≥ 99/4 với mọi S).
+ Với S = 1 ⇒ P = – 6 (thỏa), khi đó x và y là nghiệm của phương trình bậc hai.
X2 - X - 6 = 0 ⇔ (X + 2)(X - 3) = 0 ⇔ X = -2 hoặc X = 3.
Vậy hệ có 2 nghiệm là: (x;y) = {(3;-2); (-2;3)}.
Từ khóa » Các Giải Hệ Phương Trình đối Xứng Loại 1
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1
-
Hệ Phương Trình đối Xứng Loại 1
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1 Cực Hay - Toán Lớp 9
-
Hệ Phương Trình đối Xứng Loại 1
-
Hệ Phương Trình đối Xứng Loại 1 - Mẹo Giải Nhanh Và Bài Tập Vận Dụng
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1, Loại 2 - Học Toán 123
-
Chuyên đề: Hệ Phương Trình đối Xứng - Trường Quốc Học
-
Hệ Phương Trình đối Xứng Là Gì? Định Nghĩa, Cách Nhận Biết Và Bài Tập
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1 Cực Hay | Toán Lớp 9
-
Bài Tập Về Hệ Phương Trình đối Xứng Loại 1 - 123doc
-
Hệ Phương Trình đối Xứng Loại 1 Chứa Căn - 123doc
-
Cách Giải Hệ Phương Trình đối Xứng Loại 1 Cực Hay
-
Hệ Phương Trình - đỗi Xứng Loại 1 - YouTube
-
Hệ Phương Trình đối Xứng Loại 1 | Mathoflife