Hình Học 10/Chương I/§3. Tích Của Vectơ Với Một Số - VLOS
Có thể bạn quan tâm



Mục lục
- 1 Lí thuyết
- 1.1 Định nghĩa
- 1.2 Tính chất
- 1.3 Trung điểm của đoạn thẳng và trọng tâm của tam giác
- 1.4 Điều kiện để hai vectơ cùng phương
- 1.5 Phân tích một vectơ theo hai vectơ không cùng phương
- 2 BÀI TẬP
Lí thuyết[sửa]
| Hoạt động 1 | 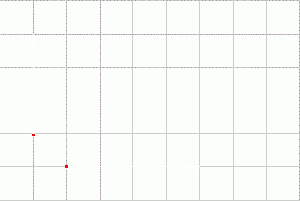 Cho hai vectơ 1) Vẽ vectơ 2) Vẽ vectơ Nhận xét gì về hướng và độ dài của vectơ |
Định nghĩa[sửa]
Cho số k ≠ 0 và vectơ 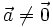 . Tích của vectơ . Tích của vectơ  với số k là một vectơ: với số k là một vectơ:
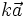 . . |
Ta quy ước 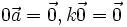 .
.
Người ta còn gọi tích của vectơ với một số là tích của một số với một vectơ.
| Hoạt động 2 | 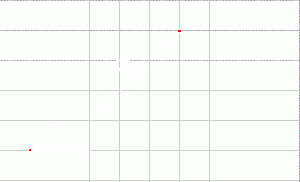  và vectơ và vectơ  (hình 13p2). (hình 13p2). 1) Vẽ vectơ 2) Tích của vectơ |
| VÍ DỤ 1 | 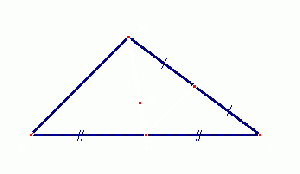 Cho G là trọng tâm của tam giác ABC, D và E lần lượt là trung điểm của BC và AC (h.1-13). Ta có: |
NHẬN XÉT:
- Với một vectơ a và số k cho trước, ta có thể vẽ được vô số vectơ
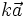 .
. -
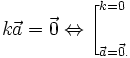
- Vectơ
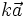 và vectơ
và vectơ  luôn cùng phương với nhau.
luôn cùng phương với nhau.
Tính chất[sửa]
Với hai vectơ  và và  bất kì, với mọi số h và k, ta có: bất kì, với mọi số h và k, ta có: |
| Hoạt động 3 | Tìm vectơ đối của các vectơ 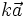 và và 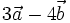 . . |
Trung điểm của đoạn thẳng và trọng tâm của tam giác[sửa]
a) Nếu I là trung điểm của đoạn thẳng AB thì với mọi điểm M ta có 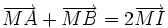 .
.
b) Nếu G là trọng tâm của tam giác ABC thì với mọi điểm M ta có 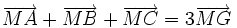 .
.
| Hoạt động 4 | Hãy sử dụng mục 5 của §2 để chứng minh các khẳng định trên. |
Điều kiện để hai vectơ cùng phương[sửa]
| Hoạt động 5 |  Hình 13p3 Cho các vectơ Hình 13p3 Cho các vectơ 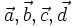 và và 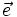 (hình 13p3). Tìm x, y, z biết: (hình 13p3). Tìm x, y, z biết: 1) 2) 3) |
Tổng quát, ta có:
Điều kiện cần và đủ để hai vectơ và
và 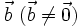 cùng phương là có một số k để
cùng phương là có một số k để 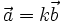 .
. CHỨNG MINH
- Thuận: giả sử
 và
và  cùng phương.
cùng phương.
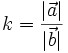 nếu
nếu  và
và  cùng hướng Lấy
cùng hướng Lấy 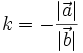 nếu
nếu  và
và  ngược hướng.
ngược hướng. Khi đó, theo định nghĩa ta có 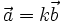 .
.
- Đảo: nếu
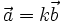 thì hai vectơ
thì hai vectơ  và
và  cùng phương.
cùng phương.
NHẬN XÉT:
Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để 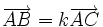 .
.
Phân tích một vectơ theo hai vectơ không cùng phương[sửa]
| Hoạt động 6 | Cho các vectơ 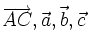 (hình 13p4). (hình 13p4). 1) Hãy vẽ vectơ 2) Hãy vẽ vectơ 3) Hãy vẽ vectơ |
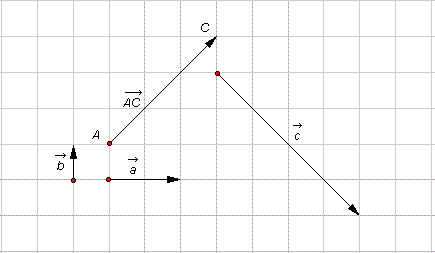 Hình 13p4
Hình 13p4 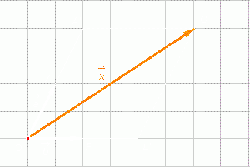
Tổng quát, ta có:
Cho hai vectơ và
và  không cùng phương. Khi đó mọi vectơ
không cùng phương. Khi đó mọi vectơ 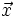 đều phân tích được một cách duy nhất theo hai vectơ
đều phân tích được một cách duy nhất theo hai vectơ  và
và  , nghĩa là có duy nhất cặp số h, k sao cho
, nghĩa là có duy nhất cặp số h, k sao cho 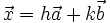 .
. CHỨNG MINH
- Vẽ
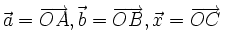 (hình 1-14).
(hình 1-14). - Kẻ CA' // OB và CB' // OA.
- Từ (2) suy ra, tứ giác OA'CB' là hình bình hành.
- Từ (3) và (1) suy ra,
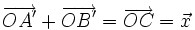 .
. - Vì
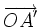 và
và  cùng phương nên có một số h để
cùng phương nên có một số h để 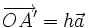 .
. - Vì
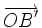 và
và  cùng phương nên có một số k để
cùng phương nên có một số k để 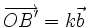 .
. - Từ (4), (5) và (6) suy ra:
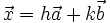 (đpcm).
(đpcm).
| VÍ DỤ 2 | 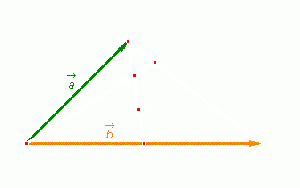 Cho tam giác ABC với trọng tâm G. Gọi I là trung điểm của đoạn thẳng AG và K là điểm trên cạnh AB sao cho a) Hãy phân tích 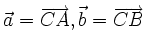 . . b) Chứng minh ba điểm C, I, K thẳng hàng. |
| Lời giải | a) Gọi AD là trung tuyến của tam giác ABC (hình 1-15). Ta có: 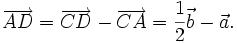 Do đó: 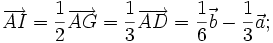 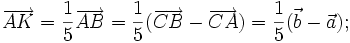 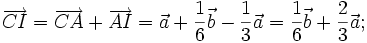 _____________(1*) _____________(1*) 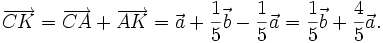 ___________(2*) ___________(2*) b) Từ (1*) và (2*), ta có |
BÀI TẬP[sửa]
1) Cho hình bình hành ABCD. Chứng minh rằng: 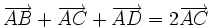 .
.
2)
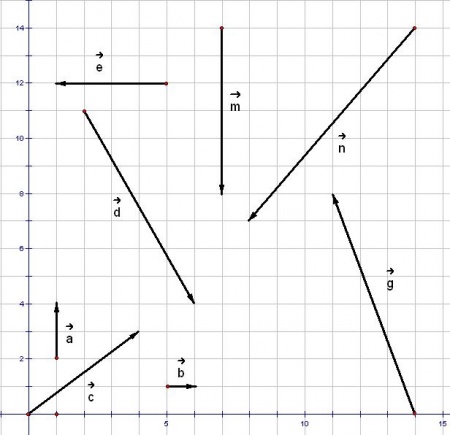
Cho các vectơ 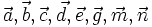 (hình 1-15p). Tìm k, h sao cho:
(hình 1-15p). Tìm k, h sao cho:
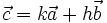 b)
b) 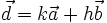 c)
c) 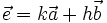 d)
d) 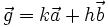 e)
e) 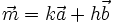 f)
f) 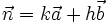
3) Cho AK và BM là hai trung tuyến của tam giác ABC. Hãy phân tích các vectơ 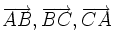 theo hai vectơ
theo hai vectơ 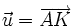 và
và 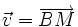 .
.
4) Trên đường thẳng chứa cạnh BC của tam giác ABC lấy một điểm M sao cho 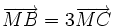 . Hãy phân tích vectơ
. Hãy phân tích vectơ 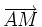 theo hai vectơ
theo hai vectơ 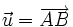 và
và 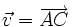 .
.
5) Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM. Chứng minh rằng:
a)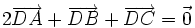 . b)
. b) 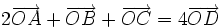 , với O là điểm tùy ý.
, với O là điểm tùy ý. 6) Gọi M và N lần lượt là trung điểm các cạnh AB và CD của tứ giác ABCD. Chứng minh rằng: 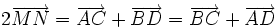 .
.
7) Cho hai điểm phân biệt A và B. Tìm điểm K sao cho 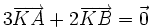
8) Cho tam giác ABC. Tìm điểm M sao cho 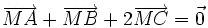 .
.
9) Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
10) Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng: 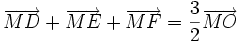 .
.
<<< Hình học 10
Liên kết đến đây
- Hình học 10
- Hình học 10/Chương I/§4. Hệ trục tọa độ
- Thành viên:Nguyenthephuc/Note: Đang viết
- Phân phối chương trình môn Toán lớp 10, Trung học phổ thông, Năm học 2006 - 2007


 Thể loại:
Thể loại: - Sách giáo khoa
- Hình học 10
 Kỹ thuật đặt câu hỏi Socratesửa đổi 7 tháng trước
Kỹ thuật đặt câu hỏi Socratesửa đổi 7 tháng trước 
 Kỹ thuật đặt câu hỏisửa đổi 7 tháng trước
Kỹ thuật đặt câu hỏisửa đổi 7 tháng trước 
 Nguyenthephuc/Note: Học làm cha, l…sửa đổi 7 tháng trước
Nguyenthephuc/Note: Học làm cha, l…sửa đổi 7 tháng trước 
 Nguyenthephuc/Note: Học làm cha, l…sửa đổi 7 tháng trước
Nguyenthephuc/Note: Học làm cha, l…sửa đổi 7 tháng trước 
 Nguyenthephuc/Note: Lượng hóa levelsbình luận 7 tháng trước
Nguyenthephuc/Note: Lượng hóa levelsbình luận 7 tháng trước 
Nhập email của bạn:
Cung cấp bởi Google
Trình đơn chuyển hướng
Công cụ cá nhân
- Mở tài khoản
- Đăng nhập
Không gian tên
- Nội dung
- Thảo luận
Biến thể
Tìm kiếm
Xem nhanh
- Trang Chính
- Tin tức Khoa học
- Tủ sách VLOS
- Giới thiệu Sách
- Quy trình Công nghệ
- Giáo án Điện tử
- Bài giảng Trực tuyến
- Ngân hàng Ý tưởng
- Ghi chú Khoa học
Cộng đồng
- Hỏi - Đáp
- Thảo luận mới
- Bài viết mới nhất
- Bài nhiều người đọc
- Hoạt động thành viên
- Thay đổi gần đây
Các đề án
- Sách giáo khoa mở
- Điện từ Sinh học
- Từ điển Thuốc
- Công nghệ Ưu tiên
- Văn hóa Khoa học
- Ngôn ngữ học
- Từ điển Hàn lâm
- Thần kinh & tư duy
- Các câu lạc bộ
- Sinh học đại cương
- Rùa Hồ Gươm
- Khái niệm Sinh học
Hướng dẫn để
- sơ cứu cấp cứu
- chăm sóc sức khỏe
- cân bằng tâm lý
- phát triển kỹ năng
- thay đổi lối sống
- giao tiếp xã hội
- phát triển tình yêu
- thủ thuật internet
- làm đẹp
- vệ sinh cá nhân
- ăn kiêng
- nấu ăn ngon
- làm mẹ chăm con
- làm vườn trồng cây
- hạnh phúc gia đình
Công cụ
- Các liên kết đến đây
- Thay đổi liên quan
- Các trang đặc biệt
- Bản để in
- Liên kết thường trực
- Thông tin trang
Từ khóa » định Lý Trọng Tâm Vecto
-
Bài Tập Về Quy Tắc Trọng Tâm Tam Giác Của Vecto Cực Hay, Chi Tiết
-
Quy Tắc Trung điểm Vecto, Trọng Tâm, Quy Tắc Hình Bình Hành Lớp 10 ...
-
Bài Tập Về Quy Tắc Trọng Tâm Tam Giác Của Vecto Cực Hay, Chi Tiết
-
Trọng Tâm Của Tam Giác - Thayphu
-
Lý Thuyết Tổng Của Hai Véc Tơ Toán 10
-
Trọng Tâm Là Gì? Công Thức Tính Trọng Tâm Của Tam Giác
-
Một Số Công Thức Về Véc Tơ Lớp 10
-
Mở Rộng Công Thức Vectơ Về Trọng Tâm Tam Giác Và ứng Dụng - 123doc
-
Chuyên đề Cách Tìm Tọa độ Trọng Tâm Tam Giác - DINHNGHIA.VN
-
(PDF) Vectơ Và Các Phép Toán | Ngốc Sam
-
Lý Thuyết Các Hệ Thức Lượng Trong Tam Giác Và Giải Tam Giác
-
Trọng Tâm Tam Giác: Khái Niệm, Tính Chất Và Cách Xác định - Thợ Sửa Xe
-
Vectơ – Wikipedia Tiếng Việt
-
Tìm Tọa độ Trọng Tâm Tam Giác Trong Mặt Phẳng Oxy
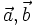 (hình 13p1).
(hình 13p1).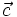 biết
biết 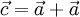 .
.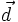 biết
biết 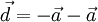 .
.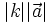 .
.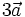 .
.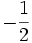 kí hiệu như thế nào? Vẽ vectơ đó.
kí hiệu như thế nào? Vẽ vectơ đó.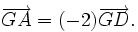
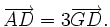
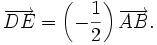
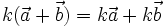
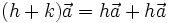
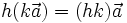
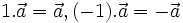
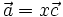
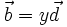
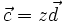 .
.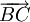 sao cho
sao cho 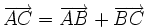 .
.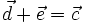 . Có bao nhiêu cặp vectơ
. Có bao nhiêu cặp vectơ 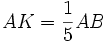 .
.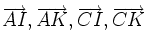 theo
theo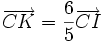 . Vậy ba điểm C, I, K thẳng hàng.
. Vậy ba điểm C, I, K thẳng hàng.