Khối Tròn Xoay – Wikipedia Tiếng Việt
Trong toán học, kỹ thuật, và sản xuất chế tạo, khối tròn xoay là một hình khối thu được bằng cách quay một đường cong phẳng xung quanh một đường thẳng (trục quay) nằm trên cùng mặt phẳng.
Giả sử đường cong không cắt trục quay, khi đó thể tích của khối tròn xoay bằng độ dài của đường tròn vẽ bởi trọng tâm của khối nhân với diện tích mặt tròn xoay (hay còn gọi là định lý trọng tâm Pappus).
Cách biểu diễn bằng đĩa là một nguyên tố thể tích (volume element) 3 chiều của khối tròn xoay. Nguyên tố được tạo bằng cách quay một đoạn thẳng (của độ dài w) quanh một trục (nằm cách xa r đơn vị), do vậy thể tích của hình trụ bằng πr2w đơn vị nó chứa.
Tìm thể tích
[sửa | sửa mã nguồn]Có hai phương pháp phổ biến nhằm tìm thể tích khối tròn xoay là phương pháp đĩa và phương pháp tích phân phân vỏ. Để áp dụng các phương pháp này, cách dễ nhất là vẽ đồ thị xác định đường cong; tìm diện tích nó chứa mà sẽ được quay quanh trục; sau đó xác định thể tích bằng nhát cắt dạng đĩa của khối, với độ dày bằng δx, hoặc bằng vỏ trụ với bề rộng δx; sau đó tìm giới hạn của tổng các nguyên tố thể tích này khi δx tiến tới 0, mà giá trị có thể tìm được bằng cách tính tích phân.
Phương pháp đĩa
[sửa | sửa mã nguồn]
Phương pháp đĩa được sử dụng khi nhát cắt vẽ ra vuông góc với trục quay; nghĩa là khi thực hiện tích phân song song với trục quay.
Thể tích của khối tròn xoay hình thành bằng cách quay miền diện tích giới hạn bởi các đường cong f(x) và g(x) và các đường thẳng x = a và x = b quanh trục x xác định bằng
Nếu g(x) = 0 (ví dụ xoay một đường cong quanh trục x), công thức thu gọn thành:
Có thể hình dung phương pháp này bằng cách coi một hình chữ nhật nhỏ nằm ngang ở tọa độ y giữa f(y) nằm trên và g(y) nằm ở dưới, và quay nó xung quanh trục y; khi đó nó tạo thành một vòng xuyến (hoặc đĩa trong trường hợp g(y) = 0), với bán kính ngoài bằng f(y) và bán kính trong bằng g(y). Diện tích của vòng bằng π(R2 − r2), với R là bán kính ngoài (trong trường hợp f(y)), và r là bán kính trong (trong trường hợp g(y)). Thể tích của mỗi đĩa vô cùng bé do đó bằng πf(y)2 dy. Giới hạn của tổng Riemann của thể tích các đĩa nằm giữa a và b trở thành tích phân (1).
Phương pháp hình trụ
[sửa | sửa mã nguồn] Bài chi tiết: Tích phân vỏ
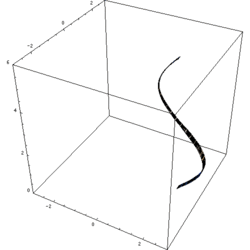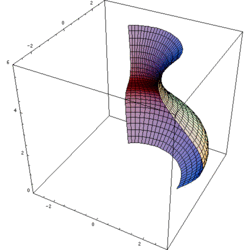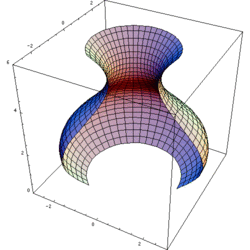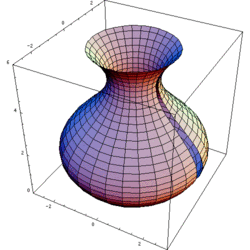
 The shapes at rest
The shapes at rest The shapes in motion, showing the solids of revolution formed by each
The shapes in motion, showing the solids of revolution formed by each Phương pháp hình trụ được sử dụng khi các khối nhát cắt được vẽ song song với trục quay; tức là thực hiện tích phân vuông góc với trục quay.
Thể tích khối tròn xoay nằm giữa các đường cong f(x) và g(x) và các đường thẳng x = a và x = b quay quanh trục y cho bởi
Nếu g(x) = 0 (ví dụ quay vùng diện tích giới hạn bởi đường cong và trục y), công thức trên trở thành:
Phương pháp này có thể hình dung bằng một hình chữ nhật theo phương đứng ở tọa độ x với chiều cao bằng f(x) − g(x), và quay xung quanh trục y; nó tạo thành cái vỏ hình trụ. Diện tích bề mặt của hình trụ bằng 2πrh, với r là bán kính (trong trường hợp x), và h là chiều cao (trong trường hợp f(x) − g(x)). Cộng tổng diện tích của mặt dọc theo tích phân thu được tổng thể tích khối tròn xoay.
Dạng tham số
[sửa | sửa mã nguồn]
Khi một đường cong được xác định bởi dạng phương trình tham số (x(t),y(t)) trên đoạn [a,b], thể tích của khối tròn xoay xác định bởi đường sinh quay quanh trục x hoặc trục y cho bởi:[1]
Trong một số trường hợp, diện tích mặt của khối tròn xoay tạo bởi đường sinh xung quanh trục x hoặc trục y cho bởi:[2]
Xem thêm
[sửa | sửa mã nguồn]- Sừng Gabriel
- Định lý Guldinus
- Giả mặt cầu (Pseudosphere)
- Mặt tròn xoay
- Múi (Ungula)
Chú thích
[sửa | sửa mã nguồn]- ^ Sharma, A. K. (2005). Application Of Integral Calculus. Discovery Publishing House. tr. 168. ISBN 81-7141-967-4.
- ^ Singh, Ravish R. (1993). Engineering Mathematics (ấn bản thứ 6). Tata McGraw-Hill. tr. 6.90. ISBN 0-07-014615-2.
Tham khảo
[sửa | sửa mã nguồn]- "Volumes of Solids of Revolution". CliffsNotes.com. ngày 12 tháng 4 năm 2011. Bản gốc lưu trữ 19 tháng 3 2012. Truy cập 26 tháng 1 2018. {{Chú thích web}}: Kiểm tra giá trị ngày tháng trong: |ngày truy cập= và |archive-date= (trợ giúp)
- Ayres, Frank; Mendelson, Elliott (2008). Calculus. Schaum's Outlines. McGraw-Hill Professional. tr. 244–248. ISBN 978-0-07-150861-2. (online copy, tr. 244, tại Google Books)
- Weisstein, Eric W., "Solid of Revolution" từ MathWorld.
| Cơ sở dữ liệu tiêu đề chuẩn |
|
|---|
Từ khóa » Sự Xoay Tròn Là Gì
-
Từ điển Việt Anh "xoay Tròn" - Là Gì?
-
Mặt Tròn Xoay – Wikipedia Tiếng Việt
-
Bài 1: Khái Niệm Về Mặt Tròn Xoay - Chương II - Hình Học Lớp 12
-
Bài 1: Khái Niệm Về Mặt Tròn Xoay - Hoc24
-
Từ điển Tiếng Việt - Từ Giũa Xoay Tròn Là Gì
-
Xoay Là Gì, Nghĩa Của Từ Xoay | Từ điển Việt
-
được Gọi Là Trục Của Mặt Tròn Xoay. - SureTEST
-
Lý Thuyết Khái Niệm Về Mặt Tròn Xoay | SGK Toán Lớp 12
-
Sự Khác Biệt Giữa Xoay Và Xoay







