Mặt Tròn Xoay – Wikipedia Tiếng Việt

Một mặt tròn xoay là một bề mặt trong không gian Euclid tạo bằng cách quay một đường cong (đường sinh) xung quanh một trục cố định.[1]

Ví dụ các mặt tròn xoay tạo từ một đường thẳng bao gồm hình trụ tròn và mặt nón phụ thuộc vào đường thẳng đó có song song với trục quay hay không. Khi quay một đường tròn xung quanh một đường kính của nó thu được một mặt cầu mà đường tròn chính là đường tròn lớn của nó, và nếu quay đường tròn xung quanh một trục nằm bên ngoài nó thì sẽ thu được mặt xuyến không tự cắt chính nó (hay còn gọi là vòng xuyến).

Các tính chất

[sửa | sửa mã nguồn]

Giao tuyến của mặt phẳng đi qua trục quay của mặt tròn xoay gọi là tiết diện kinh tuyến (meridional sections). Bất kỳ tiết diện kinh tuyến nào cũng được coi là phần tử sinh trong mặt phẳng xác định bởi tiết diện và trục quay.[2]

Giao tuyến của mặt phẳng vuông góc với trục quay và mặt tròn xoay là các đường tròn.

Một số trường hợp đặc biệt như hypeboloit (hyperboloid) (một phần hay hai phần) và elip paraboloit (elliptic paraboloid) là những mặt tròn xoay. Đây là những mặt bậc hai mà tiết diện vuông góc với trục quay là đường tròn.

Công thức tính diện tích

[sửa | sửa mã nguồn]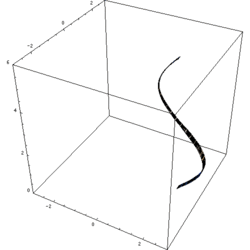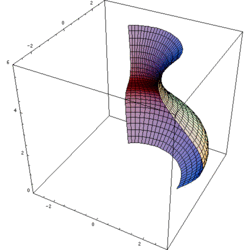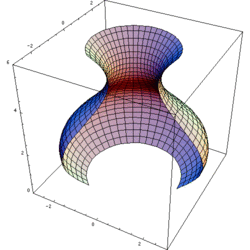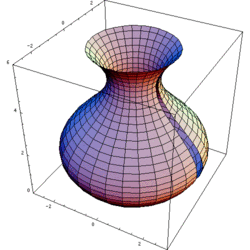

Nếu một đường cong xác định bằng phương trình tham số x(t), y(t), với t xác định trên đoạn [a,b], và trục tròn xoay là trục y, thì diện tích của mặt Ay xác định bằng tích phân

A y = 2 π ∫ a b x ( t ) ( d x d t ) 2 + ( d y d t ) 2 d t , {\displaystyle A_{y}=2\pi \int _{a}^{b}x(t)\,{\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}\,dt,}

cho thấy x(t) luôn không âm giữa hai điểm a and b. Công thức này có dạng tương đương với định lý trọng tâm Pappus (Pappus's centroid theorem).[3] Đại lượng

( d x d t ) 2 + ( d y d t ) 2 {\displaystyle {\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}}

xuất phát từ định lý Pythagore và đại diện cho một đoạn nhỏ của cung của đường cong, giống như trong công thức độ dài cung. Đại lượng 2πx(t) là quỹ đạo của trọng tâm của đoạn nhỏ này, như đòi hỏi bởi định lý Pappus.

Tương tự, khi trục quay là trục x và cho thấy hàm y(t) luôn không âm, diện tích mặt tròn xoay được tính bằng[4]

A x = 2 π ∫ a b y ( t ) ( d x d t ) 2 + ( d y d t ) 2 d t . {\displaystyle A_{x}=2\pi \int _{a}^{b}y(t)\,{\sqrt {\left({dx \over dt}\right)^{2}+\left({dy \over dt}\right)^{2}}}\,dt.}

Nếu đường cong được miêu tả bằng hàm y = f(x), a ≤ x ≤ b, thì tích phân trở thành

A x = 2 π ∫ a b y 1 + ( d y d x ) 2 d x = 2 π ∫ a b f ( x ) 1 + ( f ′ ( x ) ) 2 d x {\displaystyle A_{x}=2\pi \int _{a}^{b}y{\sqrt {1+\left({\frac {dy}{dx}}\right)^{2}}}\,dx=2\pi \int _{a}^{b}f(x){\sqrt {1+{\big (}f'(x){\big )}^{2}}}\,dx}

đối với trục xoay là trục x và

A y = 2 π ∫ a b x 1 + ( d x d y ) 2 d y {\displaystyle A_{y}=2\pi \int _{a}^{b}x{\sqrt {1+\left({\frac {dx}{dy}}\right)^{2}}}\,dy}

đối với trục xoay là trục y (sử dụng a ≤ y ≤ b). Các công thức này được rút ra từ công thức ở trên.

Ví dụ, mặt cầu bán kính đơn vị có đường sinh là đường cong xác định bởi tham số y(t) = sin(t), x(t) = cos(t), khi t thuộc đoạn [0,π]. Diện tích bề mặt của nó bằng

A = 2 π ∫ 0 π sin ⁡ ( t ) ( cos ⁡ ( t ) ) 2 + ( sin ⁡ ( t ) ) 2 d t = 2 π ∫ 0 π sin ⁡ ( t ) d t = 4 π . {\displaystyle {\begin{aligned}A&{}=2\pi \int _{0}^{\pi }\sin(t){\sqrt {{\big (}\cos(t){\big )}^{2}+{\big (}\sin(t){\big )}^{2}}}\,dt\\&{}=2\pi \int _{0}^{\pi }\sin(t)\,dt\\&{}=4\pi .\end{aligned}}}

Đối với trường hợp mặt cầu bán kính r, phương trình đường cong y(x) = √r2 − x2 quay xung quanh trục x

A = 2 π ∫ − r r r 2 − x 2 1 + x 2 r 2 − x 2 d x = 2 π r ∫ − r r r 2 − x 2 1 r 2 − x 2 d x = 2 π r ∫ − r r d x = 4 π r 2 {\displaystyle {\begin{aligned}A&{}=2\pi \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,{\sqrt {1+{\frac {x^{2}}{r^{2}-x^{2}}}}}\,dx\\&{}=2\pi r\int _{-r}^{r}\,{\sqrt {r^{2}-x^{2}}}\,{\sqrt {\frac {1}{r^{2}-x^{2}}}}\,dx\\&{}=2\pi r\int _{-r}^{r}\,dx\\&{}=4\pi r^{2}\,\end{aligned}}}

Mặt tròn xoay cực tiểu là mặt tròn xoay của đường cong đi qua hai điểm cho trước mà diện tích bề mặt của nó là cực tiểu.[5] Một vấn đề cơ bản trong phép tính biến phân đó là tìm đường cong giữa hai điểm cho trước mà tạo ra mặt tròn xoay cực tiểu.[5]

Chỉ tồn tại có hai mặt tròn xoay cực tiểu đó là mặt phẳng và mặt catinoit (catenoid, mặt có đường sinh là đường dây xích (catenary)).[6]

Quay một hàm số

[sửa | sửa mã nguồn]

Để tạo ra một mặt tròn xoay từ hàm số y = f(x), thực hiện bằng cách tham số hóa u hàm số đó, và đặt trục quay của hàm số là trục u, sau đó sử dụng v để quay hàm xung quanh trục bằng cách đặt hai hàm số khác bằng f(u) sin v và f(u) cos v. Ví dụ, để quay hàm số y = f(x) xung quanh trục x bắt đầu từ phía trên mặt phẳng xz, viết tham số hóa của nó bằng

r → ( u , v ) = ⟨ u , f ( u ) sin ⁡ v , f ( u ) cos ⁡ v ⟩ {\displaystyle {\vec {r}}(u,v)=\langle u,f(u)\sin v,f(u)\cos v\rangle }

với u = x and v ∈ [0,2π].

Đường trắc địa trên một mặt tròn xoay

[sửa | sửa mã nguồn]

Kinh tuyến trên mặt tròn xoay luôn luôn là đường trắc địa của mặt này. Các đường trắc địa khác bị chi phối bởi liên hệ Clairaut.[7]

Hình phỏng xuyến

[sửa | sửa mã nguồn] Bài chi tiết: Hình phỏng xuyến

Một mặt tròn xoay có lỗ ở bên trong và trục xoay không cắt bề mặt của nó, được gọi là hình phỏng xuyến (toroid).[8] Ví dụ, khi quay một hình chữ nhật quanh một trục song song với 1 cạnh của nó thì sẽ thu được hình phỏng xuyến có tiết diện là hình chữ nhật. Nếu xoay một đường tròn, thì sẽ thu được hình xuyến (torus).

Ứng dụng của mặt tròn xoay

[sửa | sửa mã nguồn]

Mặt tròn xoay và các tính chất của nó được ứng dụng trong nhiều lĩnh vực vật lý và kỹ thuật. Khi một đối tượng hình học được thiết kế bằng máy tính, từ các mặt tròn xoay có thể xác định được diện tích bề mặt mà không cần sử dụng đến đo độ dài và bán kính của vật được thiết kế.

Xem thêm

[sửa | sửa mã nguồn]

• Mặt kênh (Channel surface, một dạng tổng quát hóa của mặt tròn xoay)
• Sừng Gabriel
• Mặt Liouville, một mặt tổng quát hóa khác của mặt tròn xoay
• Khối tròn xoay
• Tích phân mặt
• Helicoit tổng quát (Generalized helicoid)

Tham khảo

[sửa | sửa mã nguồn]

1. ^ Middlemiss; Marks; Smart. “15-4. Surfaces of Revolution”. Analytic Geometry (ấn bản thứ 3). tr. 378. LCCN 68015472.
2. ^ Wilson, W.A.; Tracey, J.I. (1925), Analytic Geometry , D.C. Heath and Co., tr. 227
3. ^ Thomas, George B. “6.7: Area of a Surface of Revolution; 6.11: The Theorems of Pappus”. Calculus (ấn bản thứ 3). tr. 206–209, 217–219. LCCN 69016407.
4. ^ Singh, R.R. (1993). Engineering Mathematics (ấn bản thứ 6). Tata McGraw-Hill. tr. 6.90. ISBN 0-07-014615-2.
5. ^ a b Weisstein, Eric W., "Minimal Surface of Revolution" từ MathWorld.
6. ^ Weisstein, Eric W., "Catenoid" từ MathWorld.
7. ^ Pressley, Andrew. "Chapter 9 - Geodesics." Elementary Differential Geometry, 2nd ed., Springer, London, 2012, pp. 227–230.
8. ^ Weisstein, Eric W., "Toroid" từ MathWorld.

Liên kết ngoài

[sửa | sửa mã nguồn]

• Weisstein, Eric W., "Surface of Revolution" từ MathWorld.
• “Surface de révolution”. Encyclopédie des Formes Mathématiques Remarquables (bằng tiếng Pháp).