Mặt Bậc Hai – Wikipedia Tiếng Việt

Bước tới nội dung

Nội dung

chuyển sang thanh bên ẩn

• Đầu
• 1 Các loại mặt bậc hai cơ bản
• 2 Tổng quát
• 3 Xem thêm
• 4 Tham khảo
• 5 Liên kết ngoài

• Bài viết
• Thảo luận

Tiếng Việt

• Đọc
• Sửa đổi
• Sửa mã nguồn
• Xem lịch sử

Công cụ Công cụ chuyển sang thanh bên ẩn Tác vụ

• Đọc
• Sửa đổi
• Sửa mã nguồn
• Xem lịch sử

Chung

• Các liên kết đến đây
• Thay đổi liên quan
• Trang đặc biệt
• Liên kết thường trực
• Thông tin trang
• Trích dẫn trang này
• Lấy URL ngắn gọn
• Tải mã QR

In và xuất

• Tạo một quyển sách
• Tải dưới dạng PDF
• Bản để in ra

Tại dự án khác

• Wikimedia Commons
• Khoản mục Wikidata

Giao diện chuyển sang thanh bên ẩn Bách khoa toàn thư mở Wikipedia

Mặt bậc hai hay mặt cong bậc hai là mặt trong không gian affine ba chiều, quỹ tích những điểm thỏa mãn phương trình bậc hai dạng a 11 . x 2 + a 22 . y 2 + a 33 . z 2 + a 12 . x y + a 13 . x z + a 23 . y z + a 14 . x + a 24 . y + a 34 . z + a 44 = 0 {\displaystyle a_{11}.x^{2}+a_{22}.y^{2}+a_{33}.z^{2}+a_{12}.xy+a_{13}.xz+a_{23}.yz+a_{14}.x+a_{24}.y+a_{34}.z+a_{44}=0}

Trong đó:

• A = ( a i j ) {\displaystyle A=(a_{ij})} là ma trận thực đối xứng, tức là a i j = a j i {\displaystyle a_{ij}=a_{ji}} .
• Phần bậc 2 được gọi là phần toàn phương
• Phần bậc 1 được gọi là phần tuyến tính
• a 44 {\displaystyle a_{44}} là phần hệ số tự do.

Các loại mặt bậc hai cơ bản

[sửa | sửa mã nguồn]

Mặt trụ
Mặt trụ elliptic thực	x 2 a 2 + y 2 b 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}
Mặt trụ elliptic ảo
Mặt trụ tròn xoay	x 2 a 2 + y 2 a 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1\,}
Mặt trụ parabolic	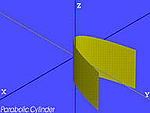x 2 + 2 a y = 0 {\displaystyle x^{2}+2ay=0\,}
Mặt trụ hyperbolic	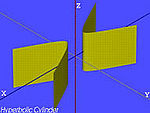x 2 a 2 − y 2 b 2 = 1 {\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,}
Mặt nón
Mặt nón elliptic thực	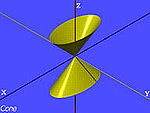x 2 a 2 + y 2 b 2 − z 2 c 2 = 0 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=0\,}
Mặt nón ảo	x 2 a 2 + y 2 b 2 + z 2 c 2 = 0 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=0\,}
Mặt Ellipsoid Bài chi tiết: Ellipsoid
Mặt Ellipsoid thực	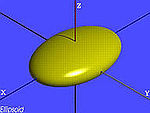x 2 a 2 + y 2 b 2 + z 2 c 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1\,}
Mặt cầu là mặt ellipsoid với ba trục bằng nhau a = b = c
Mặt Ellipsoid ảo	x 2 a 2 + y 2 b 2 + z 2 c 2 = − 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=-1\,}
Mặt Hyperboloid
Mặt Hyperboloid một tầng	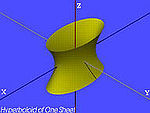x 2 a 2 + y 2 b 2 − z 2 c 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=1\,}
Mặt Hyperboloid hai tầng	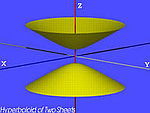x 2 a 2 + y 2 b 2 − z 2 c 2 = − 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-{z^{2} \over c^{2}}=-1\,}
Mặt hyperbolic paraboloid	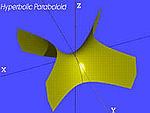x 2 a 2 − y 2 b 2 − z = 0 {\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}-z=0\,}
Mặt elliptic paraboloid	x 2 a 2 + y 2 b 2 − z = 0 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}-z=0\,}
Mặt elliptic paraboloid tròn xoay	x 2 a 2 + y 2 a 2 − z = 0 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}-z=0\,}
Cặp mặt phẳng thực và ảo liên hợp giao nhau
Cặp mặt phẳng thực và ảo liên hợp song song
Cặp mặt phẳng thực và ảo liên hợp trùng nhau

Tổng quát

[sửa | sửa mã nguồn]

Trong không gian xạ ảnh, mặt bậc hai là tập hợp những điểm { x 0 , x 1 , x 2 , … , x n } {\displaystyle \{x_{0},x_{1},x_{2},\ldots ,x_{n}\}} có tọa độ xạ ảnh thỏa mãn

∑ i , j = 0 n a i j x i x j + ∑ i = 0 n b i x i + R = 0 {\displaystyle \sum _{i,j=0}^{n}a_{ij}x_{i}x_{j}+\sum _{i=0}^{n}b_{i}x_{i}+R=0}

với ai,j không đồng thời bằng không. Với ai,j đồng thời bằng không, ta có mặt bậc hai suy biến thành mặt phẳng trong không gian metric n chiều.

Xem thêm

[sửa | sửa mã nguồn]

• Mặt phẳng
• Mặt tròn xoay
• Mặt bậc ba
• Mặt bậc bốn
• Mặt cong
• Mặt lồi
• Mặt liên tục
• Phương trình bậc hai

Tham khảo

[sửa | sửa mã nguồn]

Liên kết ngoài

[sửa | sửa mã nguồn] Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Mặt bậc hai.

• Interactive Java 3D models of all quadric surfaces Lưu trữ 2007-09-29 tại Wayback Machine
• Weisstein, Eric W., "Quadric", MathWorld.
• Quadric surface (mathematics) tại Encyclopædia Britannica (tiếng Anh)
• Mặt bậc hai tại Từ điển bách khoa Việt Nam

Các chủ đề chính trong toán học
Nền tảng toán học | Đại số | Giải tích | Hình học | Lý thuyết số | Toán học rời rạc | Toán học ứng dụng | Toán học giải trí | Toán học tô pô | Xác suất thống kê

Lấy từ “https://vi.wikipedia.org/w/index.php?title=Mặt_bậc_hai&oldid=71879411” Thể loại:

• Mặt bậc hai
• Hình học giải tích
• Hình học afin
• Quỹ tích
• Lý thuyết tập hợp
• Phương trình đại số

Thể loại ẩn:

• Bản mẫu webarchive dùng liên kết wayback