Mặt Trụ – Wikipedia Tiếng Việt

Trang chủ » Trụ Ellipse » Mặt Trụ – Wikipedia Tiếng Việt

Có thể bạn quan tâm

Mặt trụ là mặt tạo bởi một đường thẳng l giữ nguyên phương và di chuyển sao cho luôn luôn song song với chính nó, tựa trên một đường cong ω không đồng phẳng với l.

Đường ω gọi là đường tựa, đường thẳng l gọi là đường sinh của mặt trụ.

Khi đường tựa ω là một đường đơn phẳng khép kín, ta có mặt lăng trụ.

Các loại mặt trụ

[sửa | sửa mã nguồn]

Tùy theo bậc của đường cong ω mà người ta gọi bậc của mặt trụ. Với ω là đường cong bậc hai thì ta có mặt trụ bậc hai. Xem thêm mặt bậc hai

Nếu đường tựa của MT là elip, parabôn hay hypebôn thì MT được gọi là mặt trụ eliptic, parabôlic hay hypebôlic. Nếu đường tựa là một vòng tròn có mặt phẳng vuông góc với l thì ta có mặt trụ tròn xoay

Mặt trụ elliptic thực x 2 a 2 + y 2 b 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}=1\,}
Mặt trụ elliptic ảo
Mặt trụ tròn xoay x 2 a 2 + y 2 a 2 = 1 {\displaystyle {x^{2} \over a^{2}}+{y^{2} \over a^{2}}=1\,}
Mặt trụ parabolic 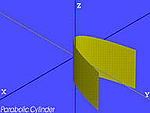x 2 + 2 a y = 0 {\displaystyle x^{2}+2ay=0\,}
Mặt trụ hyperbolic 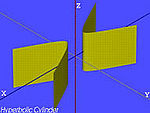x 2 a 2 − y 2 b 2 = 1 {\displaystyle {x^{2} \over a^{2}}-{y^{2} \over b^{2}}=1\,}

Định nghĩa trong giải tích

[sửa | sửa mã nguồn]

Xem thêm

[sửa | sửa mã nguồn]
  • Mặt nón
  • Mặt ellipsoid
  • Mặt siêu trụ
  • Hình trụ
  • Mặt bậc hai
  • Mặt tròn xoay

Tham khảo

[sửa | sửa mã nguồn]

Liên kết ngoài

[sửa | sửa mã nguồn] Wikimedia Commons có thêm hình ảnh và phương tiện truyền tải về Mặt trụ.
Hình tượng sơ khai Bài viết liên quan đến toán học này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn.
  • x
  • t
  • s
Bài viết này vẫn còn sơ khai. Bạn có thể giúp Wikipedia mở rộng nội dung để bài được hoàn chỉnh hơn.
  • x
  • t
  • s

Từ khóa » Trụ Ellipse