Một Số Loại ứng Suất Phổ Biến Trong Cơ Khí

1/ Ứng suất uốn

Dầm là một chi tiết mang tải trọng với trục đặt nằm ngang. Những tải trọng như vậy tạo ra mômen uốn trên dầm, sinh ra ứng suất uốn. Ứng suất uốn là ứng suất pháp, là kéo hoặc nén. Ứng suất uốn cực đại trong mặt cắt ngang của dầm sẽ xuất hiện ở phần xa nhất tính từ trục trung hoà của mặt cắt. Tại điểm đó, công thức xác định ứng suất uốn:

Công thức xác định ứng suất uốn lớn nhất: =  M.c/I

Trong đó:

• M là độ lớn mômen uốn tại mặt cắt 
• I là mômen quán tính của mặt cắt ngang đối với trục trung hoà của nó
• c là khoảng cách từ trục trung hoà đến thớ ngoài cùng của mặt cắt ngang dầm.

Độ lớn của ứng suất uốn thay đổi tuyến tính trong mặt cắt ngang từ giá trị bằng không tại trục trung hoà đến giá trị ứng suất kéo lớn nhất về một phía của trục trung hoà, và ứng suất nén lớn nhất ở phía còn lại. Hình 3-16 chỉ ra phân bố ứng suất điển hình trong mặt cắt ngang của dầm. Lưu ý rằng phân bố ứng suất phụ thuộc vào hình dạng của mặt cắt ngang.

Chú ý rằng uốn dương xuất hiện khi khi kiểu võng của dầm là phần lõm ở bên trên, dẫn đến nén ở phần trên của mặt cắt ngang và kéo ở phần dưới. Ngược lại, uốn âm làm cho dầm bị lõm ở bên dưới

Công thức uốn được sử dụng khi thoả mãn những điều kiện sau:

1. Dầm cần phải chịu uốn thuần tuý. Ứng suất cắt bằng không hoặc không đáng kể. Không có tải dọc trục.
2. Dầm không bị vặn hoặc chịu tải trọng xoắn.
3. Vật liệu dầm cần tuân theo định luật Húc
4. Môđun đàn hồi của vật liệu là như nhau với cả kéo và nén.
5. Dầm là thẳng lúc đầu và có mặt cắt ngang không đổi.
6. Mọi mặt cắt ngang của dầm vẫn phẳng khi uốn
7. Không có phần nào của dầm bị hỏng do mất ổn định hoặc uốn cục bộ.

Nếu điều kiện 1 là không hoàn toàn phù hợp, bạn có thể tiếp tục tính toán bằng cách sử dụng phương pháp của ứng suất tổng hợp trình bày trong chương 4. Với đa số các dầm trong thực tế đều khá dài so với chiều cao của chúng, ứng suất cắt là đủ nhỏ để bỏ qua. Hơn nữa, ứng suất uốn lớn nhất xuất hiện tại những lớp ngoài cùng của mặt cắt dầm, là nơi mà ứng suất cắt bằng không. Một dầm với mặt cắt ngang thay đổi, sẽ không thoả mãn điều kiện 5, có thể tính toán bằng cách sử dụng hệ số tập trung ứng suất thảo luận ở phần sau của chương này.

Để thuận tiện cho thiết kế đưa ra thuật ngữ mômen chống uốn, S S = I/c (3-23)

Công thức tính ứng suất uốn sẽ trở thành: Ứng suất uốn = M/S (3-24)

Vì I và c là các đặc trưng hình học của mặt cắt ngang của dầm, nên S cũng vậy. Khi đó, trong thiết kế thường xác định được ứng suất thiết kế d và với mômen uốn đã biết, giải được S:

Mômen chống uốn yêu cầu S = M/d (3-25)

Kết quả này là giá trị yêu cầu của mômen chống uốn. Từ đó những kích thước yêu cầu của mặt cắt ngang của dầm có thể được xác định.

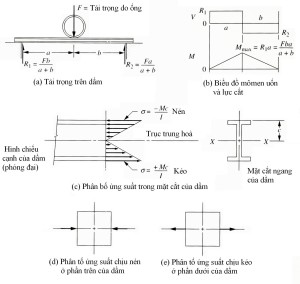
Ví dụ 3-12 Cho dầm trên hình 3-16, tải trọng F do ống là 12 000 lb. Các khoảng cách a = 4 ft và b = 6 ft. Xác định mômen chống uốn cần thiết của dầm để giới hạn ứng suất uốn ở 30 000 psi, ứng suất thiết kế đề nghị cho các kết cấu thép điển hình là uốn tĩnh.

Vấn đề: tính mômen chống uốn cần thiết S của dầm trong hình 3-16.

Đã cho: sự bố trí và sơ đồ tải được chỉ ra trong hình 3-16.

Chiều dài: chiều dài toàn bộ L = 10 ft; a = 4ft; b = 6 ft. Tải trọng F = 12 000 lb. Ứng suất thiết kế d = 30 000 psi

Tính toán: sử dụng công thức (3-25) để tính mômen chống uốn cần thiết S. Tính mômen uốn lớn nhất, xuất hiện tại điểm đặt tải trọng, sử dụng công thức trong hình 3-16(b).

Kết quả: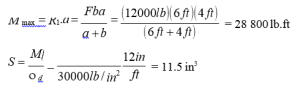

Nhận xét: bây giờ có thể chọn mặt cắt của dầm từ bảng A16-3 và A16-4, với S ít nhất cũng phải đạt giá trị trên. Mặt cắt thường được ưu tiên là dạng cánh rộng W8 15 với S = 11.8 in3

2/ Ứng suất cắt

Một dầm đỡ tải trọng, trục đặt nằm ngang sẽ chịu lực cắt, kí hiệu bằng V. Trong tính toán dầm, thường tính toán sự biến đổi lực cắt trên toàn bộ chiều dài của dầm và vẽ biểu đồ lực cắt. Sau đó tính ứng suất cắt từ

Ứng suất cắt đứng trong dầm: 

= VQ/I.t (3-16)

Trong đó:

1. I là mômen quán tính thẳng góc của mặt cắt ngang của dầm t là chiều dày của mặt cắt tại vị trí tính ứng suất
2. Q là mômen cấp 1, đối với trục trung hoà của diện tích phần mặt cắt ngang nằm về một phía đường ngang với điểm tính ứng suất. Để tính giá trị của Q dùng công thức sau,

Mômen cấp 1: Q = AP .y

Trong đó:

1. AP là diện tích mặt cắt bên trên điểm tính ứng suất
2. y là khoảng cách từ đường trung hoà của mặt cắt đến trọng tâm của diện tích

Trong một số sách hoặc tài liệu tham khảo, và trong những lần xuất bản trước đây của

quyển sách này, Q được gọi là mômen tĩnh. Ở đây chúng tôi sẽ sử dụng thuật ngữ mômen diện tích cấp một.

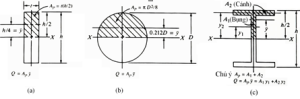Hình 3-13 Những minh hoạ về AP và y sử dụng để tính Q cho ba dạng mặt cắt

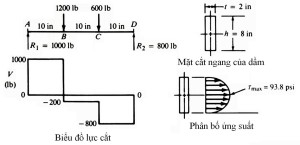
Hình 3-14 Biểu đồ lực cắt và ứng suất tiếp (cắt đứng) trong dầm

Với hầu hết các dạng mặt cắt, ứng suất cắt lớn nhất xuất hiện tại trục trọng tâm. Đặc biệt nếu chiều dày lớn hơn tại các vị trí cách xa trục trọng tâm, khi đó bảo đảm rằng giá trị lớn nhất của ứng suất cắt xuất hiện tại trục trọng tâm.

Hình 3-13 chỉ ra 3 ví dụ làm thế nào nào để tính Q với các mặt cắt ngang điển hình của dầm. Trong mỗi ví dụ, ứng suất cắt lớn nhất đều xuất hiện tại trục trung hoà.

Ví dụ 3-10 Hình 3-14 chỉ ra một dầm tựa đơn giản mang hai tải trọng tập trung. Biểu đồ lực cắt được vẽ ra, cùng với mặt cắt ngang hình chữ nhật và kích thước. Phân bố ứng suất là đường parabol, với ứng suất lớn nhất là tại đường trung hoà. Sử dụng công thức (3-16) để tính ứng suất cắt lớn nhất trong dầm

Nhận xét: Ứng suất cắt lớn nhất là 93.8 psi xuất hiện tại trục trung hoà của mặt cắt hình chữ nhật như trên hình 3-14. Phân bố ứng suất trong mặt cắt ngang là một đường parabol thông thường, kết thúc với ứng suất cắt bằng không tại mép trên và dưới. Đây là đặc trưng của ứng suất cắt tại mọi vị trí giữa gối đỡ bên trái tại A và điểm đặt tải 1200 lb tại B. Giá trị lớn nhất của ứng suất cắt tại một điểm bất kì trên dầm tỉ lệ với độ lớn của lực cắt tại điểm đó.

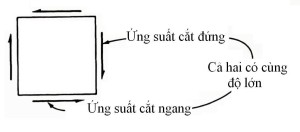
Chú ý rằng ứng suất cắt đứng bằng với ứng suất cắt ngang vì mọi phân tố của vật liệu chịu ứng suất cắt trên một mặt phải có ứng suất cắt với độ lớn tương tự trên mặt bên cạnh để phân tố cân bằng. Hình 3-15 chỉ ra hiện tượng này.

Trong hầu hết các dầm, độ lớn của ứng suất cắt hết sức nhỏ so với ứng suất uốn (xem mục phía sau). Với lí do này, nó thường không được tính đến. Một số trường hợp mà có ý nghĩa quan trọng là:

1. Khi vật liệu dầm có độ bền cắt tương đối nhỏ (ví dụ gỗ).
2. Khi mômen uốn bằng không hoặc nhỏ (và vì vậy ứng suất uốn nhỏ), ví dụ tại những các đầu của dầm tựa đơn giản và với những dầm ngắn.
3. Khi chiều dày của tiết diện chịu lực cắt là nhỏ, như những bộ phận làm từ tấm cán, một số dạng kéo, và bụng của những dạng kết cấu cán ví dụ như dầm cánh rộng

3/ Ứng suất xoắn

Khi xoắn, hoặc mômen xoắn, được đặt lên chi tiết, nó có xu hướng biến dạng do vặn, vì một phần của chi tiết bị xoay kéo theo các phần khác nữa.

Sự vặn như vậy gây ra ứng suất xoắn trong chi tiết. Với một phân tố nhỏ của chi tiết, bản chất của ứng suất này cũng giống như chịu ứng suất cắt trực tiếp. Tuy nhiên khi bị xoắn, phân bố của ứng suất không đồng đều trên mặt cắt ngang.

Đa phần các trường hợp thường xuyên chịu ứng suất xoắn trong thiết kế máy là các trục tròn truyền công suất.

Chương 12 bao gồm toàn bộ phần thiết kế trục.

 

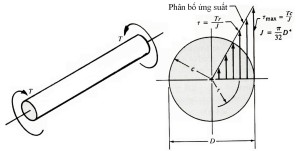
Hình 3-8 Phân bố ứng suất trong trục đặc

Công thức tính ứng suất xoắn

Khi chịu mômen xoắn, mặt ngoài của trục tròn đặc chịu biến dạng trượt lớn nhất và vì vậy ứng suất xoắn là lớn nhất. Xem hình 3-8. Giá trị lớn nhất của ứng suất xoắn được xác định theo:

Giá trị ứng suất xoắn lớn nhất trên trục tròn:

max = T.c/J (3-7)

Trong đó: c là bán kính mặt ngoài của trục J là mômen quán tính độc cực

Nhận xét: Ứng suất xoắn lớn nhất xuất hiện tại mặt ngoài trục trên toàn bộ chu vi của nó.

Nếu muốn tính ứng suất xoắn tại một số điểm trong trục, thường sử dụng công thức

Công thức chung tính ứng suất xoắn:  = T.r/J (3-8)

Trong đó r là bán kính từ tâm của trục đến điểm cần tính. Hình 3-8 chỉ ra đồ thị biến thiên tuyến tính của ứng suất xoắn từ 0 tại tâm của trục đến giá trị lớn nhất trên mặt ngoài trục.

Công thức (3-7) và (3-8) cũng dùng cho cả trục rỗng (hình 3-9 chỉ ra phân bố của ứng suất xoắn). Một lần nữa chú ý rằng ứng suất xoắn lớn nhất là tại mặt ngoài. Cũng cần lưu ý mặt cắt ngang đặc có mức ứng suất tương đối cao. Với cùng kết quả trục rỗng có hiệu quả hơn. Chú ý rằng lớp vật liệu gần tâm trục đặc chịu ứng suất không cao.

Để thuận tiện cho thiết kế, xác định môđun chống xoắn, ZP: Môđun chống xoắn ZP = J/c (3-9)

Khi đó công thức tính ứng suất xoắn lớn nhất là:

max = T/ZP (3-10)

Công thức tính môđun chống xoắn cũng được trình bày trong phụ lục 1. Dạng này của công thức rất hữu ích trong xác định ứng suất xoắn vì môđun chống xoắn chỉ là một thông số liên quan đến đặc trưng hình học của mặt cắt ngang.

4/ Ứng suất cắt trực tiếp

Ứng suất cắt trực tiếp xuất hiện khi lực tác dụng có xu hướng cắt qua chi tiết như cái kéo hoặc dao cắt hoặc khi chày và khuôn được dùng để đột một lỗ trên một tấm vật liệu.

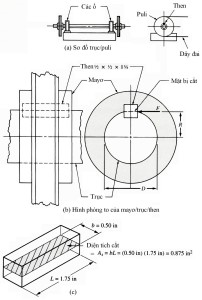
Một ví dụ quan trọng khác của cắt trực tiếp trong thiết kế máy là xu hướng then bị cắt đứt tại mặt cắt giữa trục và mayơ của chi tiết máy khi truyền mômen xoắn. Hình 3-7 chỉ ra tác động đó. Phương pháp tính ứng suất cắt trực tiếp tương tự với phương pháp đã dùng để tính ứng suất kéo thuần tuý vì lực tác dụng được giả thiết phân bố đều trên mặt cắt ngang chịu lực của chi tiết.

Nhưng loại ứng suất này là ứng suất tiếp khác với ứng suất pháp.

Kí hiệu sử dụng cho ứng suất cắt là chữ cái Hi Lạp tô (). Công thức tính ứng suất cắt được viết như sau

Ứng suất cắt trực tiếp  = lực cắt/ diện tích chịu cắt = F/AS

Ứng suất này được gọi một cách chính xác hơn là ứng suất cắt trung bình, nhưng để đơn giản chúng ta sẽ giả thiết là ứng suất phân bố đều trên diện tích cắt.

 

5/ Ứng suất pháp: kéo và nén

Ứng suất có thể được định nghĩa như là sức cản bên trong của một diện tích đơn vị của vật liệu ứng với tải trọng bên ngoài.

Ứng suất pháp có hai loại là kéo (dương) hoặc nén (âm).

Với các chi tiết mang tải mà tải trọng bên ngoài phân bố đều trên diện tích mặt cắt ngang của chi tiết, độ lớn của ứng suất có thể được tính từ công thức ứng suất pháp:

Kéo hoặc nén đúng tâm  = lực/diện tích = F/A

 

Các điều kiện để sử dụng công thức (3-1) là:

1. Bộ phận mang tải cần phải thẳng 2. Đường thẳng tác dụng của tải phải đi qua tâm mặt cắt ngang của chi tiết 3. Các mặt cắt của chi tiết phải đồng đều quanh vị trí tính ứng suất 4. Vật liệu phải đồng nhất và đẳng hướng 5. Trong trường hợp chi tiết chịu nén, nó phải ngắn để tránh mất ổn định. Điều kiện xảy ra mất ổn định được trình bày trong chương 6.

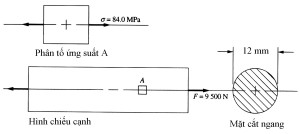
6/ Biểu diễn các ứng suất trên một phân tố ứng suất

Một mục tiêu quan trọng của phân tích ứng suất là xác định điểm trên chi tiết mang tải có mức ứng suất cao nhất.

Bạn sẽ phát triển khả năng xây dựng một phân tố ứng suất, một khối lập phương vô cùng nhỏ trong vùng ứng suất cao của chi tiết, và chỉ ra các véctơ biểu diễn cho những loại ứng suất tồn tại trên phân tố đó.

Sự định hướng của thành phần ứng suất có tính quyết định, và nó được hướng theo các trục đã xác định trên phân tố, thường gọi là x, y, và z.

Hình 3-5 chỉ ra 3 ví dụ của các phân tố ứng suất với ba loại ứng suất cơ bản là: kéo, nén và tiếp. Cả dạng khối lập phương hoàn chỉnh và dạng hình vuông đơn giản biểu diễn các phân tố ứng suất đều được chỉ ra.

Hình vuông là một mặt của khối lập phương trong mặt được chọn. Các hình vuông biểu diễn hình chiếu vuông góc các mặt của khối lập phương xuống mặt được chọn. Đầu tiên bạn cần lưu ý khi thể hiện khối lập phương và sau đó biểu diễn một phân tố ứng suất vuông chỉ ra ứng suất trên một mặt riêng mà bạn cần.

Trong một số trường hợp, với trạng thái ứng suất tổng quát hơn, có thể yêu cầu hai hoặc ba phân tố ứng suất vuông để mô tả một trạng thái ứng suất hoàn chỉnh.

Ứng suất kéo và nén, gọi là ứng suất pháp; tác dụng vuông góc với mặt đối diện của phân tố ứng suất. Ứng suất kéo có xu hướng kéo phân tố, trong khi ứng suất nén có xu hướng nén nó.

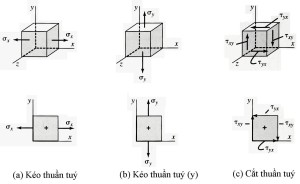
Hình 3-5 Các phân tố ứng suất của ba loại ứng suất

Ứng suất tiếp tạo ra bởi cắt trực tiếp, lực cắt trên dầm, hoặc xoắn.

Trong mỗi trường hợp, một phân tố chịu cắt có xu hướng bị cắt bởi một ứng suất hướng xuống trên một mặt đồng thời là một ứng suất hướng lên trên mặt đối diện song song.

Sự tác động như là một dụng cụ xén đơn giản hay cái kéo. Nhưng chú ý rằng nếu chỉ có một cặp ứng suất tiếp đối ứng tác động, phân tố ứng suất sẽ không cân bằng . Đúng hơn là phân tố có xu hướng quay vì cặp ứng suất tiếp tạo thành một ngẫu lực. Để tạo ra sự cân bằng, cần tồn tại một cặp ứng suất tiếp thứ hai trên hai mặt khác của phân tố, tác dụng theo hướng ngược với cặp đầu tiên.

Tóm lại, các ứng suất tiếp trên một phân tố sẽ thường được biểu diễn như hai cặp ứng suất bằng nhau tác dụng trên 4 mặt của phân tố. Hình 3-5(c) chỉ ra một ví dụ.

Kí hiệu qui ước cho ứng suất tiếp

1. Những ứng suất tiếp dương có xu hướng làm quay phân tố theo chiều kim đồng hồ.
2. Ứng suất tiếp âm có xu hướng làm quay phân tố theo hướng ngược chiều kim đồng hồ.
3. Hai chỉ số dưới được dùng để thể hiện ứng suất tiếp ở trong mặt nào.

Ứng suất của một chi tiết máy gây ra do lực và mômen quay tác động vào cấu kiện.

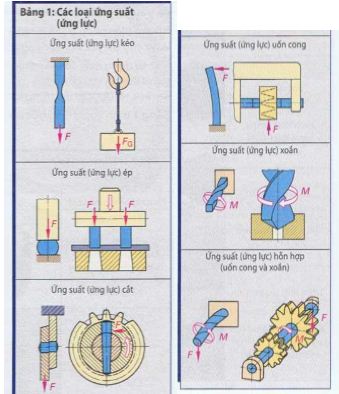
Ở những chi tiết thon, sự quẹo gập (oằn gấp, uốn dọc) thuộc vào loại ứng suất ép. Lúc oằn gấp bộ phận bị tác động ép tìm cách tránh qua hướng thẳng góc với hướng lực, thí dụ nhưchày mỏng của dụng cụ cắt.

Loại ứng suất trên bề mặt tiểp xúc của hai bộ phận ép vào nhau gọi là áp lực bề mặt, thí dụ như bạc bợ trục của một ổ trục bị ngõng trục quay ép vào bề mặt.

Nhiều khi trong một bộ phận máy xuất hiện đồng thời nhiều loại ứng suất. Thí dụ như cốt của hộp số cùng lúc bị tác động uốn cong và vặn. Những trường hợp như thế được gọi là ứng suất hỗn hợp. Tác động ứng lực tạo ra trong chi tiết một ứng suất, ứng suất tùy thuộc vào độ lớn của lực và tiết diện, ở các loại ứng suất uốn cong, oằn gấp và vặn còn thêm dạng của tiết diện chi tiết, ứng suất được chỉ định với đơn vị Newton trên milimét vuông (N/mm2).

Ứng suất làm cho một vật liệu bị gãy được gọi là độ bền của vật liệu đó.

Cho mỗi loại ứng suất (ứng lực) ta có một độ bền tương ứng, thí dụ độ bền kéo cho ứng suất (ứng lực) kéo, độ bền ép cho ứng suất (ứng lực) ép.

Các loại tải trọng

Lực tác động vào bộ phận máy có thé nhận những độ lớn khác nhau theo trình tự thời gian của chúng

Trong trường hợp tải trọng tĩnh (trường hợp tải trọng I), tác động lực vào bộ phận máy tăng lên và từ đó ứng suất tăng từ không đến trị số tối đa và sẽ không đổi.

Thí dụ: Tải trọng xoắn của trục truyền động một quạt máy lúc bật lên tăng từ không đến trị số tối đa và giữ không đổi.

Trong trường hợp tải trọng động, mức độ thay đổi lâu dài và có thể thay đổi cả hướng ứng suất (liên tục).

Trong trường hợp tải động ngưỡng (trường hợp tải trọng II) ứng suất lên xuống giữa không và trị số tối đa.

Thí dụ: ứng suất uốn cong trong một cò mổ xú páp của động cơ.

Trong trường hợp tải tuần hoàn hay tải đổi hướng (trường hợp tải trọng III) ứng suất luôn lên xuống giữa điểm dương cao nhất và điểm âm thấp nhất.

Thí dụ: ở một trục quay, ứng suất uốn cong có chứa ứng suất kéo và ứng suất nén thay đổi chiều trong mỗi nửa vòng quay.

Trong tải trọng động thông thường (tải động tổng quát) ứng suất lên xuống không đồng đều giữa một trị số cao và một trị số thấp (Hình 1)

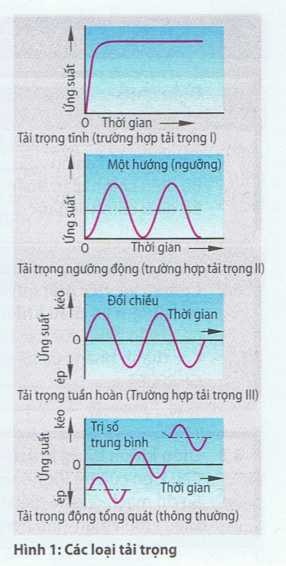
Thí dụ: Tải trọng xoắn do lực cắt thay đổi trong trục chính máy phay lúc phay chu vi.

Bộ phận máy chịu ứng suất (ứng lực) động làm cho vật liệu bị mỏi và tác dụng của rãnh khía có nguy cơ nhiều hơn tác động tĩnh. Vì lý do này mà độ bền mỏi (trang 298) thấp hơn độ bền của bộ phận bị ứng suất (ứng lực) tĩnh.

Hiệu ứng rãnh khía

Nếu trong chi tiết không có rãnh khía những đường lực phân phối đều thì ở chi tiết có rãnh khía chúng sẽ hội tụ trong vùng tiết diện của vị trí đường rãnh (Hình 2). Vì thế tải trọng trong phạm vi có rãnh lớn hơn rõ rệt.