Parabol Là Gì? Cách Lập Phương Trình Parabol Nhanh Nhất
Có thể bạn quan tâm
Toán học đại số luôn là bộ môn có rất nhiều thú vị, trong đó parabol có lẽ là nguyên nhân khiến nhiều học sinh phải đau đầu. Từ cách lập phương trình parabol cho tới cách vẽ và giải toán đều không đơn giản. Để giúp các bạn học sinh tự tin hơn với những bài toán về parabol, bài viết hôm nay LabVIETCHEM sẽ hướng dẫn các bạn cách lập phương trình nhanh nhất. Cùng dành ít phút theo dõi với chúng tôi nhé!
Mục lục- Khái niệm parabol là gì?
- Đường parabol có đặc điểm gì?
- Tổng quan phương trình parabol
- 1. Phương trình đường parabol dạng tổng quát
- 2. Phương trình đường parabol dạng chính tắc
- 3. Cách viết phương trình parabol
- ứng dụng của parabol trong đời sống là gì?
- 1. Hình parabol ứng dụng trong lĩnh vực xây dựng
- 2. Hình parabol ứng dụng trong chế tạo mặt kính
- 3. Ứng dụng chế tạo ăng ten hình parabol
Khái niệm parabol là gì?
Hình ảnh đường parabol cơ bản
Parabol được định nghĩa trong toán học là một đường conic (đường cong bậc 2) được sinh ra bởi giao của hình nón với mặt phẳng song song theo đường sinh của chính hình đó. Nói một cách khác thì parabol còn được hiểu là quỹ tích tập hợp tất cả các điểm cách đều một điểm cố định và một đường thẳng đã cho từ trước.
Trong một vài trường hợp đặc biệt, có thể xảy ra khi mặt phẳng cắt lại tiếp xúc với mặt conic thì giao tuyến sẽ suy biến thành đường thẳng. Vì thế mà parabol thực chất là một khái niệm khá trừu tượng trong lĩnh vực toán học. Ngoài lĩnh vực này, nó còn được ứng dụng rất nhiều trong vật lý, các mảng kỹ thuật khác.
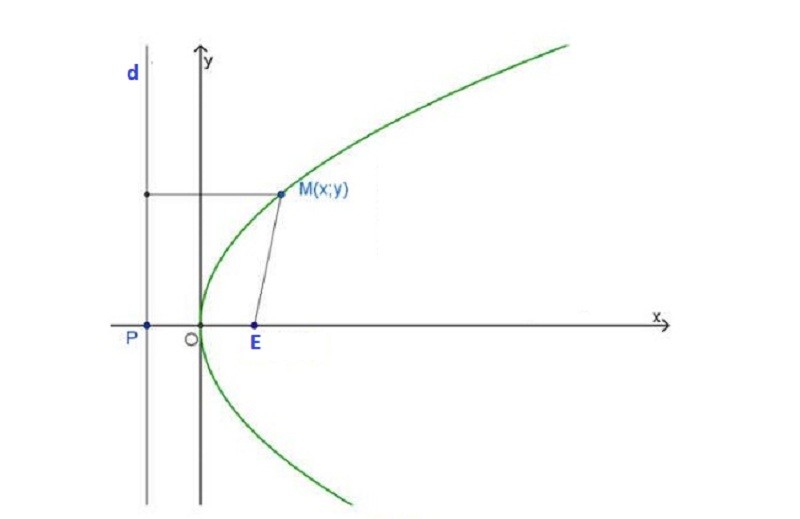
Ví dụ: Cho một điểm E cố định trước và 1 đường d không đi qua E. Khi đó đường parabol là đường cong bậc 2 tập hợp tất cả các điểm M cách đều cả E và đường thẳng d. Khi đó E được gọi là tiêu điểm; đường d là đường chuẩn; khoảng cách từ điểm E đến đường thẳng d được gọi là tham số tiêu. (như hình minh họa)
Đường parabol có đặc điểm gì?
Một đường parabol chỉ có duy nhất một trục đối xứng. Trục này sẽ đi qua tiêu điểm cố định và vuông góc với đường chuẩn. Giao điểm của đường chuẩn và parabol tại 1 điểm được gọi là đỉnh. Đường parabol chỉ quay xung quanh trực của chính nó trong không gian ba chiều.
Trong một vài trường hợp đường parabol được coi là một dạng elip với tiêu cự ở vô hạn; là ảnh nghịch đảo của một đường hình tim.
Tổng quan phương trình parabol
1. Phương trình đường parabol dạng tổng quát
y = a2 + bx + c
Trong đó:
Hoành độ của điểm đỉnh parabol là -b2a. Thay tọa độ hoành này vào phương trình tổng quát ta sẽ được công thức dạng :
y =( b2-4ac)/4a
2. Phương trình đường parabol dạng chính tắc
Cho đường parabol với tiêu điểm E cùng đường chuẩn d. Chọn hệ tọa độ Oxy, d giao với trục hoành tại P. Khi đó O là trung điểm của EP và E nằm trên trục ox. Từ đó ta có tọa độ của các điểm như sau:
F (p/2; 0) và P( -p/2; 0) ; d= x + p/2 = 0 (phương trình đường thẳng d)
Đường parabol là tập hợp các điểm M (x;y) trong đó khoảng cách ME chính là bằng khoảng cách từ M tới đường thẳng d. Ta suy ra được phương trình
√[(x-p/2)2 + y2]
y2 = 2px (ĐK: p>0)
3. Cách viết phương trình parabol
Cách viết phương trình parabol đơn giản
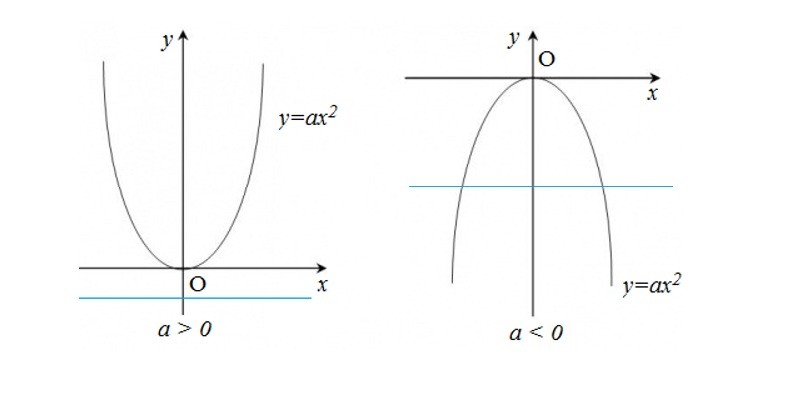
Giả sử cho hàm số y = ax2 . Hàm số được xác định trên tập R (tập số thực). Khi đó ta có:
- a>0 hàm số giảm trên miền (-∞ ; 0) và tăng trên miền (0;+ ∞ ), Min khi x=0
- a<0 hàm số tăng trên miền (-∞ ; 0) và giảm trên miền (0;+ ∞ ), Max khi x=0
Từ đó ta có đồ thị parabol của hàm số đã cho có đỉnh nằm tại gốc tọa độ O lấy trục Oy làm trục đối xứng. (theo hình minh họa).
Ứng dụng của parabol trong đời sống là gì?
1. Hình parabol ứng dụng trong lĩnh vực xây dựng

Các nhịp cầu được xây dựng theo hình parabol để giảm lực tác dụng
Trong xây dựng, khi người ta làm cầu có hình dạng đường cong parabol với các nhịp có bề lõm quay xuống dưới. Với kết cấu như vậy sẽ giúp giảm lực mà cây cầu phải gánh. Đồng thời lực tác động đến cầu sẽ được chia đều sang 2 bên. Giảm đi lực tác động thì cầu sẽ khó xảy ra tình trạng sập. Luôn duy trì được khoảng an toàn tốt. Trong trường hợp này thì dòng người, xe cộ lưu thông trên cầu sẽ theo hướng tiếp tuyến với mặt cầu. Càng làm cho lực tác dụng được giảm đi đáng kể.
Bên cạnh đó, hình parabol còn được ứng dụng trong xây dựng các trò vui chơi giải trí cảm giác mạnh tại công viên như: trò tàu lượn siêu tốc. Đường ray xe lửa được thiết kế theo cung đường parabol vừa có tác dụng tăng cảm giác mạnh lại giảm được động lực tác dụng khi tàu di chuyển.
2. Hình parabol ứng dụng trong chế tạo mặt kính
Những loại kính thiên văn phản xạ và gương cầu đều được chế tạo dưới dạng mặt lồi parabol. Điều này giúp các thiết bị có thể lan tỏa ánh sáng rộng hơn, xa hơn so với mặt phẳng thông thường. Giúp ích rất nhiều trong việc kiểm soát tầm nhìn của người đi đường khi quan sát.
3. Ứng dụng chế tạo ăng ten hình parabol

Ăng ten hình parabol thu phát nhiều kênh thông tin tốt hơn
Tương tự với gương cầu lồi thì ăng ten cũng vậy. Thay vì sử dụng mặt phẳng thì người ta sẽ chế tạo theo đường cong conic dạng parabol. Với mục đích để các loại sóng điện từ hội tụ tại một điểm trung tâm giúp thu phát được nhiều kênh thông tin hơn.
Trên đây là tổng hợp những kiến thức cơ bản về phương trình parabol cùng những ứng dụng trong đời sống. Mong rằng bạn sẽ vận dụng tốt nhất công thức chúng tôi chia sẻ để giải những bài toán với điểm số trọn vẹn. Cảm ơn các bạn đã quan tâm theo dõi bài viết cùng LabVIETCHEM. Đừng quên cho bài viết của chúng tôi một lượt share trên facebook của bạn nếu thấy bài viết hữu ích nhé!
Từ khóa » Tính Chất Của Parabol
-
Parabol – Wikipedia Tiếng Việt
-
Phương Trình Parabol - Bộ Kiến Thức Hay Nhất Không Thể Bỏ Qua
-
Parabol Là Gì ? Parabol Có Hình Dạng Gì ? Toán Lớp 9, Lớp 10
-
Phương Trình Parabol Có Dạng. Parabol - Tính Chất Và đồ Thị Của Hàm ...
-
Parabol Là Gì? Ứng Dụng Của Parabol Trong Cuộc Sống
-
Phương Trình Parabol Và Các Xác định Tọa độ đỉnh
-
Đường Parabol - Bộ Kiến Thức Hay Nhất Không Thể Bỏ Qua
-
Phương Trình Parabol, Cách Xác định Tọa độ đỉnh ... - DINHNGHIA.VN
-
Sự Tương Giao Giữa đường Thẳng Và Parabol - Toán 9
-
Khái Quát Về Kiến Thức Parabol Trong Đại Số 10 Và Hình Học 10
-
Parabol - Wikimedia Tiếng Việt
-
Lý Thuyết Hàm Số Y = Ax^2 (a ≠ 0) | SGK Toán Lớp 9
-
§5. Parabol (Nâng Cao) - Hoc24