Phương Pháp Dùng Số Phức Tìm Biểu Thức I Hoặc U
Có thể bạn quan tâm
PHƯƠNG PHÁP DÙNG SỐ PHỨC TÌM BIỂU THỨC i HOẶC u
VỚI MÁY CASIO FX-570ES; FX-570ES PLUS;VINACAL-570ES PLUS .
(NHANH VÀ HIỆU QUẢ CHO TRẮC NGHIỆM)
1.Tìm hiểu các đại lượng xoay chiều dạng phức: Xem bảng liên hệ
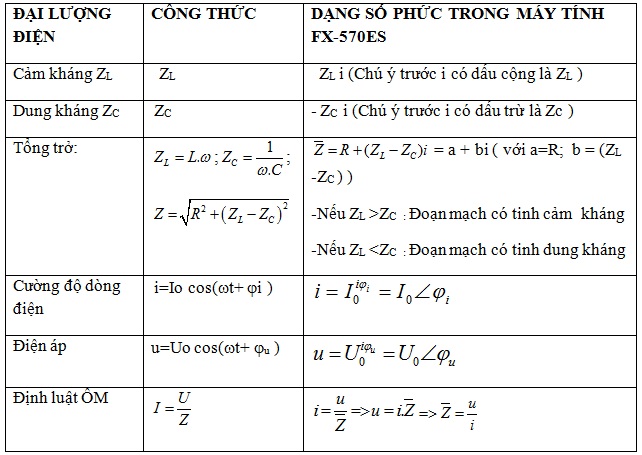
Chú ý: \(\bar{Z}=R+(Z_{L}-Z_{C})i\)( tổng trở phức \(\bar{Z}\) có gạch trên đầu: R là phần thực, (ZL -ZC ) là phần ảo)
Cần phân biệt chữ i sau giá trị b = (ZL -ZC ) là phần ảo , khác với chữ i là cường độ dòng điện
2.Chọn cài dặt máy tính: CASIO fx – 570ES ; 570ES Plus
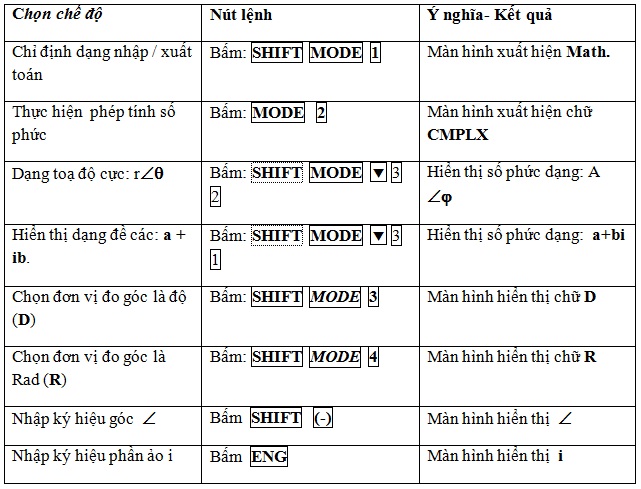
3.Lưu ý Chế độ hiển thị kết quả trên màn hình:

Sau khi nhập, ấn dấu = có thể hiển thị kết quả dưới dạng số vô tỉ,
muốn kết quả dưới dạng thập phân ta ấn SHIFT =
( hoặc nhấn phím S<=>D ) để chuyển đổi kết quả Hiển thị.
4. Các Ví dụ 1:
Ví dụ 1: Mạch điện xoay chiều gồm một điện trở thuần R = 50Ω, một cuộn thuần cảm có hệ số tự cảm \(L=\frac{1}{\pi }(H)\) và một tụ điện có điện dung \(C=\frac{2.10^{-4}}{\pi }(F)\) mắc nối tiếp. Biết rằng dòng điện qua mạch có dạng \(i=5cos100\pi t(A)\) .Viết biểu thức điện áp tức thời giữa hai đầu mạch điện.
Giải : \(Z_{L}=\omega L=100\pi .\frac{1}{\pi }=100\Omega ;Z_{C}=\frac{1}{\omega C}=...=50\Omega\) Và ZL-ZC =50Ω
-Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : dạng hiển thị toạ độ cực:( r\(\angle\)\(\Theta\) )
-Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Ta có :\(u=i.\bar{Z}=I_{0}\angle \varphi _{i}X(R+(Z_{L}-Z_{C}))i=5\angle 0X(50+50i)\) ( Phép NHÂN hai số phức)
Nhập máy: 5 SHIFT (-) 0 X ( 50 + 50 ENG i ) = Hiển thị: 353.55339\(\angle\)45 = 250\(\sqrt{2}\)\(\angle\)45
Vậy biểu thức tức thời điện áp của hai đầu mạch:
u = 250\(\sqrt{2}\) cos( 100πt +π/4) (V).
Ví dụ 2: Một mạch điện xoay chiều RLC không phân nhánh có R = 100Ω; \(C=\frac{1}{\pi }.10^{-4}F;L=\frac{2}{\pi }H\). Cường độ dòng điện qua mạch có dạng: i = 2\(\sqrt{2}\)cos100πt(A). Viết biểu thức điện áp tức thời của hai đầu mạch?
Giải: . \(Z_{L}=\omega L=100\pi .\frac{2}{\pi }=200\Omega ;Z_{C}=\frac{1}{\omega C}=...=100\Omega\)Và ZL-ZC =100Ω
-Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r\(\angle\)\(\Theta\) )
-Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Ta có : \(u=i.\bar{Z}=I_{0}\angle \varphi _{i}X(R+(Z_{L}-Z_{C}))i=2\sqrt{2}\angle 0X(100+100i)\) ( Phép NHÂN hai số phức)
Nhập máy: 2\(\sqrt{2}\) \(\triangleright\) SHIFT (-) 0 X ( 100 + 100 ENG i ) = Hiển thị: 400\(\angle\)45
Vậy biểu thức tức thời điện áp của hai đầu mạch: u = 400cos( 100πt +π/4) (V).
Ví dụ 3: Cho đoạn mạch xoay chiều có R=40Ω, \(L=\frac{1}{\pi }(H),C=\frac{10^{-4}}{0,6\pi }(F)\), mắc nối tiếp điện áp 2 đầu mạch u=100\(\sqrt{2}\)cos100πt (V), Cường độ dòng điện qua mạch là:
A.\(i=2,5cos(100\pi t+\frac{\pi }{4})(A)\) B.\(i=2,5cos(100\pi t-\frac{\pi }{4})(A)\)
C.\(i=2cos(100\pi t-\frac{\pi }{4})(A)\) C.\(i=2cos(100\pi t+\frac{\pi }{4})(A)\)
Giải: \(Z_{L}=\omega L=100\pi .\frac{1}{\pi }=100\Omega ;Z_{C}=\frac{1}{\omega C}=\frac{1}{100\pi .\frac{10^{-4}}{0,6\pi }}=60\Omega\). Và ZL-ZC =40Ω
-Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r\(\angle\)\(\Theta\) )
-Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Ta có : \(i=\frac{u}{\bar{Z}}=\frac{U_{0}\angle \varphi _{u}}{(R+(Z_{L}-Z_{C}))i}=\frac{100\sqrt{2}\angle 0}{(40+40i)}\) ( Phép CHIA hai số phức)
Nhập 100\(\sqrt{2}\) \(\triangleright\) SHIFT (-) 0 : ( 40 + 40 ENG i ) = Hiển thị: 2,5\(\angle\)-45
Vậy : Biểu thức tức thời cường độ dòng điện qua mạch là:
i = 2,5cos(100πt -π/4) (A).
Chọn B
Ví dụ 4: Một đoạn mạch điện gồm điện trở R = 50Ω mắc nối tiếp với cuộn thuần cảm L = 0,5/π (H). Đặt vào hai đầu đoạn mạch một điện áp xoay chiều u = 100\(\sqrt{2}\)cos(100πt- π/4) (V). Biểu thức của cường độ dòng điện qua đoạn mạch là:
A. i = 2cos(100πt- π/2)(A). B. i = 2\(\sqrt{2}\)cos(100πt- π/4) (A).
C. i = 2\(\sqrt{2}\)cos100πt (A). D. i = 2cos100πt (A).
Giải: \(Z_{L}=\omega L=100\pi .\frac{0,5}{\pi }=50\Omega\) Và ZL-ZC =50Ω - 0 = 50Ω
-Với máy FX570ES : Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r\(\angle\)\(\Theta\) )
-Chọn đơn vị đo góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Ta có : \(i=\frac{u}{\bar{Z}}=\frac{U_{0}\angle \varphi _{u}}{(R+Z_{L}i}=\frac{100\sqrt{2}\angle -45}{(50+50i)}\) ( Phép CHIA hai số phức)
Nhập 100\(\sqrt{2}\) \(\triangleright\) SHIFT (-) - 45 : ( 50 + 50 ENG i ) = Hiển thị: 2\(\angle\)- 90
Vậy : Biểu thức tức thời cường độ dòng điện qua mạch là:
i = 2cos( 100πt - π/2) (A).
Chọn A
Ví dụ 5(ĐH 2009): Khi đặt hiệu điện thế không đổi 30V vào hai đầu đoạn mạch gồm điện trở thuần mắc nối tiếp với cuộn cảm thuần có độ tự cảm L = 1/4π (H) thì cường độ dòng điện 1 chiều là 1A. Nếu đặt vào hai đầu đoạn mạch này điện áp u =150\(\sqrt{2}\)cos120πt (V) thì biểu thức cường độ dòng điện trong mạch là:
A.\(i=5\sqrt{2}cos(120\pi t-\frac{\pi }{4})(A)\) B. \(i=5cos(120\pi t+\frac{\pi }{4})(A)\)
C.\(i=5\sqrt{2}cos(120\pi t+\frac{\pi }{4})(A)\) D.\(i=5cos(120\pi t-\frac{\pi }{4})(A)\)
Giải: Khi đặt hiệu điện thế không đổi (hiệu điện thế 1 chiều) thì đoạn mạch chỉ còn có R: R = U/I =30Ω
\(Z_{L}=\omega L=120\pi .\frac{1}{4\pi }=30\Omega;i=\frac{u}{\bar{Z}}=\frac{150\sqrt{2}\angle 0}{(30+30i)}\) ( Phép CHIA hai số phức)
a.Với máy FX570ES :
-Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Bấm SHIFT MODE 3 2 : Cài đặt dạng toạ độ cực:( r\(\angle\)\(\Theta\) )
-Chọn đơn vị góc là độ (D), bấm: SHIFT MODE 3 màn hình hiển thị D
Nhập máy: 150\(\sqrt{2}\) \(\triangleright\) : ( 30 + 30 ENG i ) = Hiển thị: 5\(\angle\)- 45
Vậy: Biểu thức tức thời cường độ dòng điện qua mạch là:
i = 5cos( 120πt - π/4) (A).
Chọn D
b.Với máy FX570ES : -Bấm MODE 2 màn hình xuất hiện: CMPLX.
-Chọn đơn vị góc là độ (R), bấm: SHIFT MODE 4 màn hình hiển thị R
Nhập máy: 150 \(\sqrt{2}\) \(\triangleright\) : ( 30 + 30 ENG i ) = Hiển thị dạng phức: 3.535533..-3.535533…i
Bấm SHIFT 2 3 : Hiển thị: 5\(\angle\) - \(\frac{\pi }{4}\)
Vậy: Biểu thức tức thời cường độ dòng điện qua mạch là:
i = 5cos( 120πt - π/4) (A).
Chọn D
5.TRẮC NGHIỆM:
Câu 1. cho đoạn mạch R, L, C mắc nối tiếp với \(R= 100\Omega , L=\frac{1}{\pi }H, C=\frac{10^{-4}}{2\pi } F\). Đặt điện áp xoay chiều vào giữa hai đầu đoạn mạch \(u_{R,L}= 200\sqrt{2}cos(100\pi t+\frac{\pi }{2})(V)\). biểu thức u có dạng
A. \(u=200cos(100\pi t)V\) B.\(u=200\sqrt{2}cos(100\pi t)V\)
C. \(u=200cos(100\pi t+\frac{\pi }{3})V\) D.\(u=200\sqrt{2}cos(100\pi t+\frac{\pi }{4})V\)
Câu 2. Cho đoạn mạch R, L, C mắc nối tiếp với \(R=59\Omega , L=\frac{1}{\pi }H\). đặt điện áp xoay chiều \(u=U\sqrt{2}cos(100\pi t)V\) vào giữa hai đầu đoạn mạch thì \(u_{L}=100cos(100\pi t+\frac{\pi }{4})\). Biểu thức uc là:
A. uc = 50\(cos(100\pi t-\frac{\pi }{2})\)(V) B . uc= 50\(\sqrt{2}cos(100\pi t-\frac{\pi }{4})\)(V)
C. uc= 50\(cos(100\pi t-\frac{3\pi }{4})\) D. uc = 50\(\sqrt{2}cos(100\pi t-\frac{3\pi }{4})\)
Từ khóa » điện Xoay Chiều Bằng Số Phức
-
Điện áp Hai đầu Mạch Có Dạng UAB=200√2cos(100πt−7π/12)(V). ... Phương Pháp Casio (số Phức Giải điện Xoay Chiều)
-
Phương Pháp - Ứng Dụng Số Phức Vào Giải Toán Dòng điện Xoay Chiều
-
Giải Bài Tập điện Xoay Chiều Phương Pháp Số Phức - Vật Lí Phổ Thông
-
[Vật Lý 12] Điện Xoay Chiều - Phương Pháp Số Phức - YouTube
-
Sử Dụng Phương Pháp Số Phức Giải Bài Toán Điện Xoay Chiều
-
Giải Nhanh điện Xoay Chiều Sử Dụng Số Phức - SlideShare
-
Phương Pháp Số Phức – Dòng điện Xoay Chiều
-
Ứng Dụng Số Phức Vào Giải Toán Dòng điện Xoay Chiều - Tài Liệu Text
-
Lý Thuyết Giải Toán điện Xoay Chiều Bằng Số Phức
-
Giải Toán Điện Xoay Chiều Bằng Số Phức (kết Hợp Sử Dụng Casio ...
-
Giải điện Xoay Chiều Bằng Phương Pháp Số Phức - Thư Viện Vật Lý
-
Sử Dụng Phương Pháp Số Phức để Giải Bài Toán Dòng điện Xoay Chiều
-
Biểu Diễn Số Phức Của Các đại Lượng Mạch Xoay Chiều - Vật Lý 12
-
Tặng Tài Liệu Giải Mạch điện Xoay Chiều Bằng Số Phức Cực Hay