Phương Trình Tích - Chuyên đề Môn Toán Lớp 8

Phương trình tíchChuyên đề môn Toán lớp 8Bài trướcBài sauNâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi. Mua ngay Từ 79.000đ Tìm hiểu thêm

Phương trình tích là phần nội dung quan trọng được học trong chương trình Toán 8 học kì 2. Để giúp các em nắm vững nội dung này, VnDoc gửi tới các bạn Chuyên đề Toán học lớp 8: Phương trình tích. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.

Chuyên đề: Phương trình tích

• A. Lý thuyết
• B. Trắc nghiệm & Tự luận

Để ôn tập hiệu quả dạng bài tập này, mời các bạn tham khảo thêm:

Bài tập Toán lớp 8: Phương trình tích

A. Lý thuyết Toán 8 bài Phương trình tích

1. Phương trình tích và cách giải

Phương trình tích có dạng \(A(x).B(x) = 0\)

Cách giải phương trình tích \(A(x).B(x) = 0\) ⇔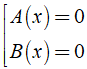

Cách bước giải phương trình tích

Bước 1: Đưa phương trình đã cho về dạng tổng quát \(A(x).B(x) = 0\) bằng cách:

Chuyển tất cả các hạng tử của phương trình về vế trái. Khi đó vế phải bằng 0.

Phân tích đa thức ở vế phải thành nhân tử

Bước 2: Giải phương trình và kết luận

Ví dụ 1: Giải phương trình \((x + 1)(x + 4) = (2 - x)(2 + x)\)

Hướng dẫn:

Ta có: \((x + 1)(x + 4) = (2 - x )( 2 + x )\) ⇔ x2 + 5x + 4 = 4 - x2

⇔ 2x2 + 5x = 0 ⇔ \(x(2x + 5)\) = 0

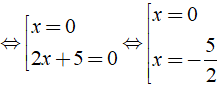
Vậy phương trình đã cho có tập nghiệm là \(S = {- 5/2; 0}\)

Ví dụ 2: Giải phương trình x3 - x2 = 1 - x

Hướng dẫn:

Ta có: x3 - x2 = 1 - x ⇔ x2(x - 1) = - (x - 1)

⇔ x2(x - 1) + (x - 1) = 0 ⇔ (x - 1)(x2 + 1) = 0

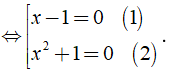
( 1 ) ⇔ x - 1 = 0 ⇔ x = 1.

( 2 ) ⇔ x2 + 1 = 0 (Vô nghiệm vì x2 ≥ 0 ⇒ x2 + 1 ≥ 1)

Vậy phương trình đã cho có tập nghiệm là S = {1}.

B. Trắc nghiệm & Tự luận phương trình tích

I. Bài tập trắc nghiệm

Bài 1: Nghiệm của phương trình (x + 2)(x - 3) = 0 là?

A. x = - 2.

B. x = 3.

C. x = - 2; x = 3 .

D. x = 2.

Ta có: (x + 2)(x - 3) = 0 ⇔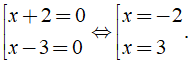

Vậy nghiệm của phương trình là x = - 2; x = 3.

Chọn đáp án C.

Bài 2: Tập nghiệm của phương trình (2x + 1)(2 - 3x) = 0 là?

A. S = {- 1/2}.

B. S = {- 1/2; 3/2}

C. S = {- 1/2; 2/3}.

D. S = {3/2}.

Ta có: (2x + 1)(2 - 3x) = 0 ⇔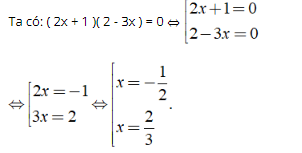

Vậy tập nghiệm của phương trình S = {- 1/2; 2/3}.

Chọn đáp án C.

Bài 3: Nghiệm của phương trình 2x(x + 1) = x2 - 1 là?

A. x = - 1.

B. x = ± 1.

C. x = 1.

D. x = 0.

Ta có: 2x(x + 1) = x2 - 1 ⇔ 2x(x + 1) = (x + 1)(x - 1)

⇔ (x + 1)(2x - x + 1) = 0 ⇔ (x + 1)(x + 1) = 0

⇔ (x + 1)2 = 0 ⇔ x + 1 = 0 ⇔ x = - 1.

Vậy phương trình có nghiệm là x = - 1.

Chọn đáp án A.

Bài 4: Giá trị của m để phương trình (x + 2)(x - m) = 4 có nghiệm x = 2 là?

A. m = 1.

B. m = ± 1.

C. m = 0.

D. m = 2.

Phương trình (x + 2)(x - m) = 4 có nghiệm x = 2, thay x = 2 vào phương trình đã cho

Khi đó ta có: (2 + 2)(2 - m) = 4 ⇔ 4(2 - m) = 4

⇔ 2 - m = 1 ⇔ m = 1.

Vậy m = 1 là giá trị cần tìm.

Chọn đáp án A.

Bài 5: Giá trị của m để phương trình x3 - x2 = x + m có nghiệm x = 0 là?

A. m = 1.

B. m = - 1.

C. m = 0.

D. m = ± 1.

Thay x = 0 vào phương trình x3 - x2 = x + m.

Khi đó ta có: 03 - 02 = 0 + m ⇔ m = 0.

Vậy m = 0 là giá trị cần tìm.

Chọn đáp án C.

Câu 6: Phương trình (x – 1)(x – 2)(x – 3) = 0 có số nghiệm là:

A. 1

B. 2

C. 3

D. 4

Câu 7: Chọn khẳng định đúng.

A. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm trái dấu

B. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm dương

C. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm cùng âm

D. Phương trình 8x(3x – 5) = 6(3x – 5) có một nghiệm duy nhất

Câu 8: Số nghiệm của phương trình: (x2 + 9) (x – 1) = (x2 + 9) (x + 3) là

A. 2

B. 1

C. 0

D. 3

Câu 9: Phương trình: (4 + 2x)(x – 1) = 0 có nghiệm là:

A. x = 1; x = 2

B. x = -2; x = 1

C. x = -1; x = 2

D. x = 1; x = 2

Câu 10: Phương trình (x2 – 1) (x – 2) (x – 3) = 0 có số nghiệm là:

A. 1

B. 2

C. 3

D. 4

Câu 11: Tích các nghiệm của phương trình x3 – 3 x2 – x + 3 = 0 là

A. -3

B. 3

C. -6

D. 6

Câu 12: Cho phương trình 5 – 6(2x – 3) = x(3 – 2x) + 5. Chọn khẳng định đúng.

A. Phương trình có hai nghiệm trái dấu

B. Phương trình có hai nghiệm nguyên

C. Phương trình có hai nghiệm cùng dương

D. Phương trình có một nghiệm duy nhất

Câu 13: Tập nghiệm của phương trình (x2 + x) (x2 + x + 1) = 6 là

A. S = {-1; -2}

B. S = {1; 2}

C. S = {1; -2}

D. S = {-1; 2}

Câu 14: Biết rằng phương trình (4 x2 – 1)2 = 8 x + 1 có nghiệm lớn nhất là x0. Chọn khẳng định đúng

A. x0 = 3

B. x0 < 2

C. x0 > 1

D. x0 < 0

Câu 15: Cho phương trình x4 – 8 x2 + 16 = 0. Chọn khẳng định đúng

A. Phương trình có hai nghiệm đối nhau

B. Phương trình vô nghiệm

C. Phương trình có một nghiệm duy nhất

D. Phương trình có 4 nghiệm phân biệt

II. Bài tập tự luận

Bài 1: Giải các phương trình sau:

a) (5x - 4)(4x + 6) = 0

b) (x - 5)(3 - 2x)(3x + 4) = 0

c) (2x + 1)(x2 + 2) = 0

d) (x - 2)(3x + 5) = (2x - 4)(x + 1)

Hướng dẫn:

a) Ta có: (5x - 4)(4x + 6) = 0

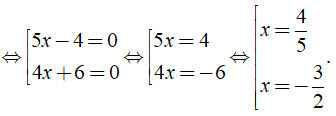
Vậy phương trình đã cho có tập nghiệm là S = {- 3/2; 4/5}.

b) Ta có: (x - 5)(3 - 2x)(3x + 4) = 0

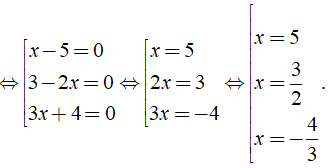
Vậy phương trình đã cho có tập nghiệm là S = {- 4/3; 3/2; 5}.

c) Ta có: (2x + 1)(x2 + 2) = 0

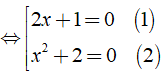
Giải (1) ⇔ 2x + 1 = 0 ⇔ 2x = - 1 ⇔ x = - 1/2.

Ta có: x2 ≥ 0 ⇒ x2 + 2 ≥ 2 ∀ x ∈ R

⇒ Phương trình (2) vô nghiệm.

Vậy phương trình đã cho có tập nghiệm S = {- 1/2}.

d) Ta có: (x - 2)(3x + 5) = (2x - 4 )( x + 1)

⇔ (x - 2)(3x + 5) - 2(x - 2)(x + 1) = 0

⇔ (x - 2)[(3x + 5) - 2(x + 1)] = 0

⇔ (x - 2)(x + 3) = 0

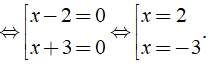
Vậy phương trình đã cho có tập nghiệm là S = {- 3; 2}.

Bài 2: Giải các phương trình sau:

a) (2x + 7)2 = 9(x + 2 )2

b) (x2 - 1)(x + 2)(x - 3) = (x - 1)(x2 - 4)(x + 5)

c) (5x2 - 2x + 10)2 = (x2 + 10x - 8)2

d) (x2 + x)2 + 4(x2 + x) - 12 = 0

Hướng dẫn:

a) Ta có: (2x + 7)2 = 9(x + 2)2

⇔ (2x + 7)2 - 9(x + 2)2 = 0

⇔ [(2x + 7) + 3(x + 2)][(2x + 7) - 3(x + 2)] = 0

⇔ (5x + 13)(1 - x) = 0

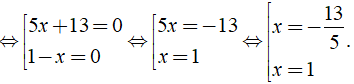
Vậy phương trình đã cho có tập nghiệm là S = {- 13/5; 1}.

b) Ta có: (x2 - 1)(x + 2)(x - 3) = (x - 1)(x2 - 4)(x + 5)

⇔ (x2 - 1)(x + 2)( x - 3) - (x - 1)(x2 - 4 )(x + 5) = 0

⇔ (x - 1)(x + 1)(x + 2)(x - 3) - (x - 1)(x - 2)(x + 2)(x + 5) = 0

⇔ (x - 1)(x + 2)[(x + 1)(x - 3) - (x - 2)(x + 5)] = 0

⇔ (x - 1)(x + 2)[(x2 - 2x - 3) - (x2 + 3x - 10)] = 0

⇔ (x - 1)(x + 2)(7 - 5x) = 0

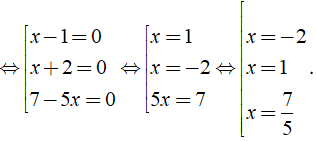
Vậy phương trình có tập nghiệm là S = { - 2; 1; 7/5 }.

c) Ta có: (5x2 - 2x + 10)2 = (3x2 + 10x - 8)2

⇔ (5x2 - 2x + 10)2 - (3x2 + 10x - 8)2 = 0

⇔ [(5x2 - 2x + 10) - (3x2 + 10x - 8)][(5x2 - 2x + 10) + (3x2 + 10x - 8)] = 0

⇔ (2x2 - 12x + 18)(8x2 + 8x + 2) = 0

⇔ 4(x2 - 6x + 9)(4x2 + 4x + 1) = 0

⇔ 4(x - 3)2(2x + 1)2 = 0

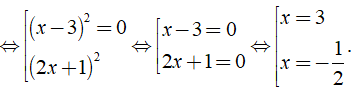
Vậy phương trình đã cho có tập nghiệm S = {- 1/2; 3}.

d) Ta có: (x2 + x)2 + 4(x2 + x) - 12 = 0

Đặt t = x2 + x, khi đó phương trình trở thành:

t2 + 4t - 12 = 0 ⇔ (t + 6)(t - 2) = 0

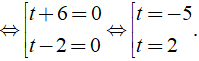
+ Với t = - 6, ta có: x2 + x = - 6 ⇔ x2 + x + 6 = 0 ⇔ (x + 1/2)2 + 23/4 = 0

Mà (x + 1/2)2 + 23/4 ≥ 23/4 ∀ x ∈ R ⇒ Phương trình đó vô nghiệm.

+ Với t = 2, ta có x2 + x = 2 ⇔ x2 + x - 2 = 0

⇔ (x + 2)(x - 1) = 0 ⇔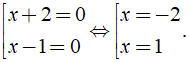

Vậy phương trình có tập nghiệm là S = {- 2;1}.

...................................

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Phương trình tích. Hy vọng đây là tài liệu hữu ích giúp các em nắm vững các dạng toán về Phương trình tích, từ đó nâng cao kỹ năng giải Toán 8 và học tốt môn Toán lớp 8 hơn. 

Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc