Tích Có Hướng Của 2 Vecto Là Gì? Công Thức, định Nghĩa Tính Chất ...

Tích có hướng của 2 vecto là gì? Công thức, định nghĩa tính chất, ứng ụng Bài tập vận dụng!

Tích có hướng của 2 vecto là gì? Công thức, định nghĩa tính chất, ứng ụng

1) Công thức định thức:

$\left| \begin{matrix}   a {} b  \\   c {} d  \\\end{matrix} \right|=ad-bc.$

2) Định nghĩa tích có hướng của 2 vectơ:

Cho 2 vectơ: $\overrightarrow{u}=\left( {{x}_{1}};{{y}_{1}};{{z}_{1}} \right);\,\overrightarrow{v}=\left( {{x}_{2}};{{y}_{2}};{{z}_{2}} \right).$

Khi đó tích có hướng của 2 vectơ $\overrightarrow{u}=\left( {{x}_{1}};{{y}_{1}};{{z}_{1}} \right);\,\overrightarrow{v}=\left( {{x}_{2}};{{y}_{2}};{{z}_{2}} \right)$ký hiệu: $\left[ \overrightarrow{u},\overrightarrow{v} \right]$ là một vectơ và được tính như sau: $\left[ \overrightarrow{u},\overrightarrow{v} \right]=\left( \left| \begin{matrix}   {{y}_{1}} {} {{z}_{1}}  \\   {{y}_{2}} {} {{z}_{2}}  \\\end{matrix} \right|;\left| \begin{matrix}   {{z}_{1}} {} {{x}_{1}}  \\   {{z}_{2}} {} {{x}_{2}}  \\\end{matrix} \right|;\left| \begin{matrix}   {{x}_{1}} {} {{y}_{1}}  \\   {{x}_{2}} {} {{y}_{2}}  \\\end{matrix} \right| \right)=\left( {{y}_{1}}{{z}_{2}}-{{y}_{2}}{{z}_{1}};{{z}_{1}}{{x}_{2}}-{{z}_{2}}{{x}_{1}};{{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}} \right)$

3) Tính chất:

$\left[ \overrightarrow{u},\overrightarrow{v} \right]\bot \overrightarrow{u};\,\,\left[ \overrightarrow{u},\overrightarrow{v} \right]\bot \overrightarrow{v};\,\,\left[ \overrightarrow{u},\overrightarrow{v} \right]=-\left[ \overrightarrow{v},\overrightarrow{u} \right]$

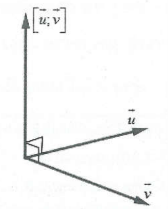
Độ dài của vectơ tích có hướng $\left| \left[ \overrightarrow{u},\overrightarrow{v} \right] \right|=\left| \overrightarrow{u} \right|.\left| \overrightarrow{v} \right|.\sin (\overrightarrow{u},\overrightarrow{v}).$

Hai vectơ $\overrightarrow{u};\,\,\overrightarrow{v}$ cùng phương $\Leftrightarrow \left[ \overrightarrow{u},\overrightarrow{v} \right]=\overrightarrow{0}\,\,(0;0;0).$

Ba vectơ $\overrightarrow{a};\,\,\overrightarrow{b};\,\,\overrightarrow{c}$ đồng phẳng khi $\left[ \overrightarrow{a},\overrightarrow{b} \right].\overrightarrow{c}=0.$

Từ đó suy ra 4 điểm A, B, C, D là 4 đỉnh của một tứ diện khi 3 vectơ $\overrightarrow{AB};\overrightarrow{\,AC};\overrightarrow{\,AD}$ không đồng phẳng hay $\left[ \overrightarrow{AB},\overrightarrow{AC} \right].\overrightarrow{AD}\ne 0$ và 4 điểm A, B, C, D đồng phẳng khi $\left[ \overrightarrow{AB},\overrightarrow{AC} \right].\overrightarrow{AD}=0.$

4) Ứng dụng:

• Diện tích hình bình hành $ABCD:\,\,\,{{S}_{ABCD}}=\left| \left[ \overrightarrow{AB},\overrightarrow{AD} \right] \right|.$
• Diện tích tam giác $ABC:\,\,\,{{S}_{ABC}}=\frac{1}{2}\left| \left[ \overrightarrow{AB},\overrightarrow{AC} \right] \right|.$
• Thể tích khối hộp $ABCD.A'B'C'D':\,\,\,{{V}_{ABCD.A'B'C'D'}}=\left| \left[ \overrightarrow{AB},\overrightarrow{AD} \right].\overrightarrow{AA'} \right|.$
• Thể tích tứ diện ABCD: ${{V}_{ABCD}}=\frac{1}{6}\left| \left[ \overrightarrow{AB},\overrightarrow{AC} \right].\overrightarrow{AD} \right|.$

Luyện bài tập vận dụng tại đây!

Báo lỗi

TOÁN LỚP 12

CHUYÊN ĐỀ 1: HÀM SỐ

• A.1. TÍNH ĐƠN ĐIỆU CỦA HÀM SỐ
• A.2. CỰC TRỊ CỦA HÀM SỐ
• A.3. GTLN VÀ GTNN CỦA HÀM SỐ
• A.4. TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ
• A.5. NHẬN DIỆN ĐỒ THỊ HÀM SỐ
• A.6. BÀI TOÁN BIỆN LUẬN SỐ NGHIỆM PHƯƠNG TRÌNH BẰNG ĐỒ THỊ
• A.7. BÀI TOÁN TƯƠNG GIAO CỦA HAI ĐỒ THỊ HÀM SỐ
• A.8. BÀI TOÁN TIẾP TUYẾN
• A.9. BÀI TOÁN TÌM ĐIỂM TRÊN ĐỒ THỊ HÀM SỐ

CHUYÊN ĐỀ 2: LOGARIT

• B.1. CÔNG THỨC LŨY THỪA
• B.2. CÔNG THỨC LOGARITH
• B.3. HÀM SỐ LŨY THỪA MŨ VÀ LOGARITH
• B.4. PHƯƠNG TRÌNH MŨ
• B.5. PHƯƠNG TRÌNH LOGA
• B.6. BẤT PHƯƠNG TRÌNH MŨ
• B.7. BẤT PHƯƠNG TRÌNH LOGARITH
• B.8. BÀI TOÁN VỀ LÃI SUẤT TĂNG TRƯỞNG
• B.9. BÀI TOÁN VỀ MIN-MAX LOGA

CHUYÊN ĐỀ 3: TÍCH PHÂN

• C.1. MỞ ĐẦU VỀ NGUYÊN HÀM
• C.2. PHƯƠNG PHÁP VI PHÂN TÌM NGUYÊN HÀM
• C.3. PHƯƠNG PHÁP ĐỔI BIẾN SỐ TÌM NGUYÊN HÀM
• C.4. PHƯƠNG PHÁP TỪNG PHẦN TÌM NGUYÊN HÀM
• C.5. NGUYÊN HÀM CỦA HÀM PHÂN THỨC HỮU TỈ
• C.6. NGUYÊN HÀM CỦA HÀM SỐ LƯỢNG GIÁC
• C.7. CÁC CÔNG THỨC CƠ BẢN VỀ TÍCH PHÂN
• C.8. PHƯƠNG PHÁP ĐỔI BIẾN SỐ TÍNH TÍCH PHÂN
• C.9. PHƯƠNG PHÁP TỪNG PHẦN TÍNH TÍCH PHÂN
• C.10. TÍCH PHÂN HÀM HỮU TỈ VÀ LƯỢNG GIÁC
• C.11. MỘT SỐ DẠNG TÍCH PHÂN ĐẶC BIỆT VÀ NÂNG CAO
• C.12. ỨNG DỤNG CỦA TÍCH PHÂN TÍNH DIỆN TÍCH HÌNH PHẲNG
• C.13. ỨNG DỤNG CỦA TÍCH PHÂN TÍNH THỂ TÍCH KHỐI TRÒN XOAY
• C.14. MỘT SỐ ỨNG DỤNG KHÁC CỦA TÍCH PHÂN
• C.15. MỘT SỐ BÀI TOÁN CHỌN LỌC VÀ NÂNG CAO VỀ TÍCH PHÂN

CHUYÊN ĐỀ 4: SỐ PHỨC

• D.1. CÁCH TÍNH TOÁN CƠ BẢN VỚI SỐ PHỨC
• D.2. PHƯƠNG TRÌNH PHỨC
• D.3. QUỸ TÍCH PHỨC
• D.4. CỰC TRỊ SỐ PHỨC (NÂNG CAO)

CHUYÊN ĐỀ 5: HÌNH HỌC KHÔNG GIAN

• E.1. ĐẠI CƯƠNG VỀ HÌNH HỌC KHÔNG GIAN
• E.2. QUAN HỆ SONG SONG
• E.3. VECTO TRONG KHÔNG GIAN
• E.4. QUAN HỆ VUÔNG GÓC
• E.5. BÀI TOÁN VỀ GÓC
• E.6. BÀI TOÁN VỀ KHOẢNG CÁCH
• E.7. THỂ TÍCH KHỐI CHÓP
• E.8. TỈ SỐ THỂ TÍCH KHỐI ĐA DIỆN
• E.9. MẶT CẦU HÌNH CẦU KHỐI CẦU
• E.10. MẶT TRỤ HÌNH TRỤ KHỐI TRỤ
• E.11. MẶT NÓN HÌNH NÓN KHỐI NÓN
• E.12. BÀI TOÁN CỰC TRỊ HÌNH KHÔNG GIAN
• E.13. BÀI TOÁN THỰC TẾ HÌNH KHÔNG GIAN

CHUYÊN ĐỀ 6: HÌNH HỌC TỌA ĐỘ

• F.1. TỌA ĐỘ ĐIỂM VECTOR
• F.2. TÍCH CÓ HƯỚNG CỦA HAI VECTOR
• F.3. PT MẶT PHẲNG ĐƯỜNG THẲNG MẶT CẦU
• F.4. BÀI TOÁN VỊ TRÍ TƯƠNG ĐỐI GÓC KHOẢNG CÁCH
• F.5. CÁC DẠNG VIẾT PT MẶT PHẲNG
• F.6. CÁC DẠNG VIẾT PT ĐƯỜNG THẲNG
• F.7. BÀI TOÁN VỀ PHƯƠNG TRÌNH MẶT CẦU
• F.8. BÀI TOÁN TÌM ĐIỂM TRONG TỌA ĐỘ KHÔNG GIAN
• F.9. BÀI TOÁN VỀ CỰC TRỊ TỌA ĐỘ TRONG KHÔNG GIAN

× Close

báo lỗi

Vấn đề em gặp phải là gì? Sai nội dung Lý thuyết khó hiểu Nội dung chưa phù hợp (VD: Đã giảm tải, ...) Lỗi khác

Hãy viết chi tiết giúp Tự Học 365

Gửi Hủy bỏ

×

Đăng ký

Năm sinh 20012002200320042005200620072008200920102011201220132014201520162017201820192020 hoặc Đăng nhập nhanh bằng: (*) Khi bấm vào đăng ký tài khoản, bạn chắc chắn đã đoc và đồng ý với Chính sách bảo mật và Điều khoản dịch vụ của Tự Học 365.