Tìm 1 CSN Có 4 Số Hạng Biết Tổng Của Chúng Bằng 15 Và Tổng Các ...

Học liệu Hỏi đáp Đăng nhập Đăng ký

• Học bài
• Hỏi bài
• Kiểm tra
• ĐGNL
• Thi đấu
• Bài viết Cuộc thi Tin tức Blog học tập
• Trợ giúp
• Về OLM

Chọn lớp Tất cả Mẫu giáo Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 ĐH - CĐ Chọn môn Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên Cập nhật Hủy Cập nhật Hủy

• Mẫu giáo
• Lớp 1
• Lớp 2
• Lớp 3
• Lớp 4
• Lớp 5
• Lớp 6
• Lớp 7
• Lớp 8
• Lớp 9
• Lớp 10
• Lớp 11
• Lớp 12
• ĐH - CĐ

K Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp Tất cả Mẫu giáo Lớp 1 Lớp 2 Lớp 3 Lớp 4 Lớp 5 Lớp 6 Lớp 7 Lớp 8 Lớp 9 Lớp 10 Lớp 11 Lớp 12 ĐH - CĐ Chọn môn Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên Tạo câu hỏi Hủy Xác nhận câu hỏi phù hợp

×

Chọn môn học Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên Mua vip

• Tất cả
• Mới nhất
• Câu hỏi hay
• Chưa trả lời
• Câu hỏi vip

CG Charlotte Grace 17 tháng 4 2021

Tìm 1 CSN có 4 số hạng biết tổng của chúng bằng 15 và tổng các bình phương của chúng bằng 85

#Toán lớp 11 1 NV Nguyễn Việt Lâm Giáo viên 17 tháng 4 2021

Gọi các số hạng của CSN là \(u_1;u_1q;u_1q^2;u_1q^3\)

\(\Rightarrow\left\{{}\begin{matrix}u_1\left(1+q+q^2+q^3\right)=15\\u_1^2\left(1+q^2+q^4+q^6\right)=85\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u_1^2\left(q+1\right)^2\left(q^2+1\right)^2=225\\u_1^2\left(q^2+1\right)\left(q^4+1\right)=85\end{matrix}\right.\)

\(\Rightarrow\dfrac{\left(q+1\right)^2\left(q^2+1\right)}{q^4+1}=\dfrac{45}{17}\)

\(\Leftrightarrow14q^4-17q^3-17q^2-17q+14=0\)

Với \(q=0\) ko phải nghiệm, với \(q\ne0\)

\(\Leftrightarrow14\left(q^2+\dfrac{1}{q^2}\right)-17\left(q+\dfrac{1}{q}\right)-17=0\)

\(\Leftrightarrow14\left(q+\dfrac{1}{q}\right)^2-17\left(q+\dfrac{1}{q}\right)-45=0\Rightarrow\left[{}\begin{matrix}q+\dfrac{1}{q}=-\dfrac{9}{7}\\q+\dfrac{1}{q}=\dfrac{5}{2}\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}7q^2+9q+7=0\\2q^2-5q+2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}q=2\\q=\dfrac{1}{2}\end{matrix}\right.\)

\(\Rightarrow u_1=\dfrac{15}{1+q+q^2+q^3}=...\)

Đúng(1) QH Quang Huy Đặng 31 tháng 10 2023

đoạn cuối là sao vậy ạ

Đúng(0) Các câu hỏi dưới đây có thể giống với câu hỏi trên T títtt 16 tháng 9 2023

tìm 3 số hạng liên tiếp của 1 cấp số cộng biết tổng của chúng bằng 12 và tổng các bình phương của chúng bằng 66

#Toán lớp 11 2 AH Akai Haruma Giáo viên 16 tháng 9 2023

Lời giải:

Gọi số hạng đầu tiên là $a$ và công sai $d$. Khi đó số hạng thứ 2 và 3 lần lượt là $a+d, a+2d$

Theo bài ra ta có:

$a+(a+d)+(a+2d)=12$

$\Rightarrow a+d=4$

$a^2+(a+d)^2+(a+2d)^2=66$

$\Leftrightarrow 3a^2+5d^2+6ad=66$

$\Leftrightarrow 3(4-d)^2+5d^2+6(4-d)d=66$

$\Leftrightarrow 2d^2-18=0$

$\Leftrightarrow d=\pm 3$

Nếu $d=3$ thì $a=1$. Khi đó 3 số cần tìm là $1,4, 7$

Nếu $d=-3$ thì $a=7$. Khi đó 3 số cần tìm là $7, 4, 1$

Đúng(0) ND Nguyễn Đức Trí 16 tháng 9 2023

\(S_3=\dfrac{3\left[2u_1+2d\right]}{2}\)

\(\Leftrightarrow2u_1+2d=\dfrac{2S_3}{3}\)

\(\Leftrightarrow2\left(u_1+d\right)=\dfrac{2S_3}{3}\)

\(\Leftrightarrow u_1+d=\dfrac{S_3}{3}=\dfrac{12}{3}=4\)

\(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_2=4\\u_3=7\end{matrix}\right.\)

mà \(u_1^2+u_2^2+u_3^2=1^2+4^2+7^2=66\) (thỏa đề bài)

Vậy 3 số hạng liên tiếp của 1 cấp số cộng là : \(1;4;7\)

Đúng(0) Xem thêm câu trả lời PT Pham Trong Bach 8 tháng 11 2017 Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tìm số hạng đầu tiên và số hạng thứ tư của dãy ? A. 1;7 B. 2;8 C.2;10...Đọc tiếp

Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20và tổng các bình phương của chúng bằng 120. Tìm số hạng đầu tiên và số hạng thứ tư của dãy ?

A. 1;7

B. 2;8

C.2;10

D.3;9

#Toán lớp 11 1 CM Cao Minh Tâm 8 tháng 11 2017

Đáp án B

Đúng(0) PT Pham Trong Bach 29 tháng 4 2017 Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. A. 1,5,6,8 B. 2,4,6,8 C. 1,4,6,9 D....Đọc tiếp

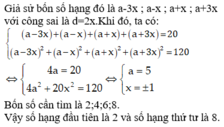
Tìm bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120.

A. 1,5,6,8

B. 2,4,6,8

C. 1,4,6,9

D. 1,4,7,8

#Toán lớp 11 1 CM Cao Minh Tâm 29 tháng 4 2017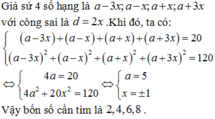

Chọn đáp án B

Đúng(0) PT Pham Trong Bach 9 tháng 5 2017

Bốn số hạng liên tiếp của một cấp số cộng biết tổng của chúng bằng 20 và tổng các bình phương của chúng bằng 120. Tính tổng của hai số hạng đầu tiên?

A. 6

B. 7

C. 5

D. 8

#Toán lớp 11 1 CM Cao Minh Tâm 9 tháng 5 2017

Chọn A

Giả sử bốn số hạng đó là a − 3 x ; a − x ; a + x ; a + 3 x với công sai là d =2x. Khi đó, ta có:

a − 3 x + a − x + a + x + a + 3 x = 20 a − 3 x 2 + a − x 2 + a + x 2 + a + 3 x 2 = 120

⇔ 4 a = 20 4 a 2 + 20 x 2 = 120 ⇔ a = 5 x = ± 1

Vậy bốn số cần tìm là 2; 4; 6; 8.

Tổng của 2 số hạng đầu tiên là:2+ 4= 6.

Đúng(0) PT Pham Trong Bach 20 tháng 1 2018

Ba số hạng liên tiếp của một cấp số cộng có tổng bằng -9 và tổng các bình phương của chúng bằng 29. Tìm số hạng đầu tiên

A. -3 hoặc – 6

B. – 4 hoặc -2

C. -1 hoặc -5

D. -4 hoặc - 7

#Toán lớp 11 1 CM Cao Minh Tâm 20 tháng 1 2018

Chọn B

Gọi ba số hạng liên tiếp của cấp số cộng là a - 2x; a ; a+2x với công sai d=2x.

Theo giả thiết ta có:

a − 2 x + a + a + 2 x = − 9 ( a - 2 x ) 2 + a 2 + a + 2 x 2 = 29 ⇔ 3 a = − 9 3 a 2 + ​ 8 x 2 = 29 ⇔ a = − 3 8 x 2 = 2 ⇔ a = − 3 x = ± 1 2

với

x =    1 2     ⇒ u 1 =    a − 2 x =    − 3 − 2.    1 2 =   − 4

với

x =    − 1 2     ⇒ u 1 =    a − 2 x =    − 3 − 2.    − 1 2 =   − 2

Vậy số hạng đầu tiên là -4 hoặc -2

Đúng(0) PT Pham Trong Bach 8 tháng 3 2019

Tìm một cấp số cộng tăng, biết rằng tổng ba số hạng đầu của nó bằng 27 và tổng các bình phương của chúng bằng 275.

#Toán lớp 11 1 CM Cao Minh Tâm 8 tháng 3 2019

Gọi công sai của cấp số cộng là d; số hạng đầu là u1 = x - d, u2 = x, u3 = x + d.

CSC tăng nên d > 0.

Theo giả thiết, ta có hệ:

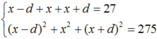
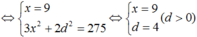
Vậy cấp số cộng cần tìm là : 5, 9, 13 .

Đúng(0) PT Pham Trong Bach 23 tháng 12 2018 Cho bốn số hạng liên tiếp của một cấp số cộng, có tổng của chúng bằng 16 và tổng bình phương của chúng bằng 84. Tính tổng hai bình phương số hạng đầu và số hạng cuối của bốn số hạng đó. A. 34 B. 64 C. 50 D....Đọc tiếp

Cho bốn số hạng liên tiếp của một cấp số cộng, có tổng của chúng bằng 16 và tổng bình phương của chúng bằng 84. Tính tổng hai bình phương số hạng đầu và số hạng cuối của bốn số hạng đó.

A. 34

B. 64

C. 50

D. 49

#Toán lớp 11 1 CM Cao Minh Tâm 23 tháng 12 2018

Đáp án C

Gọi d = 2 x là công sai

ta có bốn số là a - 3 x , a - x , a + x , a + 3 x

Khi đó, từ giả thiết ta có:

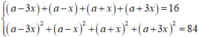
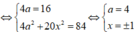
⇔ 1 , 3 , 5 , 7 7 , 5 , 3 , 1

Tổng bình phương của số hạng đầu và cuối là 1 2 + 7 2 = 50

Đúng(0) PT Pham Trong Bach 14 tháng 5 2018

Tìm công sai dương của cấp số cộng ba số hạng, biết tổng của chúng bằng 9 và tổng bình phương bằng 125.

A. 7

B. 8

C. 9

D. 10

#Toán lớp 11 1 CM Cao Minh Tâm 14 tháng 5 2018

Chọn A

Gọi d là công sai. Ba số phải tìm là: (x-d); x; (x+d). Ta có hệ phương trình

Đúng(0) PT Pham Trong Bach 14 tháng 12 2018

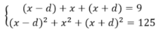
Cho 4 số lập phương thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :

A. 22

B. 166

C. 1752

D. 1408

#Toán lớp 11 1 CM Cao Minh Tâm 14 tháng 12 2018

Gọi 4 số lập thành cấp số cộng là u1,u2,u3,u4

Ta có:

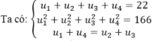
Vậy 4 số đó là 1,4,7,10 hoặc 10,7,4,1

Tổng các lập phương của chúng: 13+43+73+ 103=1408

Đáp án là D

Đúng(0) Xếp hạng Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên

• Tuần
• Tháng
• Năm

• DH Đỗ Hoàn VIP 60 GP
• NT Nguyễn Tuấn Tú 41 GP
• NG Nguyễn Gia Bảo 26 GP
• 1 14456125 17 GP
• VN vh ng 16 GP
• N ngannek 10 GP
• TN Trương Nguyễn Anh Thư 10 GP
• H Hbth 8 GP
• LN Lê Như Bảo Nam 6 GP
• TT tran trong 4 GP

Học liệu Hỏi đáp Link rút gọn Link rút gọn Để sau Đăng ký

Các khóa học có thể bạn quan tâm

× Mua khóa học Tổng thanh toán: 0đ (Tiết kiệm: 0đ) Tới giỏ hàng Đóng ×

Yêu cầu VIP

×

Học liệu này đang bị hạn chế, chỉ dành cho tài khoản VIP cá nhân, vui lòng nhấn vào đây để nâng cấp tài khoản.