Trong Khoảng ( 0;dpi 2 ) Hai Hàm Số Nào Sau đây Cùng đồng Biến?

Trang chủ » Khoảng Từ 0 đến Pi/2 » Trong Khoảng ( 0;dpi 2 ) Hai Hàm Số Nào Sau đây Cùng đồng Biến?

Có thể bạn quan tâm

LUYỆN TẬP TRẮC NGHIỆM 50000+ CÂU HỎI

DÀNH CHO MỌI LỚP 6 ĐẾN 12

TRUY CẬP NGAY XEM CHI TIẾT Trong khoảng ( 0;dpi 2 ) hai hàm số nào sau đây cùng đồng biến? Trong khoảng ( 0;dpi 2 ) hai hàm số nào sau đây cùng đồng biến?

Câu hỏi

Nhận biết

Trong khoảng \(\left( {0;\dfrac{\pi }{2}} \right)\), hai hàm số nào sau đây cùng đồng biến?

A. \(y = \sin x\) và \(y = \cos x\) B. \(y = \sin x\) và \(y = \tan x\) C. \(y = \sin x\) và \(y = \cot x\) . D. \(y = \cos x\) và \(y = \cot x\).

Đáp án đúng: B

Lời giải của Tự Học 365

Giải chi tiết:

Kiểm tra tính đơn điệu của các hàm số: \(y = \sin x,y = \cos x,y = \cot x,y = \tan x\).

Sử dụng máy tính MODE 7:

Start: 0

End: \(\dfrac{\pi }{2}\)

Step: \(\dfrac{\pi }{2}:19\)

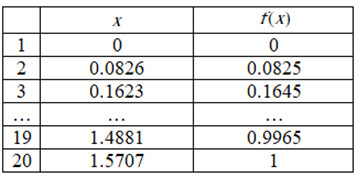
\( \to \) Nhận thấy các giá trị cột \(f\left( x \right)\) luôn tăng.

\( \to \) Hàm số \(y = \sin x\) luôn đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\).

Làm tương tự với các hàm số Thấy có thêm hàm số là hàm đồng biến.

Chọn B.

Ý kiến của bạn Hủy

Δ

Luyện tập

Câu hỏi liên quan

  • Phương trình có 1 họ nghiệm

    Chi tiết
  • x = pi/2 + k2 pi x = p

    Chi tiết
  • Phương trình có 2 họ nghiệm là: x = pi +kpi; x = k2pi/3

    Chi tiết
  • Phương trình có 1 họ nghiệm

    Chi tiết
  • #VALUE!

    Chi tiết
  • Phương trình có 1 họ nghiệm

    Chi tiết
  • (x = pi  6 + kpi 3;x = pi 

    Chi tiết
  • Phương trình có 1 họ nghiệm

    Chi tiết
  • Phương trình có 1 họ nghiệm

    Chi tiết
  • x = kpi; x = pi/3 + k2pi/3

    Chi tiết

Đăng ký

Năm sinh 20012002200320042005200620072008200920102011201220132014201520162017201820192020 hoặc Đăng nhập nhanh bằng: đăng nhập bằng google (*) Khi bấm vào đăng ký tài khoản, bạn chắc chắn đã đoc và đồng ý với Chính sách bảo mật và Điều khoản dịch vụ của Tự Học 365.

Từ khóa » Khoảng Từ 0 đến Pi/2